线性代数亡羊补牢

零基础，学线代，绩点过3不是梦！！

原理

如果矩阵的秩小于n，则矩阵不可逆，否则可逆

逆序数：逆序对数量
行列式符号：分别求行、列的逆序数，和偶正奇负
行列式变换：对应成比例，值为0，交换行/列添负号
上三角：

\[\left|\begin {array}{c} a_{11}&a_{12}&a_{13} \\ 0&a_{22}&a_{23} \\ 0&0&a_{33} \\ \end{array}\right| =a_{11}a_{22}a_{33} \]

行列式展开：余子式 \(M_{ij}\)，代数余子式 \(A_{ij}=(-1)^{i+j}M_{ij}\)

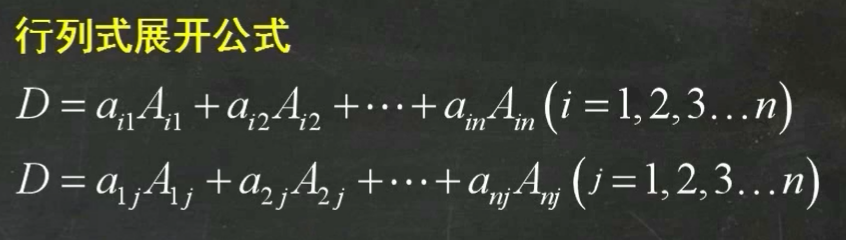
定理：

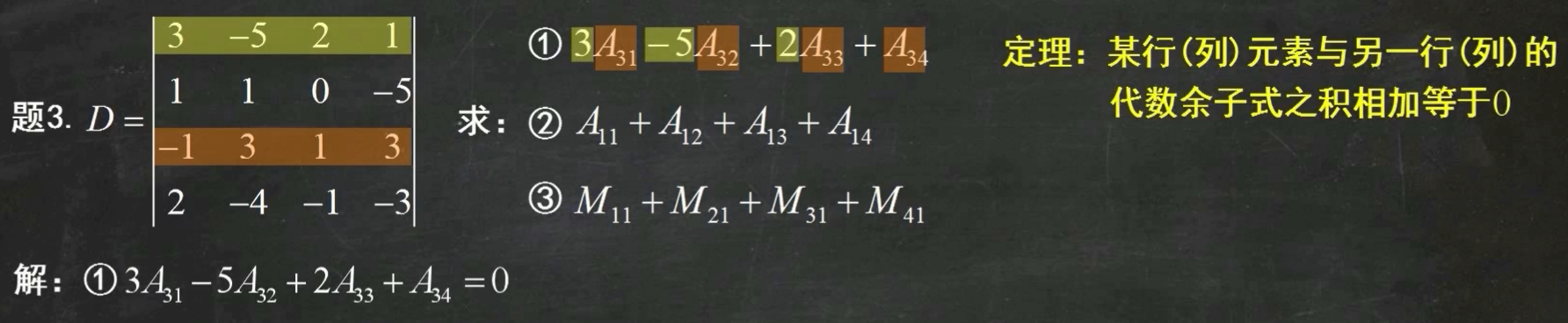
范德蒙行列式：

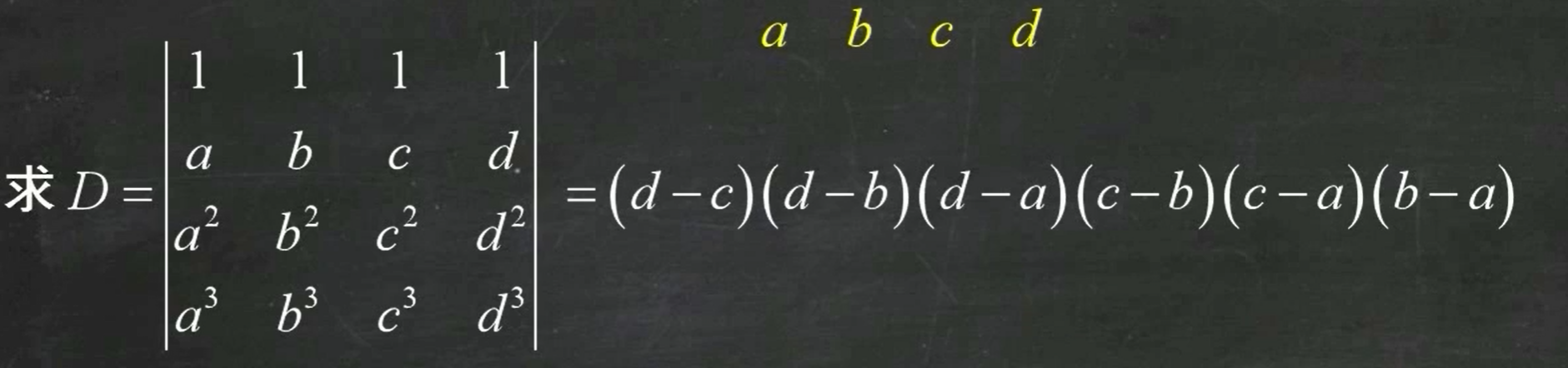
矩阵：\(\lambda A\) 是把矩阵里每个元素乘 \(\lambda\)
乘法：前行乘后列

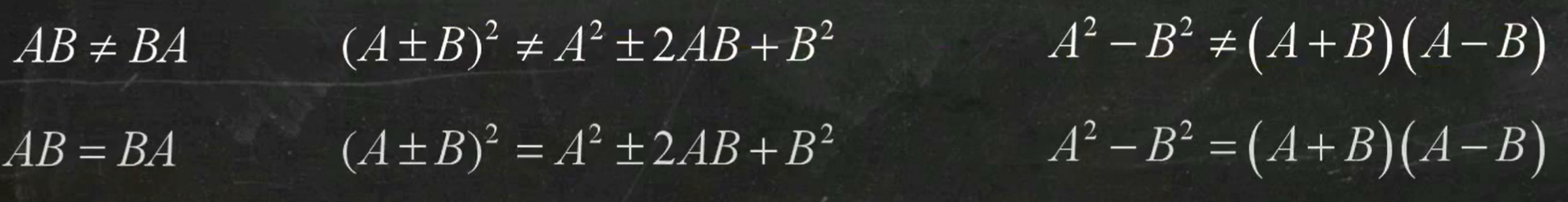
矩阵转置 \(A^T\)：行变列，列变行。
伴随矩阵，单位矩阵，逆矩阵

常用性质：

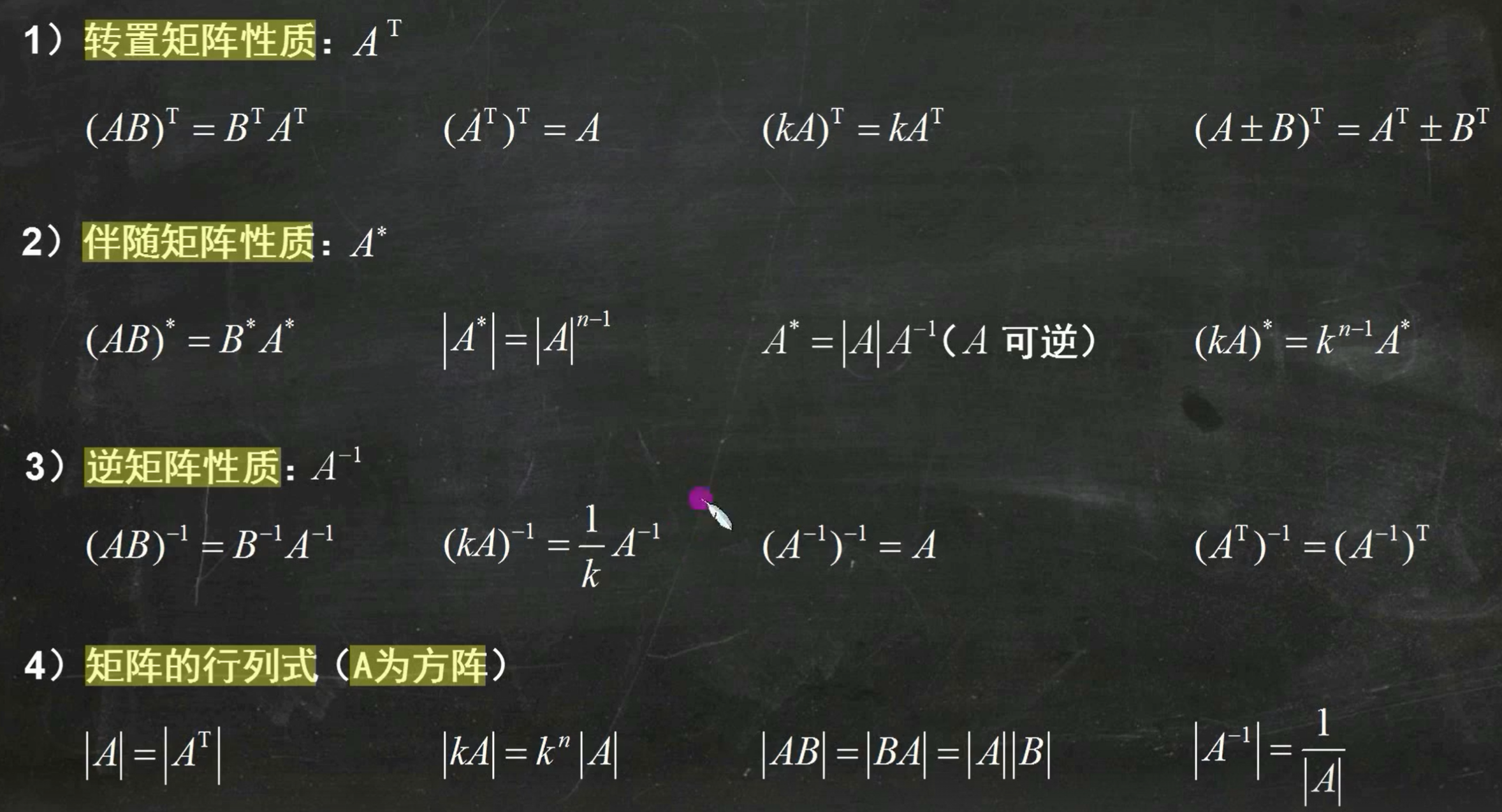
矩阵初等行变换：换行，倍乘，倍加
阶梯形：阶梯首项为主元，阶梯形不唯一
最简形：主元为1，主元所在列其他为0，最简形唯一
求逆矩阵：

二阶求逆公式：

矩阵的秩=主元个数

秩的性质：

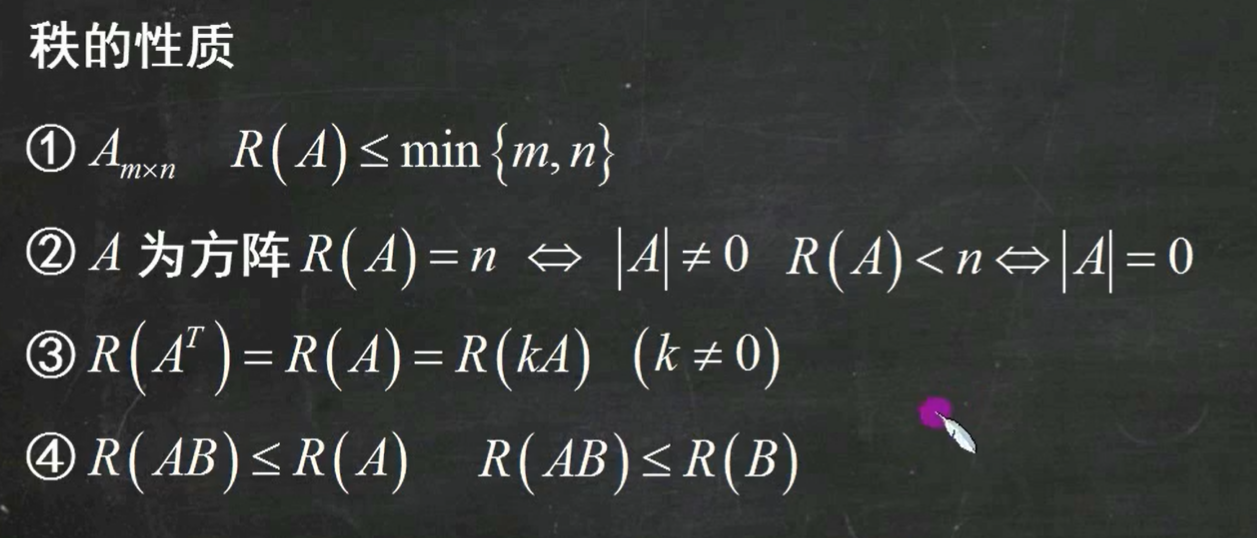
线性相关：

线性表示：化为最简，对应系数

解齐次/非齐次线性方程

解向量记得加T！！！！！！！！

特征值：\(|A-\lambda E|=0\rightarrow \lambda\)
特征向量：\((A-\lambda_i E)x=0\) 的基础解系

相似对角化：

正交化：不同特征值下的向量肯定正交，同一特征值下的向量用施密特正交化计算

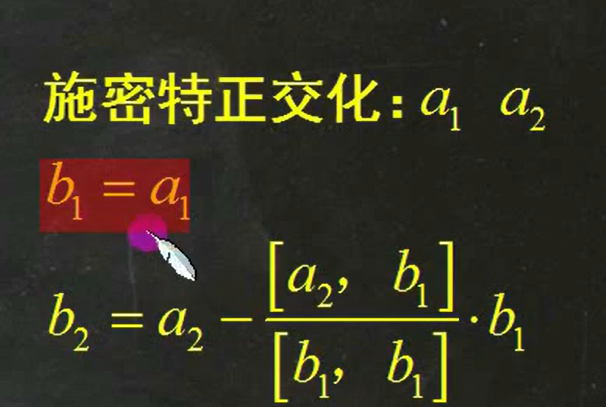
单位化：除以模长

特征值性质：

求特征值用行列式展开！！

二次型矩阵：除2对称分布

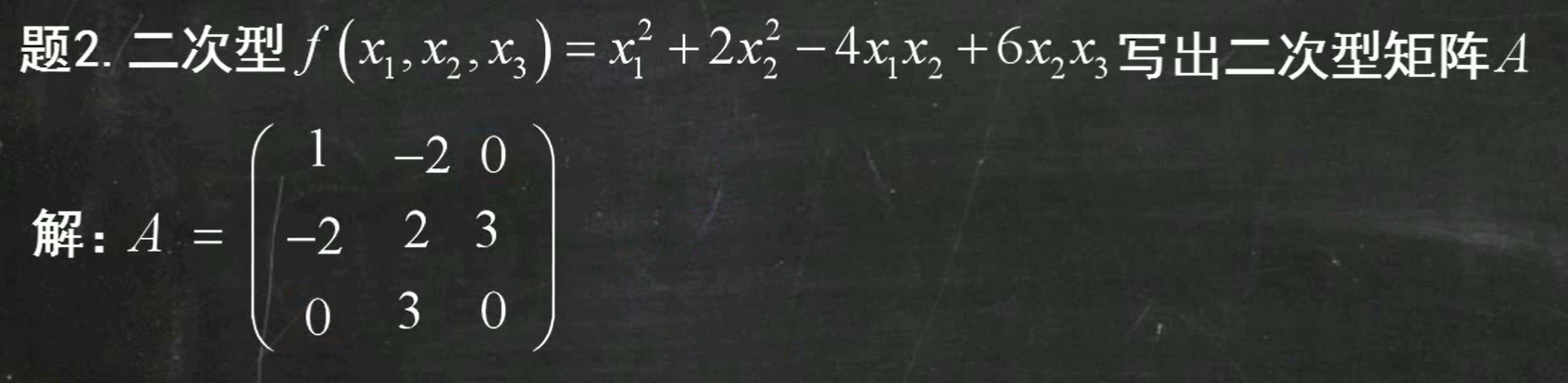
标准型：系数为特征值；正定：系数全大于0；规范型：仅表示符号

顺序主子式：顺下来都大于0

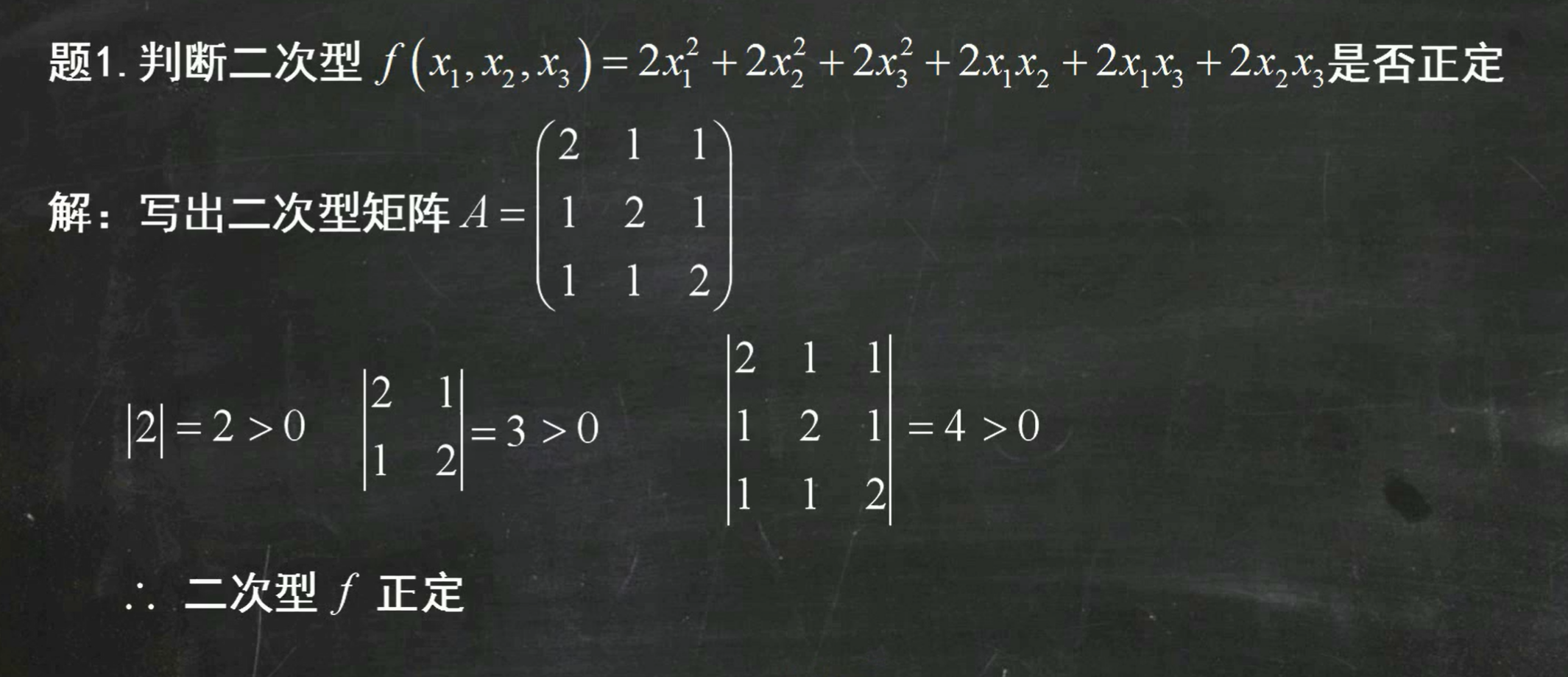
典例

同列元素之和相同

例：

\[\left|\begin {array}{c} 3&1&1&1 \\ 1&3&1&1 \\ 1&1&3&1 \\ 1&1&1&3 \\ \end{array}\right| \]

①将所有行加到第一行
②提取公因子
③用第一行去消其他行

箭型

例：

利用列加减把第一列消为0

行列式展开技巧

化成A一行/列的和形式然后替换原行列式的值，计算值

习题

成比例 + 交换行列

同列元素和相同型

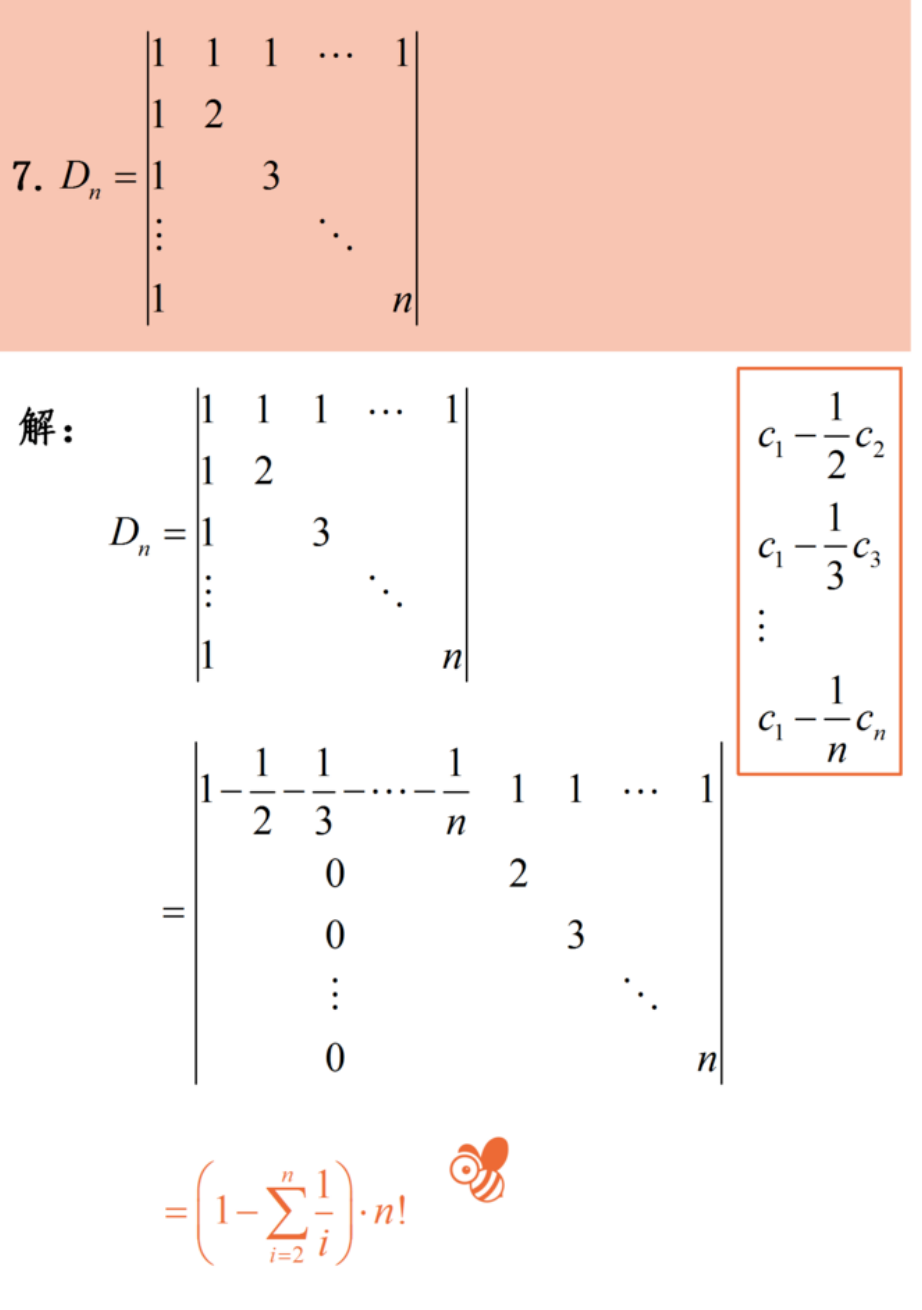
箭型

经典求逆矩阵

先代值再乘

矩阵行列变化性质