Discrete_Mathematics_and_Its_Applications

Discrete_Mathematics_and_Its_Applications

Counting

The Basics of Counting

The product rule 乘法原理
The sum rule 加法原理
The subtraction rule：a ∨ b = a + b - a ∧ b
The division rule: There are n/d ways to do a task if it can be done using a procedure that can be carried out in n ways, and for every way w, exactly d of the n ways correspond to way w.
As in Example 20 in the textbook, page 394 in pdf.
Counting problems can be solved using tree diagrams.

The Pigeonhole Principle

Basic：$> k $(k>0) objects are placed into \(k\) boxes, then there is at least one box containing \(\geq2\) objects.

The generalized pigeonhole principle: If N objects are placed into k
boxes, then there is at least one box containing at least ⌈N/k⌉ objects.

Reverse minimum: (m - 1) * k + 1
Elegant applications: …
Subsequence: （可不连续）子序列
Theorem: Every sequence of \(n^2+1\) distinct real numbers contains a subsequence of length n+1 that is either strictly increasing or strictly
decreasing.

The Ramsey number R(m, n)(\(m,n>1\)): denotes the minimum number of people at a party such that there are either m mutual friends or n mutual enemies,assuming that every pair of people at the party are friends or enemies.

Permutations and Combinations

r-permutations of a set with n distinct elements（\(n\geq r\)）:
P(n, r) = n! / (n - r)!

The number of r-combinations of a set with n elements（0 ≤ r ≤ n）, equals C(n, r) = n! / (r!(n − r)!).
C(n, r) = C(n, n − r).

double counting proofs：A combinatorial proof of an identity is a proof that uses counting arguments to prove that both sides of the identity count the same objects but in different ways.

bijective proofs：a proof that is based on showing that
there is a bijection between the sets of objects counted by the two sides of the identity.

Binomial Coefficient 二项式系数

\[(x+y)^n=\sum_{j=0}^{n}\binom{n}{j}x^{n-j}y^j\\ \sum_{k=0}^{n}\binom{n}{k}=(1+1)^n=2^n \\ \sum_{k=0}^{n}(-1)^k\binom{n}{k}=(-1+1)^n=0 \\ \sum_{k=0}^{n}2^k\binom{n}{k}=(2+1)^n=3^n \\ \text{Pascal’s identity:} \binom{n+1}{k}=\binom{n}{k-1}+\binom{n}{k},\text{So Pascal’s triangle.}\\ \text{Vandermonde’s identity:} \binom{m+n}{r}=\sum_{k=0}^{r}\binom{m}{rk}\binom{n}{k} \binom{2n}{n}=\sum_{k=0}^{n}\binom{n}{n-k}\binom{n} {k}=\sum_{k=0}^{n}\binom{n}{k}^2 \\ \binom{n+1}{r+1}=\sum_{j=r}^{n}\binom{j}{r}\\ \text{Prove by combinatorial argument: Use choosing subset, use bit string.} \]

Generalized Permutations and Combinations

There are C(n + r − 1, r) = C(n + r − 1, n − 1) r-combinations from a set with n elements when repetition of elements is allowed.
Proved by stars and bars.

P426 Counting solutions to equation

The number of different permutations of n objects, where there are n_1 indistinguishable objects of type 1, n_2 indistinguishable objects of type
2, … , and n_k indistinguishable objects of type k, is

\[\frac{n!}{n_1!n_2! ···n_k!} = \frac{A(n,n)}{A(n_1,n_1)A(n_2,n_2)...A(n_k,n_k)}. \]

P427 Word letter reordering
n Distinguishable objects and k distinguishable boxes: \(\frac{n!}{n_1!n_2!···n_k!}\)
n Indistinguishable objects and k distinguishable boxes: C(k + n - 1, n).

Distinguishable objects and indistinguishable boxes: Can enumerate by n into m, … , but no simple closed formula.
Stirling numbers of the second kind: S(n, j) denote the number of ways to distribute n distinguishable objects into j indistinguishable boxes so
that no box is empty.
Then the number of ways to distribute n distinguishable objects into k indistinguishable boxes equals \(\sum_{j=1}^{k}S(n,j)\).

\[S(n,j)=\frac{1}{j!}\sum_{i=0}{j-1}(-1)^i\binom{j}{i}(j-i)^n \]

Indistinguishable objects and indistinguishable boxes: List partition by decreasing order.
If p_k(n) is the number of partitions of n into at most k positive integers,then there are p_k(n) ways to distribute n indistinguishable objects into
k indistinguishable boxes.

Generating Permutations and Combinations

Generating permutations: Lexicographic.
Next permutation: Find last pair such that (a_j, put minimum of a_{j+1},…, a_n that is greater than a_j at a_j, and list remaining in increasing
order.
Generating subsets: Use bit string.
Generating r-combinations: Lexicographic.
Next permutation of {1, 2, … , n}: Find last a_i such that a_i{\ne}n-r+i,
replace a_i with a_i+1, a_j with a_i+j-i+1 (increasing from a_i+1). (This is
natural.)

省去一段阅读体验非常不好且PPT没有涉及的东西

Relations

Binary relation

重中之重：自反性对称性传递性

证明

不可能相等也是antisymmetric

transitive：任意有相邻共同点的两边都能互相到达

Composite of relation

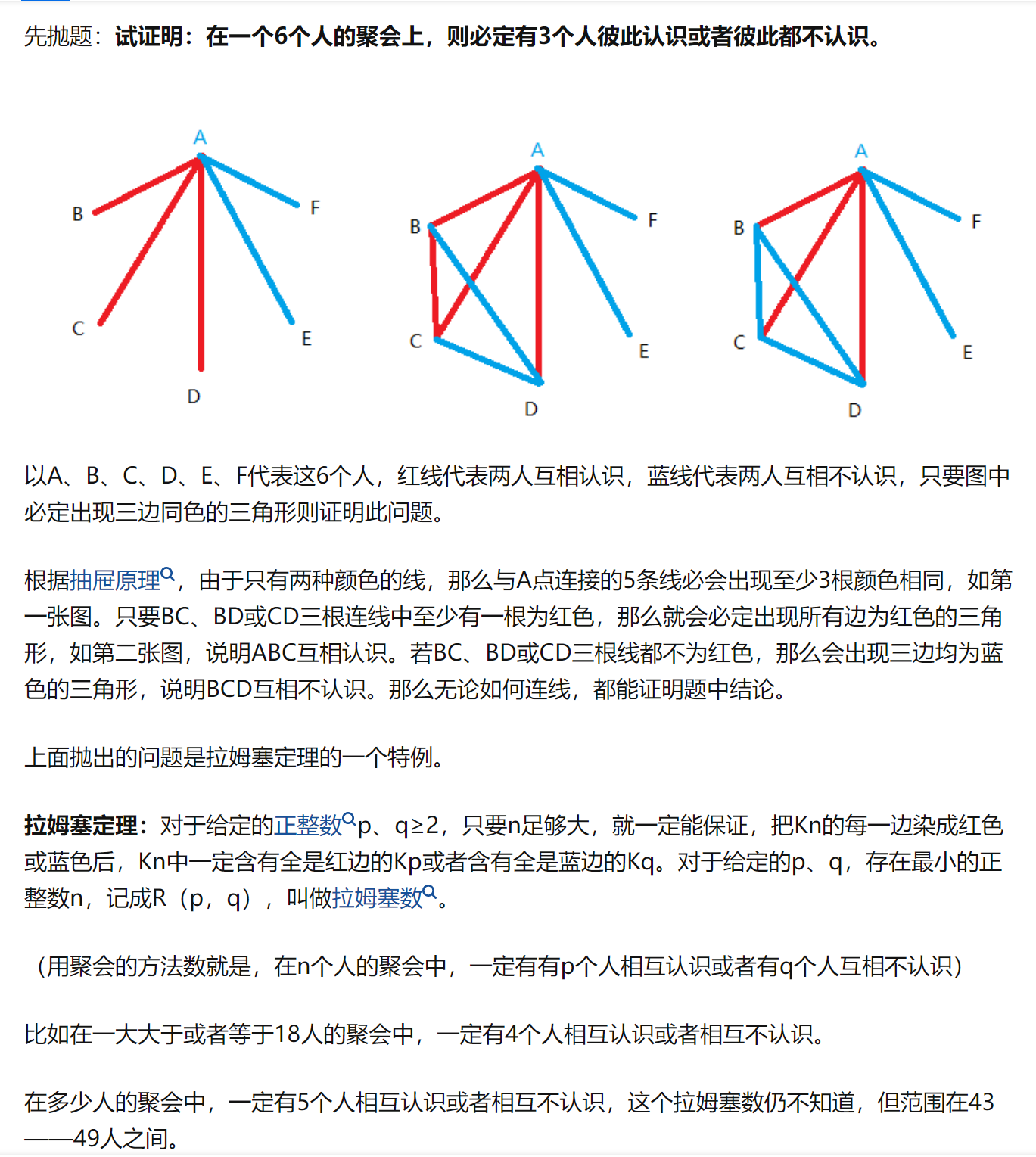
Power of Relation

要注意乘的次序，高次在前面

Transitive

关系矩阵

只要矩阵是对称的，就是symmetric

矩阵乘法+不进位加法：

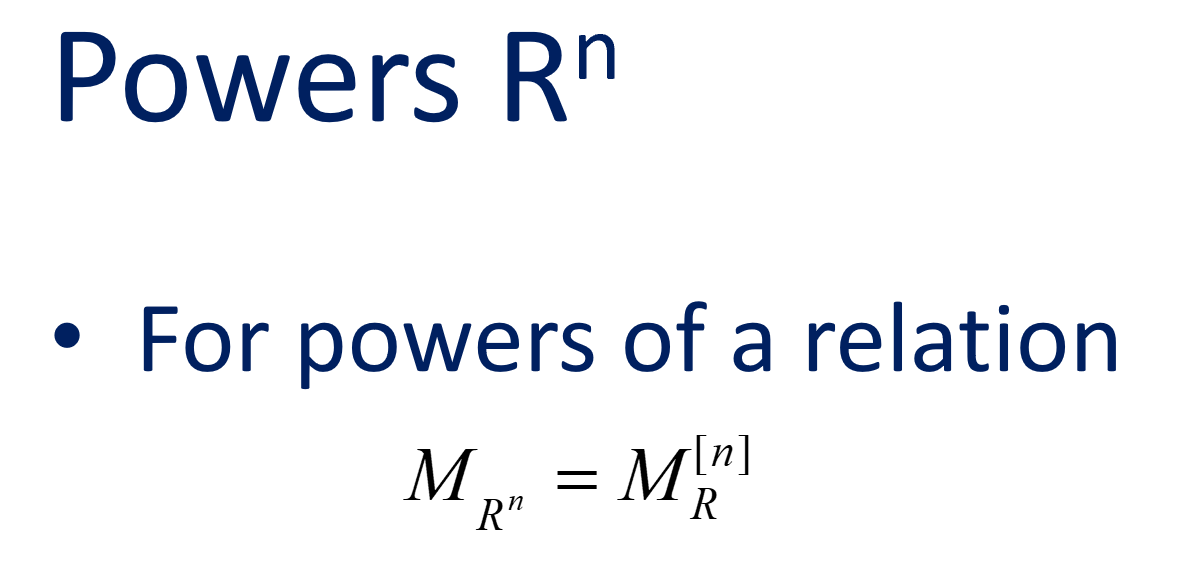
复合

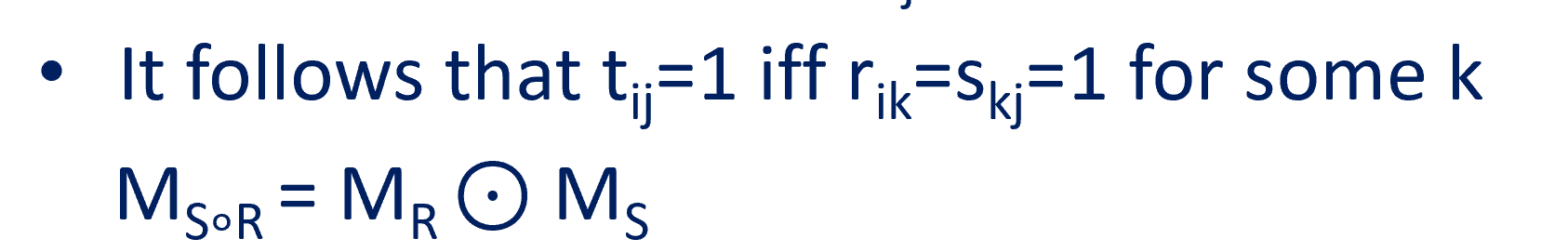
注意顺序反过来

Closures of Relations

（满足关系的最小集？）

自环，反向边，直接边

连通：

易错：

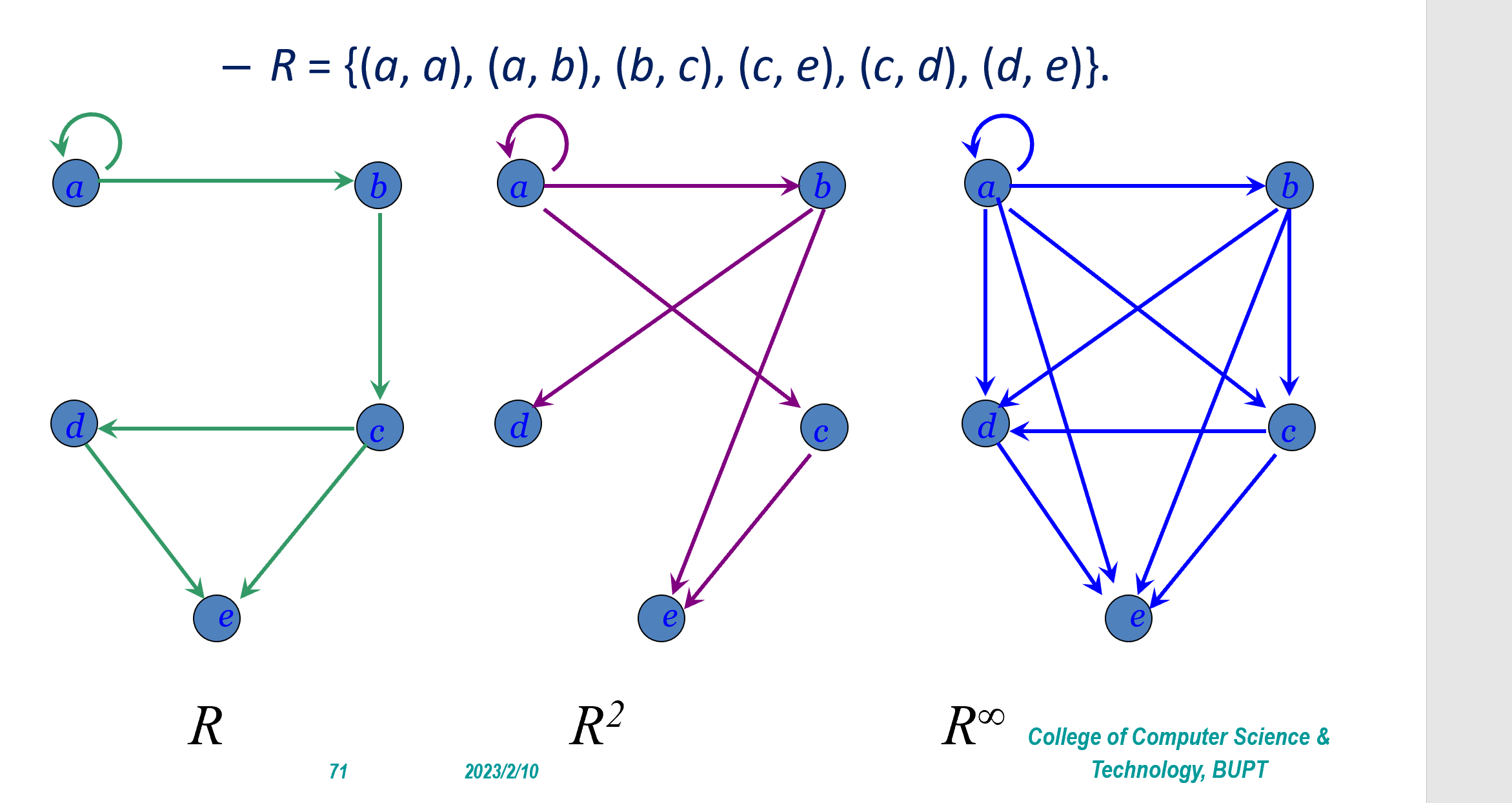
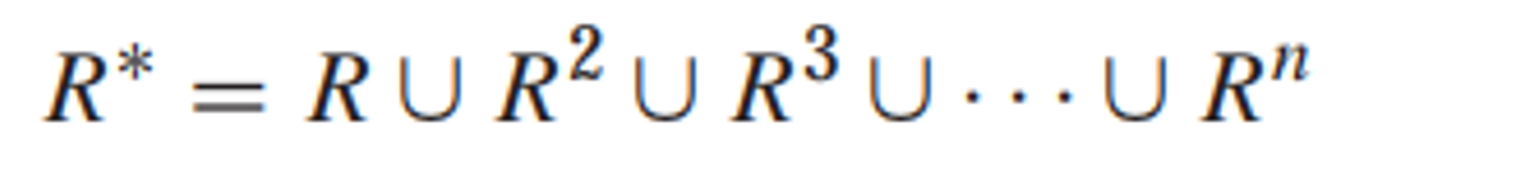
Warshall algorithm

Equivalence

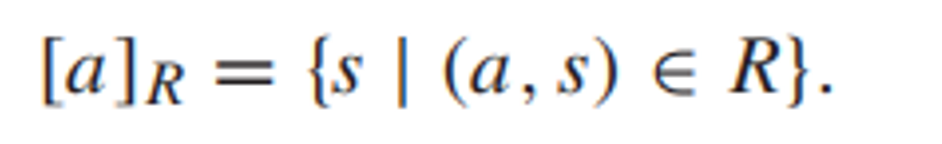
关系R的定义域：domR；值域：ranR；域：fldR=domR∪ranR

偏序关系

偏序关系、全序关系都是公理集合论中的一种二元关系。
偏序集合：配备了偏序关系的集合。
全序集合：配备了全序关系的集合。

偏序：集合内只有部分元素之间在这个关系下是可以比较的。
比如：比如复数集中并不是所有的数都可以比较大小，那么“大小”就是复数集的一个偏序关系。

全序：集合内任何一对元素在在这个关系下都是相互可比较的。
比如：有限长度的序列按字典序是全序的。最常见的是单词在字典中是全序的。

偏序的定义：
设R是集合A上的一个二元关系，若R满足：
Ⅰ 自反性：对任意x∈A，有xRx；
Ⅱ 反对称性（即反对称关系）：对任意x,y∈A，若xRy，且yRx，则x=y；
Ⅲ 传递性：对任意x, y,z∈A，若xRy，且yRz，则xRz。
则称R为A上的偏序关系。

全序的定义：
设集合X上有一全序关系，如果我们把这种关系用 ≤ 表述，则下列陈述对于 X 中的所有 a, b 和 c 成立：
如果 a ≤ b 且 b ≤ a 则 a = b (反对称性)
如果 a ≤ b 且 b ≤ c 则 a ≤ c (传递性)
a ≤ b 或 b ≤ a (完全性)

注意：完全性本身也包括了自反性。
所以，全序关系必是偏序关系。

设(A, ≤)是一偏序集合，B是A的子集。

最大元素、最小元素：
(1)元素b∈B是B的最大元素，如果对每一元素x∈B，x≤b
(2)元素b∈B是B的最小元素，如果对每一元素x∈B，b≤x
即：对于每一个元素，都能满足这样的偏序关系。
定理：如果B存在最大（最小）元素，那么它是唯一的。
例：如果B = {2, 3}，偏序关系为“整除”，因为2和3互相不能整除，那么B没有最小元素和最大元素。

极大元素、极小元素：
(1)如果b∈B，且B中不存在元素x，使b≠x且b≤x，那么元素b∈B叫做B的极大元素。
(2)如果b∈B，且B中不存在元素x，使b≠x且x≤b，那么元素b∈B叫做B的极小元素。
即：对于极大元素，不存在元素在它偏序关系之上。对于极小元素，不存在元素在它偏序关系之下。

注意：B的最大(小)元素和极大(小)元素都必须是子集B的元素，而B的上界(下界)和最小上界(最大下界)可以是也可以不是B的元素。在定义中并没有保证这些元素的存在。在许多情况下他们是不存在的。

上界、下界：
(1)如果对每一b∈B，b≤a，那么元素a∈A叫做B的上界；
(2)如果对于如果对每一b∈B，a≤b，那么元素a∈A叫做B的上界；
上界、下界是A集合里的，可以存在很多个，也可以不存在
也就是说求上界的时候，对于每一个B里面的元素，都要和它上界们满足偏序关系，所以在集合B里面的不能有两个及以上，因为同事选择两个的话，就不满足B里面任何元素都要满足偏序关系了。

上确界、下确界：
(1)如果a是一上界并且对每一B的上界a’有a≤a’，那么元素a∈A叫做B的最小上界，记作lub；
(2)如果a是一下界并且对每一B的下界a’有a≤a’，那么元素a∈A叫做B的最大下界，记作glb
最大下界和最小上界可能存在也可能不存在，如果它们存在，则是唯一的。

如果最大值/最小值/上确界/下确界存在，那么一定是唯一的
求极大值/极小值的时候，因为只要是所有元素没有不满足的就可以，所以可以选择两个以上，其中可以有不和元素连线的。。
求上界/下界，因为是和最大最小值一样是所有的必须满足条件，所以所有元素都是要求有连线的，所以不可能存在两个及以上的元素在B集合里面。。

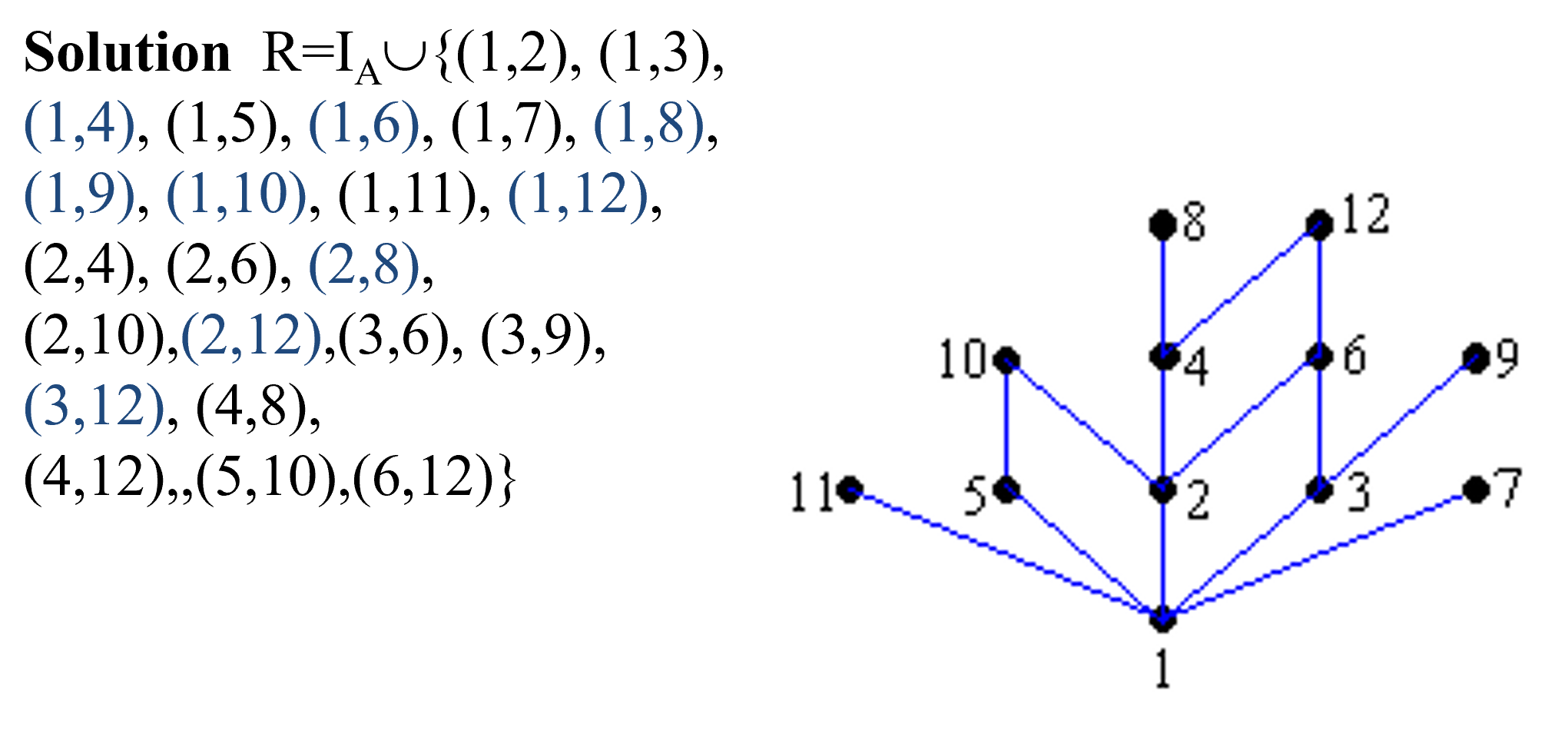
哈斯图画法

先：

然后，相邻两层有直接边的才连在一起。

例子：

极大极小

哈斯图中极大值就是最上层的那几个点，极小值就是最下层的那几个点

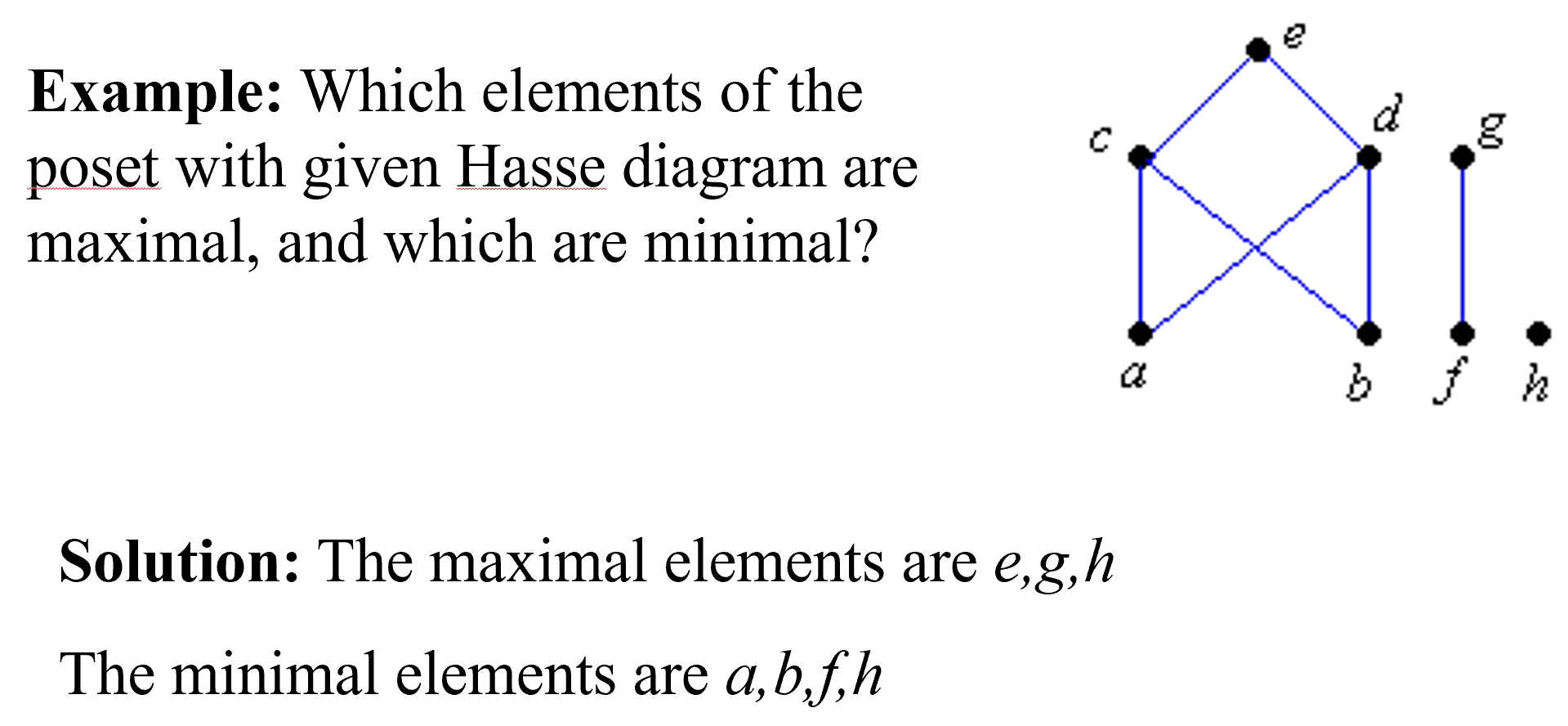
极大元素就是在子集中它的上面没有元素。

极小元素就是在子集中它的下面没有元素。

最大最小

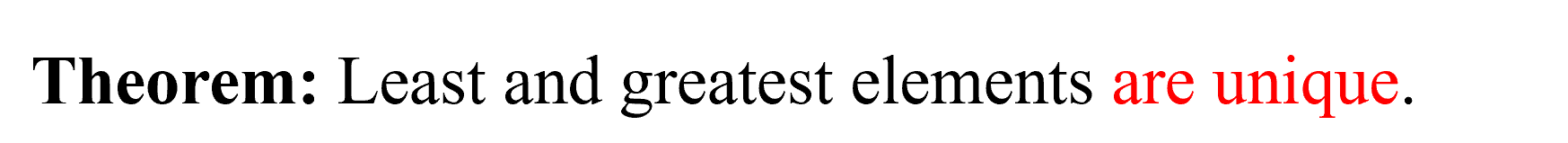
最大元素就是在子集（例题中指B={2，3，5}）中处于最高层且每个元素通过图中路径都可以找到它且它的上面没有元素。

最小元素就是在子集中处于最低层且每个元素通过图中路径都可以找到它且它的下面没有元素。

（记住：这里如果是子集，应当将子集当成一个单独的整体，而不受全集的影响。）

上界下界

上届：所有子集内的元素沿着路径向上都可以找到的元素（这里包括子集和子集以外的元素）。根据上面所说的话，我们可以断定上届也可以是子集内的元素。

下届：所有子集内的元素沿着路径向下都可以找到的元素（这里包括子集和子集以外的元素）。根据上面所说的话，我们可以断定下届也可以是子集内的元素。

上确界：这里我们可以将上届元素看成一个独立的整体，而上确界就是这个集合的最小元，我们称为最小上届。根据上面所说的话，我们可以断定上届也可以是上确界。

下确界：这里我们可以将下届元素看成一个独立的整体，而下确界就是这个集合的最大元，我们称为最大下届。根据上面所说的话，我们可以断定下届也可以是下确界。

我们还拿上面的例子为例：先将子集看为一个整体，再找极大元，极小元，最大元，最小元。

我们发现：2，3，5上面和下面都没有元素，所以2，3，5是极大元，极小元。但是我们发现2，3，5之间压根没线，所以就没有最大元和最小元之说。2，3，5沿向上路径找不到一个元素，所以也没有上确界和上届。2，3，5向下找可以找到一个元素1，所以元素1为下界。下届元素也可以为下确界，自回路嘛，1自己找到自己，所以1也为下确界。

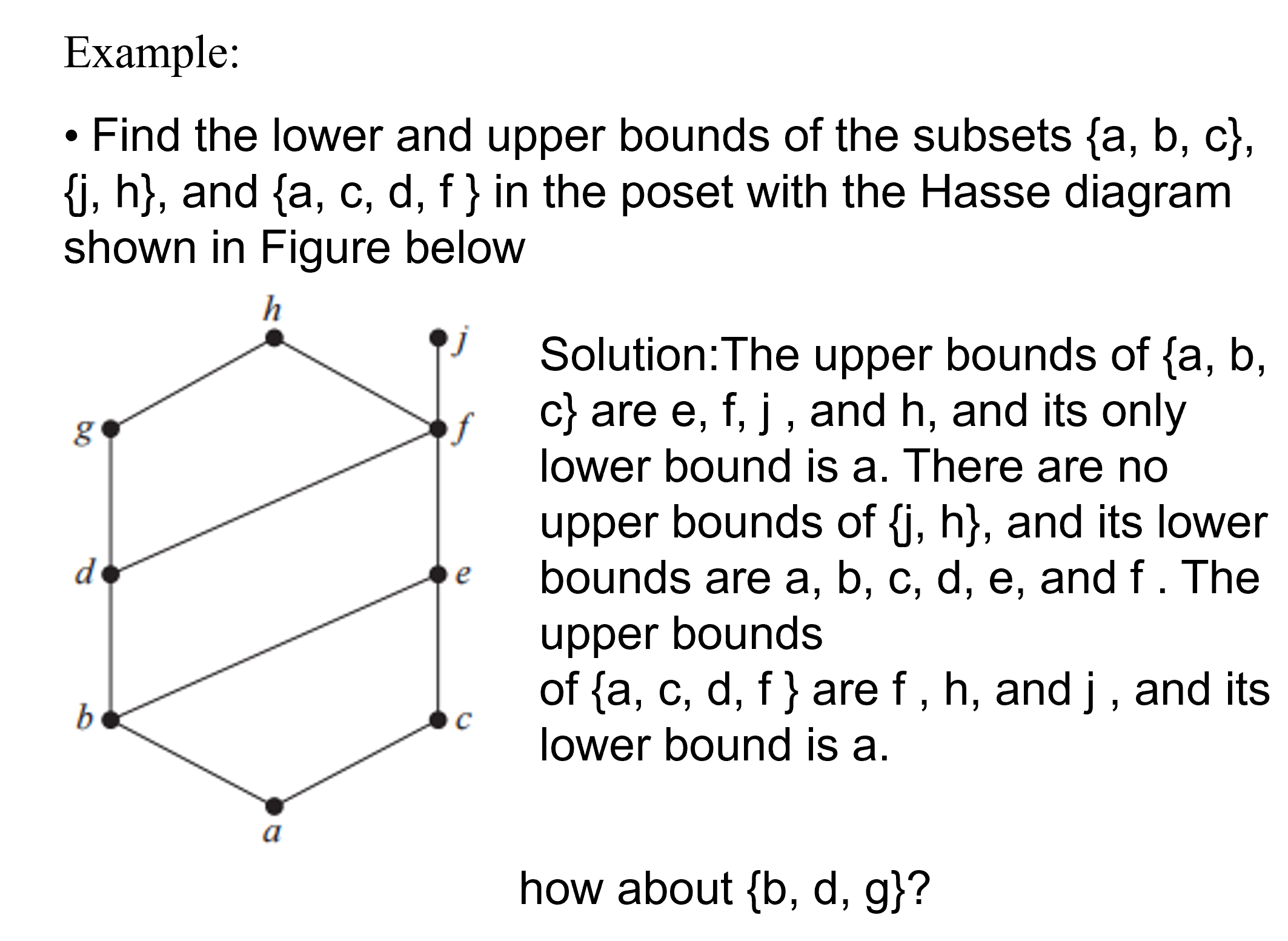
Lattices

例子：不唯一所以不行

Graph

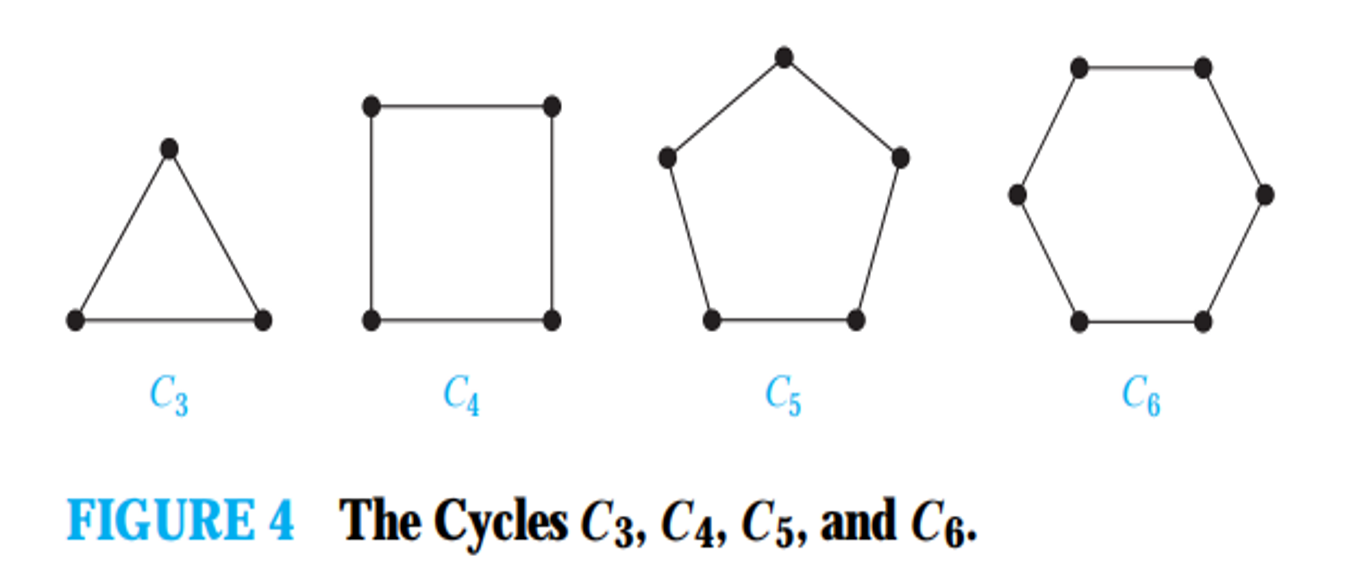
一些特别的图：
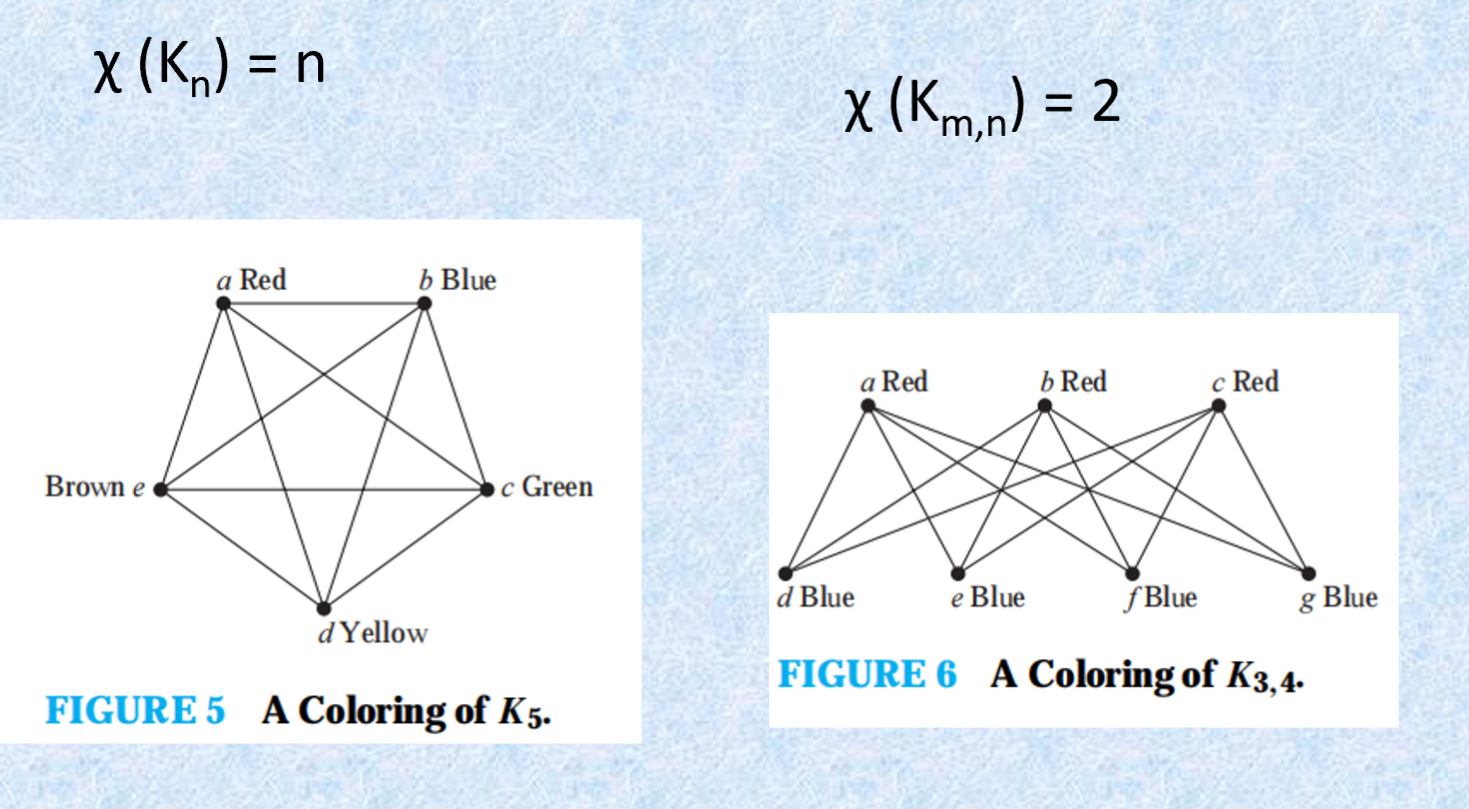
complete graph

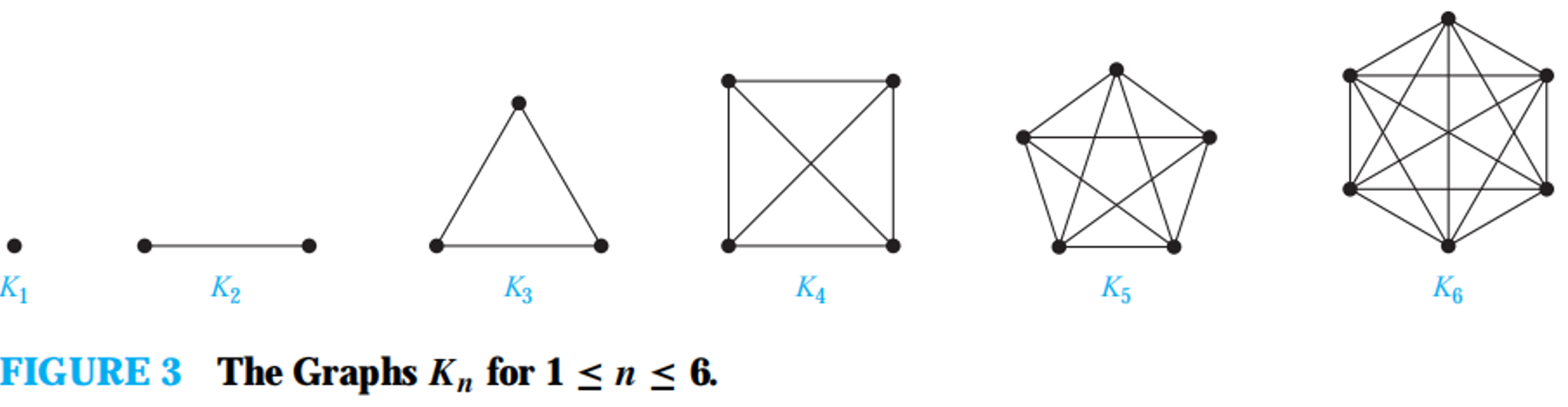
染色法判二分图。如果发现了奇环，那么就不是二分图，否则是。

完全二分图：

oiwiki的二分图部分

假设图有 \(n\) 个顶点，\(m\) 条边。

题目描述

给定一个二分图 \(G\)，即分左右两部分，各部分之间的点没有边连接，要求选出一些边，使得这些边没有公共顶点，且边的数量最大。

增广路算法 Augmenting Path Algorithm

因为增广路长度为奇数，路径起始点非左即右，所以我们先考虑从左边的未匹配点找增广路。
注意到因为交错路的关系，增广路上的第奇数条边都是非匹配边，第偶数条边都是匹配边，于是左到右都是非匹配边，右到左都是匹配边。
于是我们给二分图 定向，问题转换成，有向图中从给定起点找一条简单路径走到某个未匹配点，此问题等价给定起始点 \(s\) 能否走到终点 \(t\)。
那么只要从起始点开始 DFS 遍历直到找到某个未匹配点，\(O(m)\)。
未找到增广路时，我们拓展的路也称为 交错树。

性质

因为要枚举 \(n\) 个点，总复杂度为 \(O(nm)\)。

实现

struct augment_path {
  vector<vector<int> > g;
  vector<int> pa;  // 匹配
  vector<int> pb;
  vector<int> vis;  // 访问
  int n, m;         // 两个点集中的顶点数量
  int dfn;          // 时间戳记
  int res;          // 匹配数

  augment_path(int _n, int _m) : n(_n), m(_m) {
    assert(0 <= n && 0 <= m);
    pa = vector<int>(n, -1);
    pb = vector<int>(m, -1);
    vis = vector<int>(n);
    g.resize(n);
    res = 0;
    dfn = 0;
  }

  void add(int from, int to) {
    assert(0 <= from && from < n && 0 <= to && to < m);
    g[from].push_back(to);
  }

  bool dfs(int v) {
    vis[v] = dfn;
    for (int u : g[v]) {
      if (pb[u] == -1) {
        pb[u] = v;
        pa[v] = u;
        return true;
      }
    }
    for (int u : g[v]) {
      if (vis[pb[u]] != dfn && dfs(pb[u])) {
        pa[v] = u;
        pb[u] = v;
        return true;
      }
    }
    return false;
  }

  int solve() {
    while (true) {
      dfn++;
      int cnt = 0;
      for (int i = 0; i < n; i++) {
        if (pa[i] == -1 && dfs(i)) {
          cnt++;
        }
      }
      if (cnt == 0) {
        break;
      }
      res += cnt;
    }
    return res;
  }
};

补充

二分图最小点覆盖（König 定理）

最小点覆盖：选最少的点，满足每条边至少有一个端点被选。

二分图中，最小点覆盖 \(=\) 最大匹配。

"证明"
将二分图点集分成左右两个集合，使得所有边的两个端点都不在一个集合。

考虑如下构造：从左侧未匹配的节点出发，按照匈牙利算法中增广路的方式走，即先走一条未匹配边，再走一条匹配边。由于已经求出了最大匹配，所以这样的增广路一定以匹配边结束。在所有经过这样“增广路”的节点上打标记。则最后构造的集合是：所有左侧未打标记的节点和所有右侧打了标记的节点。

首先，易证这个集合的大小等于最大匹配。打了标记的节点一定都是匹配边上的点，一条匹配的边两侧一定都有标记（在增广路上）或都没有标记，所以两个节点中必然有一个被选中。

其次，这个集合是一个点覆盖。一条匹配边一定有一个点被选中，而一条未匹配的边一定是增广路的一部分，而右侧端点也一定被选中。

同时，不存在更小的点覆盖。为了覆盖最大匹配的所有边，至少要有最大匹配边数的点数。

二分图最大独立集

最大独立集：选最多的点，满足两两之间没有边相连。

因为在最小点覆盖中，任意一条边都被至少选了一个顶点，所以对于其点集的补集，任意一条边都被至多选了一个顶点，所以不存在边连接两个点集中的点，且该点集最大。因此二分图中，最大独立集 \(=n-\) 最小点覆盖。

二分图的最大权匹配是指二分图中边权和最大的匹配。

Hungarian Algorithm（Kuhn-Munkres Algorithm）

匈牙利算法又称为 KM 算法，可以在 \(O(n^3)\) 时间内求出二分图的 最大权完美匹配。

考虑到二分图中两个集合中的点并不总是相同，为了能应用 KM 算法解决二分图的最大权匹配，需要先作如下处理：将两个集合中点数比较少的补点，使得两边点数相同，再将不存在的边权重设为 \(0\)，这种情况下，问题就转换成求 最大权完美匹配问题，从而能应用 KM 算法求解。

"可行顶标"
给每个节点 \(i\) 分配一个权值 \(l(i)\)，对于所有边 \((u,v)\) 满足 \(w(u,v) \leq l(u) + l(v)\)。

"相等子图"
在一组可行顶标下原图的生成子图，包含所有点但只包含满足 \(w(u,v) = l(u) + l(v)\) 的边 \((u,v)\)。

"定理 1 : 对于某组可行顶标，如果其相等子图存在完美匹配，那么，该匹配就是原二分图的最大权完美匹配。"
证明 1.

考虑原二分图任意一组完美匹配 $M$，其边权和为

$val(M) = \sum_{(u,v)\in M} {w(u,v)} \leq \sum_{(u,v)\in M} {l(u) + l(v)} \leq \sum_{i=1}^{n} l(i)$

任意一组可行顶标的相等子图的完美匹配 $M'$ 的边权和

$val(M') = \sum_{(u,v)\in M} {l(u) + l(v)} = \sum_{i=1}^{n} l(i)$

即任意一组完美匹配的边权和都不会大于 $val(M')$，那个 $M'$ 就是最大权匹配。

有了定理 1，我们的目标就是透过不断的调整可行顶标，使得相等子图是完美匹配。

因为两边点数相等，假设点数为 \(n\)，\(lx(i)\) 表示左边第 \(i\) 个点的顶标，\(ly(i)\) 表示右边第 \(i\) 个点的顶标，\(w(u,v)\) 表示左边第 \(u\) 个点和右边第 \(v\) 个点之间的权重。

首先初始化一组可行顶标，例如

\(lx(i) = \max_{1\leq j\leq n} \{ w(i, j)\},\, ly(i) = 0\)

然后选一个未匹配点，如同最大匹配一样求增广路。找到增广路就增广，否则，会得到一个交错树。

令 \(S\)，\(T\) 表示二分图左边右边在交错树中的点，\(S'\)，\(T'\) 表示不在交错树中的点。

在相等子图中：

• \(S-T'\) 的边不存在，否则交错树会增长。
• \(S'-T\) 一定是非匹配边，否则他就属于 \(S\)。

假设给 \(S\) 中的顶标 \(-a\)，给 \(T\) 中的顶标 \(+a\)，可以发现

• \(S-T\) 边依然存在相等子图中。
• \(S'-T'\) 没变化。
• \(S-T'\) 中的 \(lx + ly\) 有所减少，可能加入相等子图。
• \(S'-T\) 中的 \(lx + ly\) 会增加，所以不可能加入相等子图。

所以这个 \(a\) 值的选择，显然得是 \(S-T'\) 当中最小的边权，

\(a = \min \{ lx(u) + ly(v) - w(u,v) | u\in{S} , v\in{T'} \}\)。

当一条新的边 \((u,v)\) 加入相等子图后有两种情况

• \(v\) 是未匹配点，则找到增广路
• \(v\) 和 \(S'\) 中的点已经匹配

这样至多修改 \(n\) 次顶标后，就可以找到增广路。

每次修改顶标的时候，交错树中的边不会离开相等子图，那么我们直接维护这棵树。

我们对 \(T\) 中的每个点 \(v\) 维护

\(slack(v) = \min \{ lx(u) + ly(v) - w(u,v) | u\in{S} \}\)。

所以可以在 \(O(n)\) 算出顶标修改值 \(a\)

\(a = \min \{ slack(v) | v\in{T'} \}\)

交错树新增一个点进入 \(S\) 的时候需要 \(O(n)\) 更新 \(slack(v)\)。修改顶标需要 \(O(n)\) 给每个 \(slack(v)\) 减去 \(a\)。只要交错树找到一个未匹配点，就找到增广路。

一开始枚举 \(n\) 个点找增广路，为了找增广路需要延伸 \(n\) 次交错树，每次延伸需要 \(n\) 次维护，共 \(O(n^3)\)。

??? note "参考代码"
```cpp
template
struct hungarian { // km
int n;
vector matchx; // 左集合对应的匹配点
vector matchy; // 右集合对应的匹配点
vector pre; // 连接右集合的左点
vector visx; // 拜访数组 左
vector visy; // 拜访数组 右
vector lx;
vector ly;
vector<vector > g;
vector slack;
T inf;
T res;
queue q;
int org_n;
int org_m;

  hungarian(int _n, int _m) {
    org_n = _n;
    org_m = _m;
    n = max(_n, _m);
    inf = numeric_limits<T>::max();
    res = 0;
    g = vector<vector<T> >(n, vector<T>(n));
    matchx = vector<int>(n, -1);
    matchy = vector<int>(n, -1);
    pre = vector<int>(n);
    visx = vector<bool>(n);
    visy = vector<bool>(n);
    lx = vector<T>(n, -inf);
    ly = vector<T>(n);
    slack = vector<T>(n);
  }

  void addEdge(int u, int v, int w) {
    g[u][v] = max(w, 0);  // 负值还不如不匹配 因此设为0不影响
  }

  bool check(int v) {
    visy[v] = true;
    if (matchy[v] != -1) {
      q.push(matchy[v]);
      visx[matchy[v]] = true;  // in S
      return false;
    }
    // 找到新的未匹配点 更新匹配点 pre 数组记录着"非匹配边"上与之相连的点
    while (v != -1) {
      matchy[v] = pre[v];
      swap(v, matchx[pre[v]]);
    }
    return true;
  }

  void bfs(int i) {
    while (!q.empty()) {
      q.pop();
    }
    q.push(i);
    visx[i] = true;
    while (true) {
      while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int v = 0; v < n; v++) {
          if (!visy[v]) {
            T delta = lx[u] + ly[v] - g[u][v];
            if (slack[v] >= delta) {
              pre[v] = u;
              if (delta) {
                slack[v] = delta;
              } else if (check(v)) {  // delta=0 代表有机会加入相等子图 找增广路
                                      // 找到就return 重建交错树
                return;
              }
            }
          }
        }
      }
      // 没有增广路 修改顶标
      T a = inf;
      for (int j = 0; j < n; j++) {
        if (!visy[j]) {
          a = min(a, slack[j]);
        }
      }
      for (int j = 0; j < n; j++) {
        if (visx[j]) {  // S
          lx[j] -= a;
        }
        if (visy[j]) {  // T
          ly[j] += a;
        } else {  // T'
          slack[j] -= a;
        }
      }
      for (int j = 0; j < n; j++) {
        if (!visy[j] && slack[j] == 0 && check(j)) {
          return;
        }
      }
    }
  }

  void solve() {
    // 初始顶标
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < n; j++) {
        lx[i] = max(lx[i], g[i][j]);
      }
    }

    for (int i = 0; i < n; i++) {
      fill(slack.begin(), slack.end(), inf);
      fill(visx.begin(), visx.end(), false);
      fill(visy.begin(), visy.end(), false);
      bfs(i);
    }

    // custom
    for (int i = 0; i < n; i++) {
      if (g[i][matchx[i]] > 0) {
        res += g[i][matchx[i]];
      } else {
        matchx[i] = -1;
      }
    }
    cout << res << "\n";
    for (int i = 0; i < org_n; i++) {
      cout << matchx[i] + 1 << " ";
    }
    cout << "\n";
  }
};
```

Dynamic Hungarian Algorithm

原论文 The Dynamic Hungarian Algorithm for the Assignment Problem with Changing Costs

伪代码更清晰的论文 A Fast Dynamic Assignment Algorithm for Solving Resource Allocation Problems

相关 OJ 问题 DAP

???+ note "算法思路"
1. 修改单点 \(u_i\) 和所有 \(v_j\) 之间的权重，即权重矩阵中的一行
- 修改顶标 \(lx(u_i) = max(w_{ij} - v_{j}), \forall j\)
- 删除 \(u_i\) 相关的匹配
2. 修改所有 \(u_i\) 和单点 \(v_j\) 之间的权重，即权重矩阵中的一列
- 修改顶标 \(ly(v_j) = max(w_{ij} - u_{i}), \forall i\)
- 删除 \(v_j\) 相关的匹配
3. 修改单点 \(u_i\) 和单点 \(v_j\) 之间的权重，即权重矩阵中的单个元素
- 做 1 或 2 两种操作之一即可
4. 添加某一单点 \(u_i\)，或者某一单点 \(v_j\)，即在权重矩阵中添加或者删除一行或者一列
- 对应地做 1 或 2 即可，注意此处加点操作仅为加点，不额外设定权重值，新加点与其他点的权重为 0.

???+ note "算法证明"
- 设原图为 G，左右两边的顶标为 \(\alpha^{i}\) 和 \(\beta^{j}\)，可行顶标为 l，那 \(G_l\) 是 G 的一个子图，包含图 G 中满足 \(w_{ij} = alpha_{i}+beta_{j}\) 的点和边。
- 在上面匈牙利算法的部分，定理一证明了：对于某组可行顶标，如果其相等子图存在完美匹配，那么，该匹配就是原二分图的最大权完美匹配。
- 假设原来的最优匹配是 \(M^*\), 当一个修改发生的时候，我们会根据规则更新可行顶标，更新后的顶标设为 \(\alpha^{i^*}\), 或者 \(\beta^{j^*}\)，会出现以下情况：
1. 权重矩阵的一整行被修改了，设被修改的行为 \(i^*\) 行，即 \(v_{i^*}\) 的所有边被修改了，所以 \(v_{i^*}\) 原来的顶标可能不满足条件，因为我们需要 \(w_{i^{*}j} \leq alpha_{i^*}+beta_{j}\)，但对于其他的 \(u_j\) 来说，除了 \(i^*\) 相关的边，他们的边权是不变的，因此他们的顶标都是合法的，所以算法中修改了 \(v_{i^*}\) 相关的顶标使得这组顶标是一组可行顶标。
2. 权重矩阵的一整列被修改了，同理可得算法修改顶标使得这组顶标是一组可行顶标。
3. 修改权重矩阵某一元素，任意修改其中一个顶标即可满足顶标条件
- 每一次权重矩阵被修改，都关系到一个特定节点，这个节点可能是左边的也可能是右边的，因此我们直接记为 \(x\), 这个节点和某个节点 \(y\) 在原来的最优匹配中匹配上了。每一次修改操作，最多让这一对节点 unpair，因此我们只要跑一轮匈牙利算法中的搜索我们就能得到一个新的 match，而根据定理一，新跑出来的 match 是最优的。

以下代码应该为论文 2 作者提交的代码（以下代码为最大化权重版本，原始论文中为最小化 cost）

??? note "动态匈牙利算法参考代码"
cpp --8<-- "docs/graph/graph-matching/code/bigraph-weight-match/bigraph-weight-match_1.cpp"

转化为费用流模型

在图中新增一个源点和一个汇点。

从源点向二分图的每个左部点连一条流量为 \(1\)，费用为 \(0\) 的边，从二分图的每个右部点向汇点连一条流量为 \(1\)，费用为 \(0\) 的边。

接下来对于二分图中每一条连接左部点 \(u\) 和右部点 \(v\)，边权为 \(w\) 的边，则连一条从 \(u\) 到 \(v\)，流量为 \(1\)，费用为 \(w\) 的边。

求这个网络的 最大费用最大流 即可得到答案。

习题

??? note "UOJ #80. 二分图最大权匹配 "
模板题

```cpp
--8<-- "docs/graph/graph-matching/code/bigraph-weight-match/bigraph-weight-match_2.cpp"
```

同构

同构：邻接矩阵相等。

不同构：存在某种性质不共有

强连通：有向图 G 强连通是指，G 中任意两个结点连通。
弱联通 weakly connected：把边视为无向之后是连通的
单向连通 unilaterally connected：任意两点之间单向可达。

欧拉图

• 欧拉回路：通过图中每条边恰好一次的回路
• 欧拉通路：通过图中每条边恰好一次的通路
• 欧拉图：具有欧拉回路的图
• 半欧拉图：具有欧拉通路但不具有欧拉回路的图

欧拉图中所有顶点的度数都是偶数。

若 \(G\) 是欧拉图，则它为若干个环的并，且每条边被包含在奇数个环内。

判别法

1. 无向图是欧拉图当且仅当：
   • 非零度顶点是连通的
   • 顶点的度数都是偶数
2. 无向图是半欧拉图当且仅当：
   • 非零度顶点是连通的
   • 恰有 0 或 2 个奇度顶点
3. 有向图是欧拉图当且仅当：
   • 非零度顶点是强连通的
   • 每个顶点的入度和出度相等
4. 有向图是半欧拉图当且仅当：
   • 非零度顶点是弱连通的
   • 至多一个顶点的出度与入度之差为 1
   • 至多一个顶点的入度与出度之差为 1
   • 其他顶点的入度和出度相等

哈密顿通路

通过图中所有顶点一次且仅一次的通路称为哈密顿通路。

通过图中所有顶点一次且仅一次的回路称为哈密顿回路。

具有哈密顿回路的图称为哈密顿图。

具有哈密顿通路而不具有哈密顿回路的图称为半哈密顿图。

判定：

性质：

设 \(G=<V, E>\) 是哈密顿图，则对于 \(V\) 的任意非空真子集 \(V_1\)，均有 \(p(G-V_1) \leq |V_1|\)。其中 \(p(x)\) 为 \(x\) 的连通分支数。

推论：设 \(G=<V, E>\) 是半哈密顿图，则对于 \(V\) 的任意非空真子集 \(V_1\)，均有 \(p(G-V_1) \leq |V_1|+1\)。其中 \(p(x)\) 为 \(x\) 的连通分支数。

完全图 \(K_{2k+1} (k \geq 1)\) 中含 \(k\) 条边不重的哈密顿回路，且这 \(k\) 条边不重的哈密顿回路含 \(K_{2k+1}\) 中的所有边。

完全图 \(K_{2k} (k \geq 2)\) 中含 \(k-1\) 条边不重的哈密顿回路，从 \(K_{2k}\) 中删除这 \(k-1\) 条边不重的哈密顿回路后所得图含 \(k\) 条互不相邻的边。

最短路

dijkstra （简单图 + 正权）

int dijkstra () {
    memset (dis, 0x3f, sizeof dis);
    dis[1] = 0;
    for (int i = 1; i <= n; i ++){
        int t = -1;
        for (int j = 1; j <= n; j ++)
            if (!vis[j] && (t == -1 || dis[j] < dis[t]))
                t = j;
        for (int j = 1; j <= n; j ++)
            dis[j] = min (dis[j], dis[t] + a[t][j]);
        vis[t] = true;
    }
    if (dis[n] == 0x3f3f3f3f)
        return -1;
    return dis[n];
        
}

Planar Graphs 平面图

homeomorphic: 同胚性

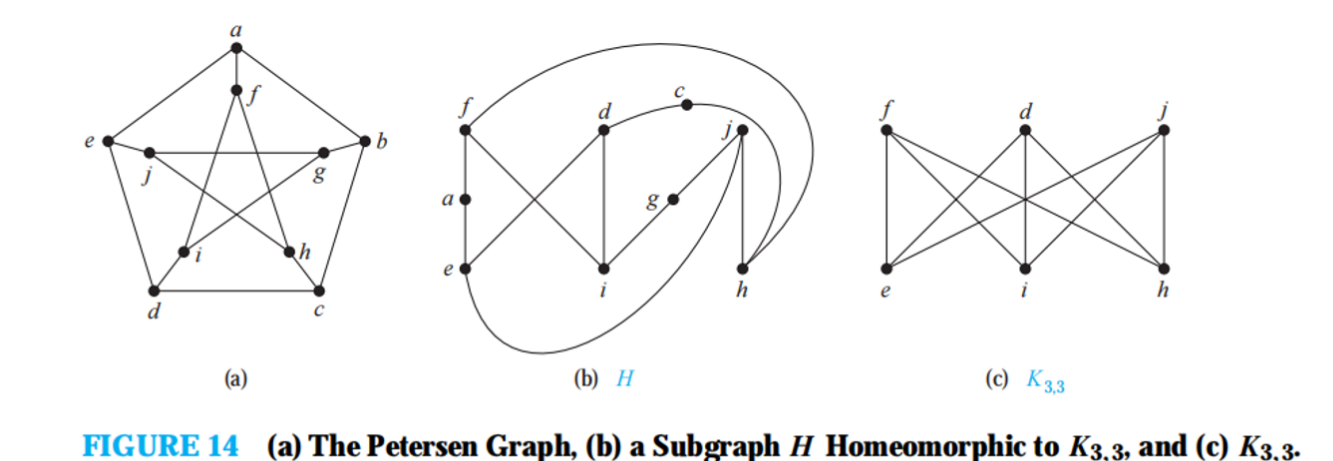
染色

树

A rooted m-ary tree of height h is balanced if all leaves are at levels h or h − 1.
M叉数叶子的数量：There are at most mh leaves in an m-ary tree of height h.

Binary Search Trees

小的放左子，大的放右子

Decision Trees

Binary sorting

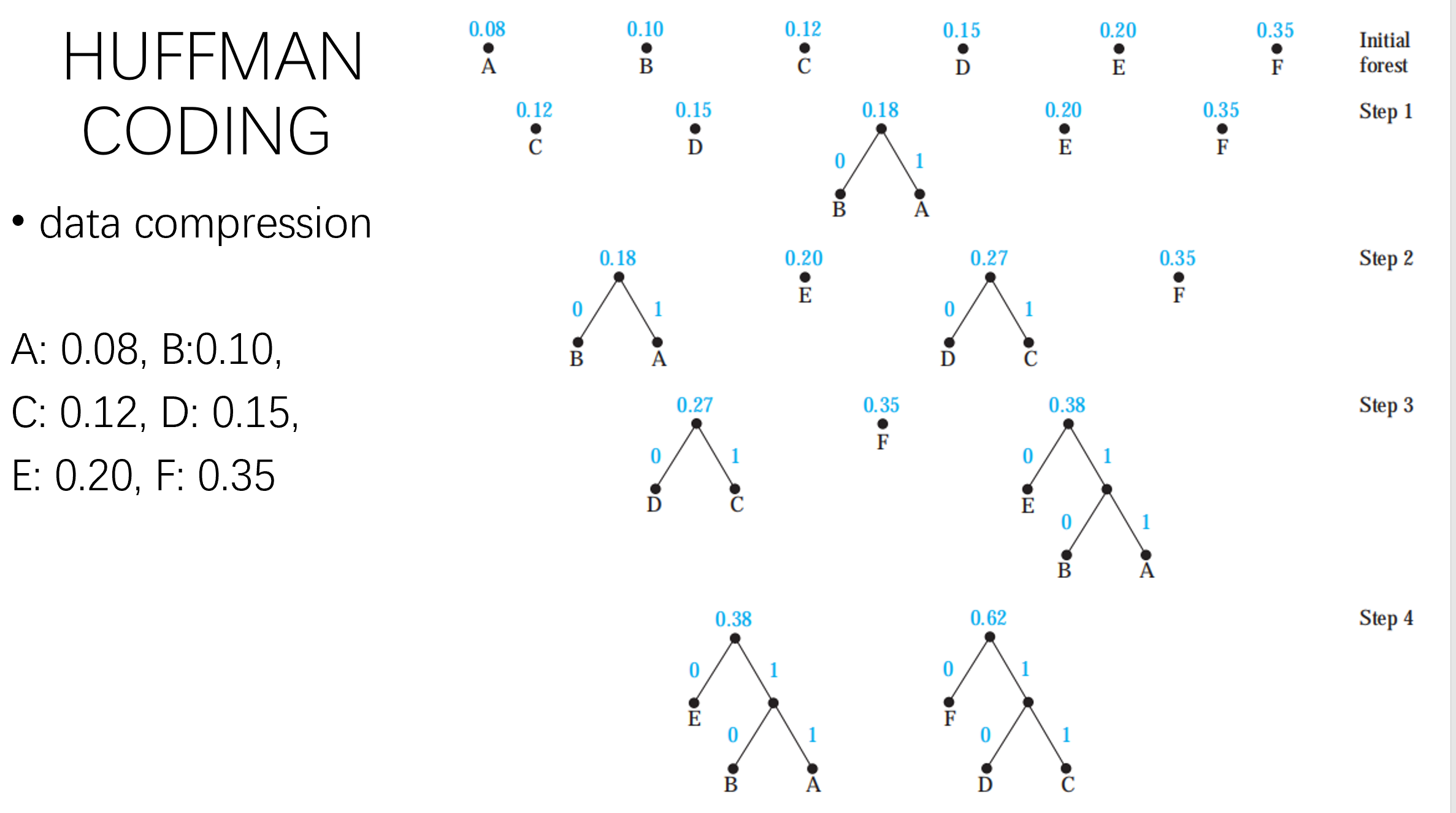
Prefix Code: Huffan

不会互为前缀

Tree Traversal

preorder traversal：根左右
inorder traversal：左根右
postorder traversal：左右根

Spanning Trees

A simple graph is connected if and only if it has a spanning tree.

MST

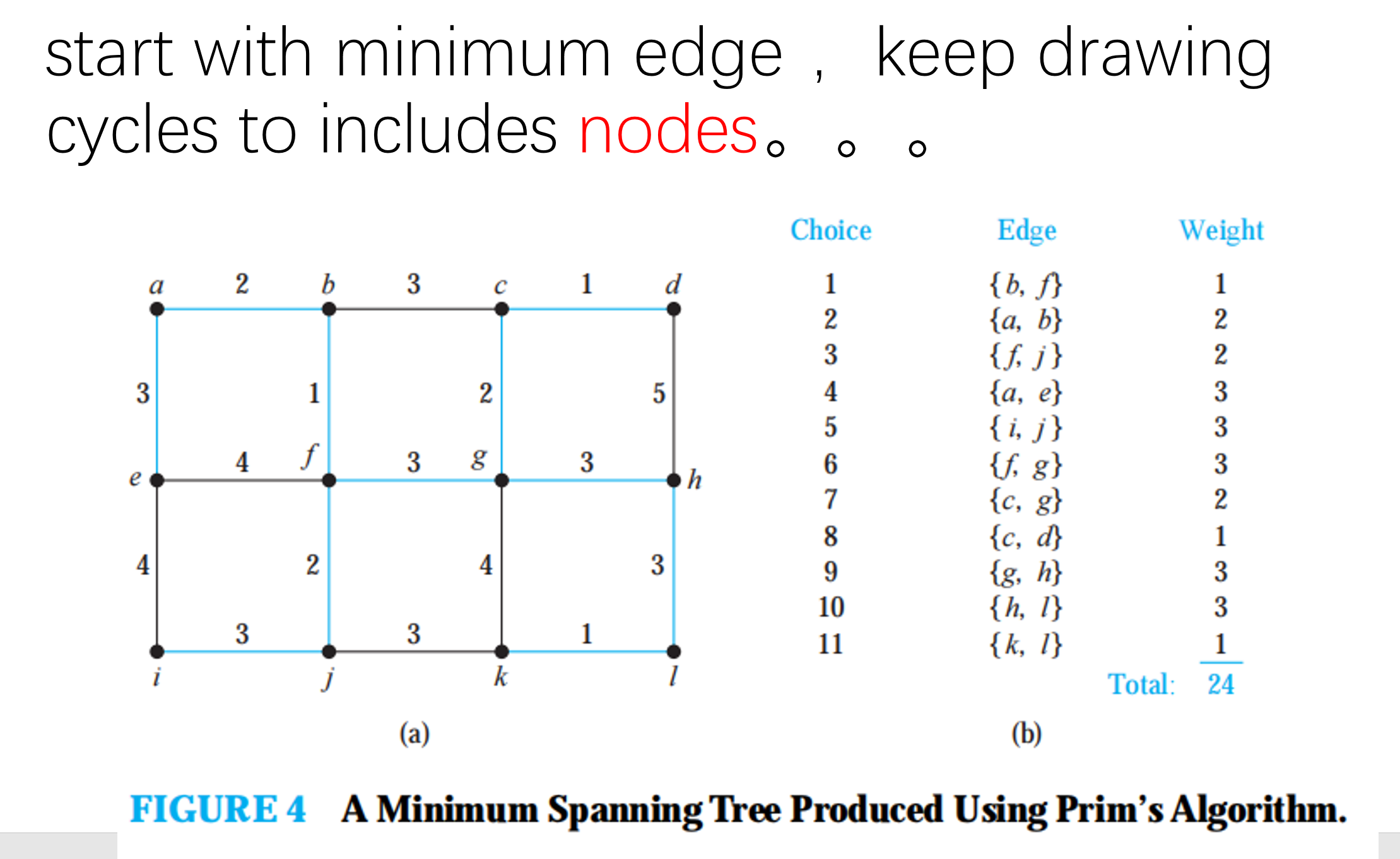
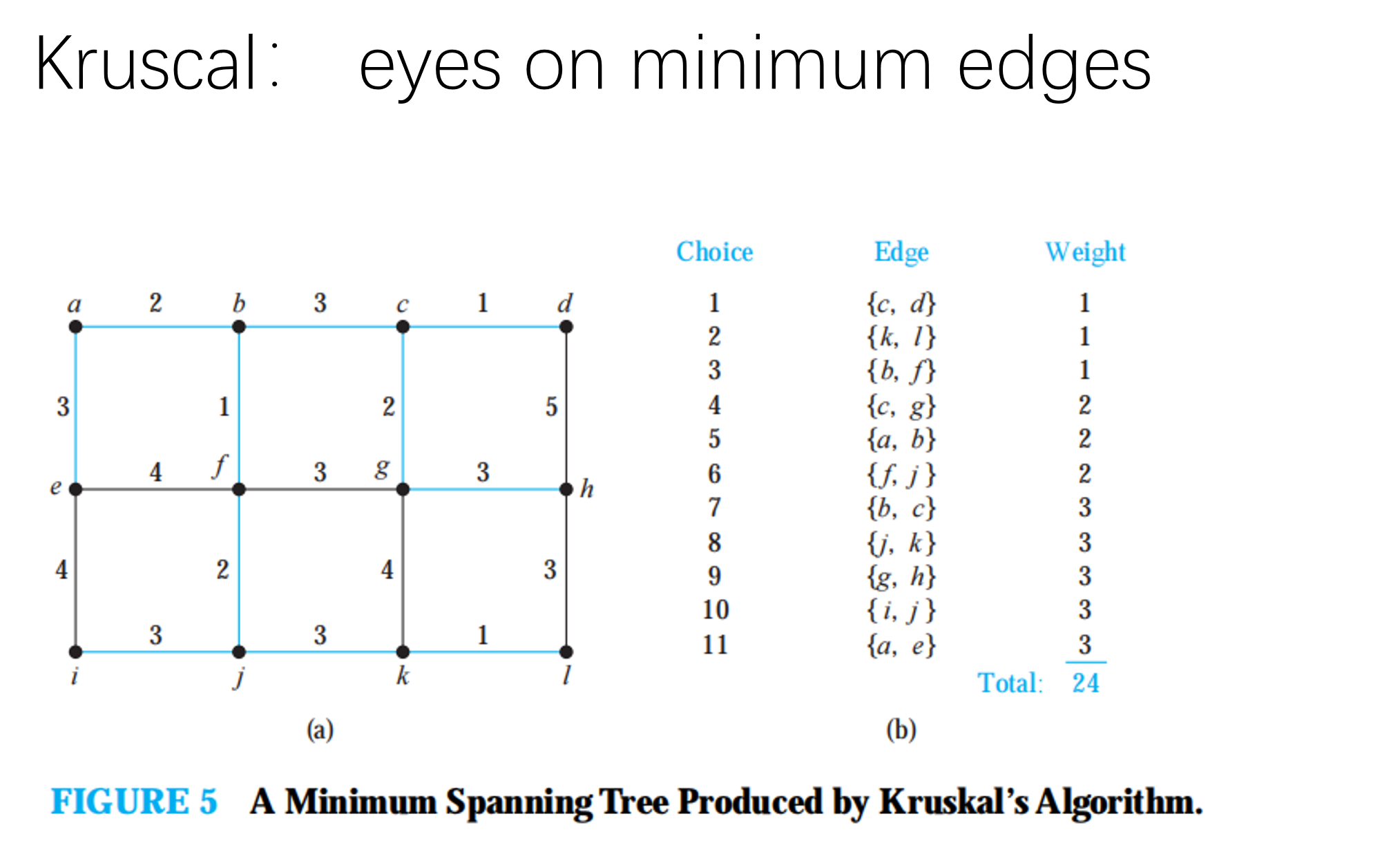
int prim(int s){
    memset (dis, 0x3f, sizeof dis);
    dis[s] = 0;

    int ans = 0;
    for (int i = 0; i < n; i ++){
        int t = -1;
        for (int j = 1; j <= n; j ++){
            if (vis[j])		continue;
            if (t == -1 || dis[t] > dis[j])    t = j;
        }
        if (dis[t] == INF)    return INF;

        ans += dis[t];
        vis[t] = true;

        for (int j = 1; j <= n; j ++)    dis[j] = min (dis[j], a[t][j]);
    }
    return ans;
}

struct Edge{
    int a, b, w;
    bool operator< (const Edge &W)const{
        return w < W.w;
    }
}e[M];

void init(){
    for (int i = 1; i <= n; i ++)
        fa[i] = i;
}

int find(int x){
    if (fa[x] != x)
        fa[x] = find(fa[x]);
    return fa[x];
}

int kruskal(){
    sort (e, e + m);
    init();
    int ans = 0, cnt = 0;

    for (int i = 0; i < m; i ++){
        int a = e[i].a, b = e[i].b, w = e[i].w;
        a = find(a), b = find(b);
        if (a != b){
            fa[a] = b;
            ans += w;
            cnt ++;
        }//不连通就加入集合
    }

    if (cnt < n - 1)
        return INF;
    return ans;
}

oiwiki上的图论概念

本页面概述了图论中的一些概念，这些概念并不全是在 OI 中常见的，对于 OIer 来说，只需掌握本页面中的基础部分即可，如果在学习中碰到了不懂的概念，可以再来查阅。

!!! warning
图论相关定义在不同教材中往往会有所不同，遇到的时候需根据上下文加以判断。

图

图 (graph) 是一个二元组 \(G=(V(G), E(G))\)。其中 \(V(G)\) 是非空集，称为 点集 (vertex set)，对于 \(V\) 中的每个元素，我们称其为 顶点 (vertex) 或 节点 (node)，简称 点；\(E(G)\) 为 \(V(G)\) 各结点之间边的集合，称为 边集 (edge set)。

常用 \(G=(V,E)\) 表示图。

当 \(V,E\) 都是有限集合时，称 \(G\) 为 有限图。

当 \(V\) 或 \(E\) 是无限集合时，称 \(G\) 为 无限图。

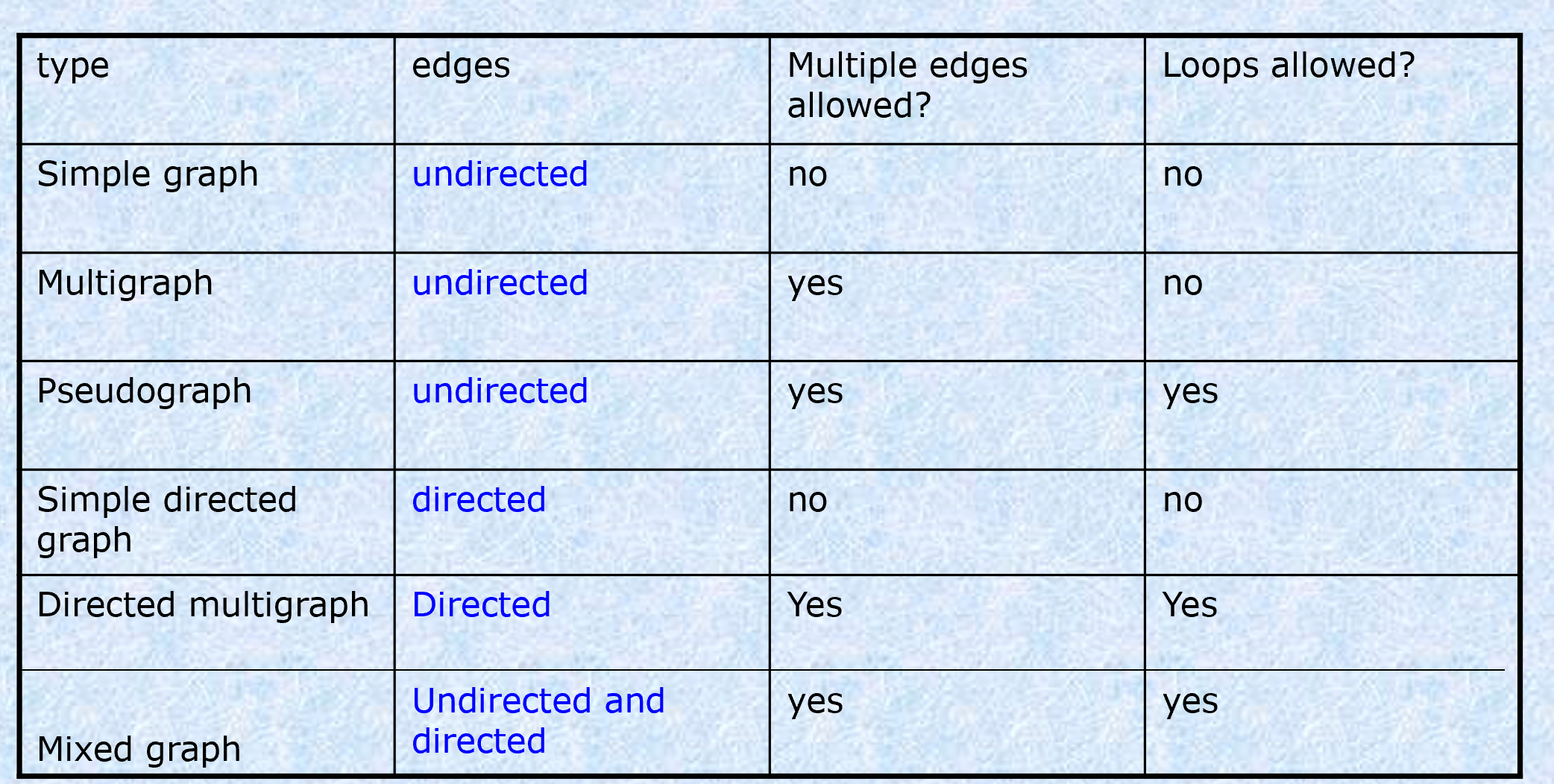
图有多种，包括 无向图 (undirected graph)，有向图 (directed graph)，混合图 (mixed graph) 等。

若 \(G\) 为无向图，则 \(E\) 中的每个元素为一个无序二元组 \((u, v)\)，称作 无向边 (undirected edge)，简称 边 (edge)，其中 \(u, v \in V\)。设 \(e = (u, v)\)，则 \(u\) 和 \(v\) 称为 \(e\) 的 端点 (endpoint)。

若 \(G\) 为有向图，则 \(E\) 中的每一个元素为一个有序二元组 \((u, v)\)，有时也写作 \(u \to v\)，称作 有向边 (directed edge) 或 弧 (arc)，在不引起混淆的情况下也可以称作 边 (edge)。设 \(e = u \to v\)，则此时 \(u\) 称为 \(e\) 的 起点 (tail)，\(v\) 称为 \(e\) 的 终点 (head)，起点和终点也称为 \(e\) 的 端点 (endpoint)。并称 \(u\) 是 \(v\) 的直接前驱，\(v\) 是 \(u\) 的直接后继。

???+note "为什么起点是 tail，终点是 head？"
边通常用箭头表示，而箭头是从“尾”指向“头”的。

若 \(G\) 为混合图，则 \(E\) 中既有 有向边，又有 无向边。

若 \(G\) 的每条边 \(e_k=(u_k,v_k)\) 都被赋予一个数作为该边的 权，则称 \(G\) 为 赋权图。如果这些权都是正实数，就称 \(G\) 为 正权图。

图 \(G\) 的点数 \(\left| V(G) \right|\) 也被称作图 \(G\) 的 阶 (order)。

形象地说，图是由若干点以及连接点与点的边构成的。

相邻

在无向图 \(G = (V, E)\) 中，若点 \(v\) 是边 \(e\) 的一个端点，则称 \(v\) 和 \(e\) 是 关联的 (incident) 或 相邻的 (adjacent)。对于两顶点 \(u\) 和 \(v\)，若存在边 \((u, v)\)，则称 \(u\) 和 \(v\) 是 相邻的 (adjacent)。

一个顶点 \(v \in V\) 的 邻域 (neighborhood) 是所有与之相邻的顶点所构成的集合，记作 \(N(v)\)。

一个点集 \(S\) 的邻域是所有与 \(S\) 中至少一个点相邻的点所构成的集合，记作 \(N(S)\)，即：

\[N(S) = \bigcup_{v \in S} N(v) \]

度数

与一个顶点 \(v\) 关联的边的条数称作该顶点的 度 (degree)，记作 \(d(v)\)。特别地，对于边 \((v, v)\)，则每条这样的边要对 \(d(v)\) 产生 \(2\) 的贡献。

对于无向简单图，有 \(d(v) = \left| N(v) \right|\)。

握手定理（又称图论基本定理）：对于任何无向图 \(G = (V, E)\)，有 \(\sum_{v \in V} d(v) = 2 \left| E \right|\)。

推论：在任意图中，度数为奇数的点必然有偶数个。

若 \(d(v) = 0\)，则称 \(v\) 为 孤立点 (isolated vertex)。

若 \(d(v) = 1\)，则称 \(v\) 为 叶节点 (leaf vertex)/悬挂点 (pendant vertex)。

若 \(2 \mid d(v)\)，则称 \(v\) 为 偶点 (even vertex)。

若 \(2 \nmid d(v)\)，则称 \(v\) 为 奇点 (odd vertex)。图中奇点的个数是偶数。

若 \(d(v) = \left| V \right| - 1\)，则称 \(v\) 为 支配点 (universal vertex)。

对一张图，所有节点的度数的最小值称为 \(G\) 的 最小度 (minimum degree)，记作 \(\delta (G)\)；最大值称为 最大度 (maximum degree)，记作 \(\Delta (G)\)。即：\(\delta (G) = \min_{v \in G} d(v)\)，\(\Delta (G) = \max_{v \in G} d(v)\)。

在有向图 \(G = (V, E)\) 中，以一个顶点 \(v\) 为起点的边的条数称为该顶点的 出度 (out-degree)，记作 \(d^+(v)\)。以一个顶点 \(v\) 为终点的边的条数称为该节点的 入度 (in-degree)，记作 \(d^-(v)\)。显然 \(d^+(v)+d^-(v)=d(v)\)。

对于任何有向图 \(G = (V, E)\)，有：

\[\sum_{v \in V} d^+(v) = \sum_{v \in V} d^-(v) = \left| E \right| \]

若对一张无向图 \(G = (V, E)\)，每个顶点的度数都是一个固定的常数 \(k\)，则称 \(G\) 为 \(k\)- 正则图 (\(k\)-regular graph)。

如果给定一个序列 a，可以找到一个图 G，以其为度数列，则称 a 是 可图化 的。

如果给定一个序列 a，可以找到一个简单图 G，以其为度数列，则称 a 是 可简单图化 的。

简单图

自环 (loop)：对 \(E\) 中的边 \(e = (u, v)\)，若 \(u = v\)，则 \(e\) 被称作一个自环。

重边 (multiple edge)：若 \(E\) 中存在两个完全相同的元素（边）\(e_1, e_2\)，则它们被称作（一组）重边。

简单图 (simple graph)：若一个图中没有自环和重边，它被称为简单图。具有至少两个顶点的简单无向图中一定存在度相同的结点。（鸽巢原理）

如果一张图中有自环或重边，则称它为 多重图 (multigraph)。

!!! warning
在无向图中 \((u, v)\) 和 \((v, u)\) 算一组重边，而在有向图中，\(u \to v\) 和 \(v \to u\) 不为重边。

!!! warning
在题目中，如果没有特殊说明，是可以存在自环和重边的，在做题时需特殊考虑。

路径

途径 (walk)：途径是连接一连串顶点的边的序列，可以为有限或无限长度。形式化地说，一条有限途径 \(w\) 是一个边的序列 \(e_1, e_2, \ldots, e_k\)，使得存在一个顶点序列 \(v_0, v_1, \ldots, v_k\) 满足 \(e_i = (v_{i-1}, v_i)\)，其中 \(i \in [1, k]\)。这样的途径可以简写为 \(v_0 \to v_1 \to v_2 \to \cdots \to v_k\)。通常来说，边的数量 \(k\) 被称作这条途径的 长度（如果边是带权的，长度通常指途径上的边权之和，题目中也可能另有定义）。

迹 (trail)：对于一条途径 \(w\)，若 \(e_1, e_2, \ldots, e_k\) 两两互不相同，则称 \(w\) 是一条迹。

路径 (path)（又称 简单路径 (simple path))：对于一条迹 \(w\)，若其连接的点的序列中点两两不同，则称 \(w\) 是一条路径。

回路 (circuit)：对于一条迹 \(w\)，若 \(v_0 = v_k\)，则称 \(w\) 是一条回路。

环/圈 (cycle)（又称 简单回路/简单环 (simple circuit))：对于一条回路 \(w\)，若 \(v_0 = v_k\) 是点序列中唯一重复出现的点对，则称 \(w\) 是一个环。

!!! warning
关于路径的定义在不同地方可能有所不同，如，“路径”可能指本文中的“途径”，“环”可能指本文中的“回路”。如果在题目中看到类似的词汇，且没有“简单路径”/“非简单路径”（即本文中的“途径”）等特殊说明，最好询问一下具体指什么。

子图

对一张图 \(G = (V, E)\)，若存在另一张图 \(H = (V', E')\) 满足 \(V' \subseteq V\) 且 \(E' \subseteq E\)，则称 \(H\) 是 \(G\) 的 子图 (subgraph)，记作 \(H \subseteq G\)。

若对 \(H \subseteq G\)，满足 \(\forall u, v \in V'\)，只要 \((u, v) \in E\)，均有 \((u, v) \in E'\)，则称 \(H\) 是 \(G\) 的 导出子图/诱导子图 (induced subgraph)。

容易发现，一个图的导出子图仅由子图的点集决定，因此点集为 \(V'\)(\(V' \subseteq V\)) 的导出子图称为 \(V'\) 导出的子图，记作 \(G \left[ V' \right]\)。

若 \(H \subseteq G\) 满足 \(V' = V\)，则称 \(H\) 为 \(G\) 的 生成子图/支撑子图 (spanning subgraph)。

显然，\(G\) 是自身的子图，支撑子图，导出子图；无边图 是 \(G\) 的支撑子图。原图 \(G\) 和无边图都是 \(G\) 的平凡子图。

如果一张无向图 \(G\) 的某个生成子图 \(F\) 为 \(k\)- 正则图，则称 \(F\) 为 \(G\) 的一个 \(k\)- 因子 (\(k\)-factor)。

如果有向图 \(G = (V, E)\) 的导出子图 \(H = G \left[ V^\ast \right]\) 满足 \(\forall v \in V^\ast, (v, u) \in E\)，有 \(u \in V^\ast\)，则称 \(H\) 为 \(G\) 的一个 闭合子图 (closed subgraph)。

连通

无向图

对于一张无向图 \(G = (V, E)\)，对于 \(u, v \in V\)，若存在一条途径使得 \(v_0 = u, v_k = v\)，则称 \(u\) 和 \(v\) 是 连通的 (connected)。由定义，任意一个顶点和自身连通，任意一条边的两个端点连通。

若无向图 \(G = (V, E)\)，满足其中任意两个顶点均连通，则称 \(G\) 是 连通图 (connected graph)，\(G\) 的这一性质称作 连通性 (connectivity)。

若 \(H\) 是 \(G\) 的一个连通子图，且不存在 \(F\) 满足 \(H\subsetneq F \subseteq G\) 且 \(F\) 为连通图，则 \(H\) 是 \(G\) 的一个 连通块/连通分量 (connected component)（极大连通子图）。

有向图

对于一张有向图 \(G = (V, E)\)，对于 \(u, v \in V\)，若存在一条途径使得 \(v_0 = u, v_k = v\)，则称 \(u\) 可达 \(v\)。由定义，任意一个顶点可达自身，任意一条边的起点可达终点。（无向图中的连通也可以视作双向可达。）

若一张有向图的节点两两互相可达，则称这张图是 强连通的 (strongly connected)。

若一张有向图的边替换为无向边后可以得到一张连通图，则称原来这张有向图是 弱连通的 (weakly connected)。

与连通分量类似，也有 弱连通分量 (weakly connected component)（极大弱连通子图）和 强连通分量 (strongly connected component)（极大强连通子图）。

相关算法请参见 强连通分量。

割

相关算法请参见 割点和桥 以及 双连通分量。

在本部分中，有向图的“连通”一般指“强连通”。

对于连通图 \(G = (V, E)\)，若 \(V'\subseteq V\) 且 \(G\left[V\setminus V'\right]\)（即从 \(G\) 中删去 \(V'\) 中的点）不是连通图，则 \(V'\) 是图 \(G\) 的一个 点割集 (vertex cut/separating set)。大小为一的点割集又被称作 割点 (cut vertex)。

对于连通图 \(G = (V, E)\) 和整数 \(k\)，若 \(|V|\ge k+1\) 且 \(G\) 不存在大小为 \(k-1\) 的点割集，则称图 \(G\) 是 \(k\)- 点连通的 (\(k\)-vertex-connected)，而使得上式成立的最大的 \(k\) 被称作图 \(G\) 的 点连通度 (vertex connectivity)，记作 \(\kappa(G)\)。（对于非完全图，点连通度即为最小点割集的大小，而完全图 \(K_n\) 的点连通度为 \(n-1\)。）

对于图 \(G = (V, E)\) 以及 \(u, v\in V\) 满足 \(u\ne v\)，\(u\) 和 \(v\) 不相邻，\(u\) 可达 \(v\)，若 \(V'\subseteq V\)，\(u, v\notin V'\)，且在 \(G\left[V\setminus V'\right]\) 中 \(u\) 和 \(v\) 不连通，则 \(V'\) 被称作 \(u\) 到 \(v\) 的点割集。\(u\) 到 \(v\) 的最小点割集的大小被称作 \(u\) 到 \(v\) 的 局部点连通度 (local connectivity)，记作 \(\kappa(u, v)\)。

还可以在边上作类似的定义：

对于连通图 \(G = (V, E)\)，若 \(E'\subseteq E\) 且 \(G' = (V, E\setminus E')\)（即从 \(G\) 中删去 \(E'\) 中的边）不是连通图，则 \(E'\) 是图 \(G\) 的一个 边割集 (edge cut)。大小为一的边割集又被称作 桥 (bridge)。

对于连通图 \(G = (V, E)\) 和整数 \(k\)，若 \(G\) 不存在大小为 \(k-1\) 的边割集，则称图 \(G\) 是 \(k\)- 边连通的 (\(k\)-edge-connected)，而使得上式成立的最大的 \(k\) 被称作图 \(G\) 的 边连通度 (edge connectivity)，记作 \(\lambda(G)\)。（对于任何图，边连通度即为最小边割集的大小。）

对于图 \(G = (V, E)\) 以及 \(u, v\in V\) 满足 \(u\ne v\)，\(u\) 可达 \(v\)，若 \(E'\subseteq E\)，且在 \(G'=(V, E\setminus E')\) 中 \(u\) 和 \(v\) 不连通，则 \(E'\) 被称作 \(u\) 到 \(v\) 的边割集。\(u\) 到 \(v\) 的最小边割集的大小被称作 \(u\) 到 \(v\) 的 局部边连通度 (local edge-connectivity)，记作 \(\lambda(u, v)\)。

点双连通 (biconnected) 几乎与 \(2\)- 点连通完全一致，除了一条边连接两个点构成的图，它是点双连通的，但不是 \(2\)- 点连通的。换句话说，没有割点的连通图是点双连通的。

边双连通 (\(2\)-edge-connected) 与 \(2\)- 边双连通完全一致。换句话说，没有桥的连通图是边双连通的。

与连通分量类似，也有 点双连通分量 (biconnected component)（极大点双连通子图）和 边双连通分量 (\(2\)-edge-connected component)（极大边双连通子图）。

Whitney 定理：对任意的图 \(G\)，有 \(\kappa(G)\le \lambda(G)\le \delta(G)\)。（不等式中的三项分别为点连通度、边连通度、最小度。）

稀疏图/稠密图

若一张图的边数远小于其点数的平方，那么它是一张 稀疏图 (sparse graph)。

若一张图的边数接近其点数的平方，那么它是一张 稠密图 (dense graph)。

这两个概念并没有严格的定义，一般用于讨论 时间复杂度 为 \(O(|V|^2)\) 的算法与 \(O(|E|)\) 的算法的效率差异（在稠密图上这两种算法效率相当，而在稀疏图上 \(O(|E|)\) 的算法效率明显更高）。

补图

对于无向简单图 \(G = (V, E)\)，它的 补图 (complement graph) 指的是这样的一张图：记作 \(\bar G\)，满足 \(V \left( \bar G \right) = V \left( G \right)\)，且对任意节点对 \((u, v)\)，\((u, v) \in E \left( \bar G \right)\) 当且仅当 \((u, v) \notin E \left( G \right)\)。

反图

对于有向图 \(G = (V, E)\)，它的 反图 (transpose graph) 指的是点集不变，每条边反向得到的图，即：若 \(G\) 的反图为 \(G'=(V, E')\)，则 \(E'=\{(v, u)|(u, v)\in E\}\)。

特殊的图

若无向简单图 \(G\) 满足任意不同两点间均有边，则称 \(G\) 为 完全图 (complete graph)，\(n\) 阶完全图记作 \(K_n\)。若有向图 \(G\) 满足任意不同两点间都有两条方向不同的边，则称 \(G\) 为 有向完全图 (complete digraph)。

边集为空的图称为 无边图 (edgeless graph)、空图 (empty graph) 或 零图 (null graph)，\(n\) 阶无边图记作 \(\overline{K}_n\) 或 \(N_n\)。\(N_n\) 与 \(K_n\) 互为补图。

!!! warning
零图 (null graph) 也可指 零阶图 (order-zero graph) \(K_0\)，即点集与边集均为空的图。

若有向简单图 \(G\) 满足任意不同两点间都有恰好一条边（单向），则称 \(G\) 为 竞赛图 (tournament graph)。

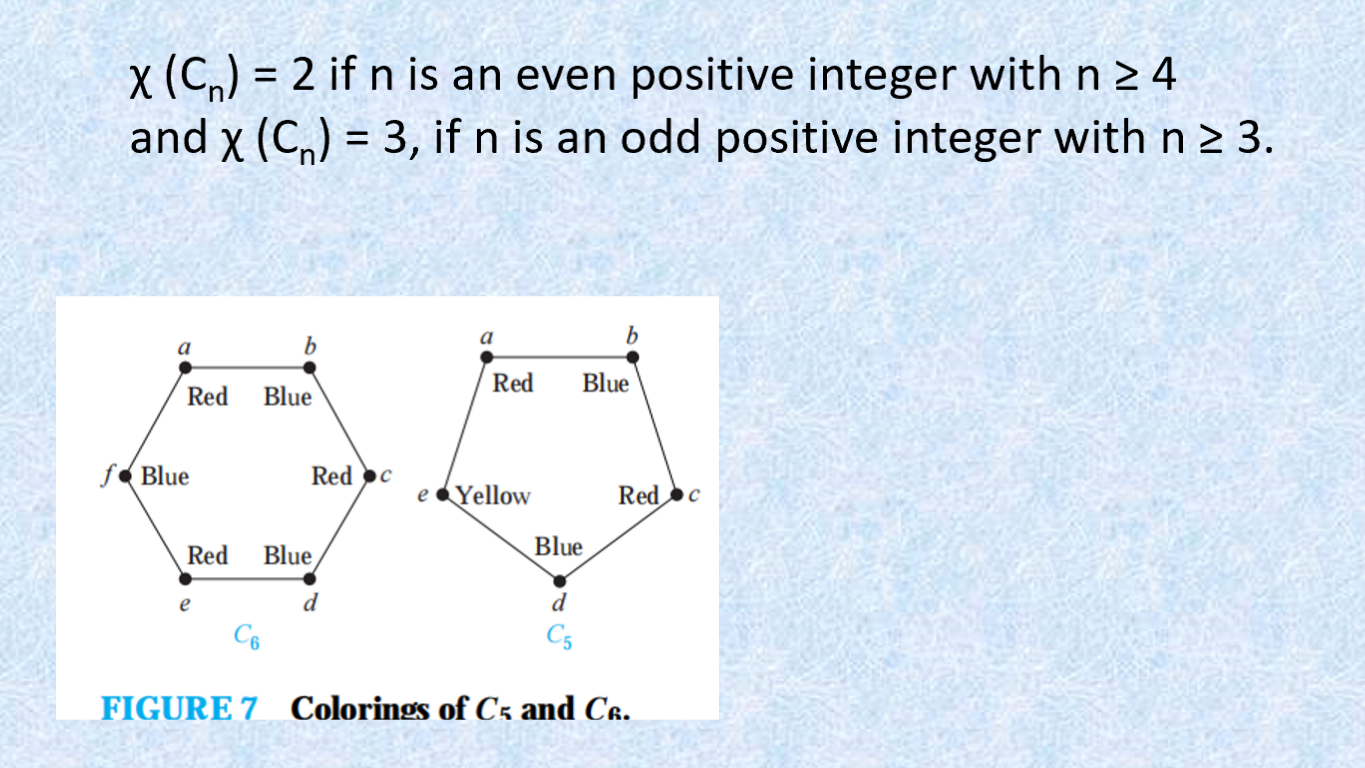
若无向简单图 \(G = \left( V, E \right)\) 的所有边恰好构成一个圈，则称 \(G\) 为 环图/圈图 (cycle graph)，\(n\)(\(n \geq 3\)) 阶圈图记作 \(C_n\)。易知，一张图为圈图的充分必要条件是，它是 \(2\)- 正则连通图。

若无向简单图 \(G = \left( V, E \right)\) 满足，存在一个点 \(v\) 为支配点，其余点之间没有边相连，则称 \(G\) 为 星图/菊花图 (star graph)，\(n + 1\)(\(n \geq 1\)) 阶星图记作 \(S_n\)。

若无向简单图 \(G = \left( V, E \right)\) 满足，存在一个点 \(v\) 为支配点，其它点之间构成一个圈，则称 \(G\) 为 轮图 (wheel graph)，\(n + 1\)(\(n \geq 3\)) 阶轮图记作 \(W_n\)。

若无向简单图 \(G = \left( V, E \right)\) 的所有边恰好构成一条简单路径，则称 \(G\) 为 链 (chain/path graph)，\(n\) 阶的链记作 \(P_n\)。易知，一条链由一个圈图删去一条边而得。

如果一张无向连通图不含环，则称它是一棵 树 (tree)。相关内容详见 树基础。

如果一张无向连通图包含恰好一个环，则称它是一棵 基环树 (pseudotree)。

如果一张有向弱连通图每个点的入度都为 \(1\)，则称它是一棵 基环外向树。

如果一张有向弱连通图每个点的出度都为 \(1\)，则称它是一棵 基环内向树。

多棵树可以组成一个 森林 (forest)，多棵基环树可以组成 基环森林 (pseudoforest)，多棵基环外向树可以组成 基环外向树森林，多棵基环内向树可以组成 基环内向森林 (functional graph)。

如果一张无向连通图的每条边最多在一个环内，则称它是一棵 仙人掌 (cactus)。多棵仙人掌可以组成 沙漠。

如果一张图的点集可以被分为两部分，每一部分的内部都没有连边，那么这张图是一张 二分图 (bipartite graph)。如果二分图中任何两个不在同一部分的点之间都有连边，那么这张图是一张 完全二分图 (complete bipartite graph/biclique)，一张两部分分别有 \(n\) 个点和 \(m\) 个点的完全二分图记作 \(K_{n, m}\)。相关内容详见 二分图。

如果一张图可以画在一个平面上，且没有两条边在非端点处相交，那么这张图是一张 平面图 (planar graph)。一张图的任何子图都不是 \(K_5\) 或 \(K_{3, 3}\) 是其为一张平面图的充要条件。对于简单连通平面图 \(G=(V, E)\) 且 \(V\ge 3\)，\(|E|\le 3|V|-6\)。

同构

两个图 \(G\) 和 \(H\)，如果存在一个双射 \(f : V(G) \to V(H)\)，且满足 \((u,v)\in E(G)\)，当且仅当 \((f(u),f(v))\in E(H)\)，则我们称 \(f\) 为 \(G\) 到 \(H\) 的一个 同构 (isomorphism)，且图 \(G\) 与图 \(H\) 是 同构的 (isomorphic)，记作 \(G \cong H\)。

从定义可知，若 \(G \cong H\)，必须满足：

• \(|V(G)|=|V(H)|,|E(G)|=|E(H)|\)
• \(G\) 和 \(H\) 结点度的非增序列相同
• \(G\) 和 \(H\) 存在同构的导出子图

无向简单图的二元运算

对于无向简单图，我们可以定义如下二元运算：

交 (intersection)：图 \(G = \left( V_1, E_1 \right), H = \left( V_2, E_2 \right)\) 的交定义成图 \(G \cap H = \left( V_1 \cap V_2, E_1 \cap E_2 \right)\)。

容易证明两个无向简单图的交还是无向简单图。

并 (union)：图 \(G = \left( V_1, E_1 \right), H = \left( V_2, E_2 \right)\) 的并定义成图 \(G \cup H = \left( V_1 \cup V_2, E_1 \cup E_2 \right)\)。

和 (sum)/直和 (direct sum)：对于 \(G = \left( V_1, E_1 \right), H = \left( V_2, E_2 \right)\)，任意构造 \(H' \cong H\) 使得 \(V \left( H' \right) \cap V_1 = \varnothing\)(\(H'\) 可以等于 \(H\))。此时与 \(G \cup H'\) 同构的任何图称为 \(G\) 和 \(H\) 的和/直和/不交并，记作 \(G + H\) 或 \(G \oplus H\)。

若 \(G\) 与 \(H\) 的点集本身不相交，则 \(G \cup H = G + H\)。

比如，森林可以定义成若干棵树的和。

???+note "并与和的区别"
可以理解为，“并”会让两张图中“名字相同”的点、边合并，而“和”则不会。

特殊的点集/边集

支配集

对于无向图 \(G=(V, E)\)，若 \(V'\subseteq V\) 且 \(\forall v\in(V\setminus V')\) 存在边 \((u, v)\in E\) 满足 \(u\in V'\)，则 \(V'\) 是图 \(G\) 的一个 支配集 (dominating set)。

无向图 \(G\) 最小的支配集的大小记作 \(\gamma(G)\)。求一张图的最小支配集是 NP 困难 的。

对于有向图 \(G=(V, E)\)，若 \(V'\subseteq V\) 且 \(\forall v\in(V\setminus V')\) 存在边 \((u, v)\in E\) 满足 \(u\in V'\)，则 \(V'\) 是图 \(G\) 的一个 出 - 支配集 (out-dominating set)。类似地，可以定义有向图的 入 - 支配集 (in-dominating set)。

有向图 \(G\) 最小的出 - 支配集大小记作 \(\gamma^+(G)\)，最小的入 - 支配集大小记作 \(\gamma^-(G)\)。

边支配集

对于图 \(G=(V, E)\)，若 \(E'\subseteq E\) 且 \(\forall e\in(E\setminus E')\) 存在 \(E'\) 中的边与其有公共点，则称 \(E'\) 是图 \(G\) 的一个 边支配集 (edge dominating set)。

求一张图的最小边支配集是 NP 困难 的。

独立集

对于图 \(G=(V, E)\)，若 \(V'\subseteq V\) 且 \(V'\) 中任意两点都不相邻，则 \(V'\) 是图 \(G\) 的一个 独立集 (independent set)。

图 \(G\) 最大的独立集的大小记作 \(\alpha(G)\)。求一张图的最大独立集是 NP 困难 的。

匹配

对于图 \(G=(V, E)\)，若 \(E'\in E\) 且 \(E'\) 中任意两条不同的边都没有公共的端点，且 \(E'\) 中任意一条边都不是自环，则 \(E'\) 是图 \(G\) 的一个 匹配 (matching)，也可以叫作 边独立集 (independent edge set)。如果一个点是匹配中某条边的一个端点，则称这个点是 被匹配的 (matched)/饱和的 (saturated)，否则称这个点是 不被匹配的 (unmatched)。

边数最多的匹配被称作一张图的 最大匹配 (maximum-cardinality matching)。图 \(G\) 的最大匹配的大小记作 \(\nu(G)\)。

如果边带权，那么权重之和最大的匹配被称作一张图的 最大权匹配 (maximum-weight matching)。

如果一个匹配在加入任何一条边后都不再是一个匹配，那么这个匹配是一个 极大匹配 (maximal matching)。最大的极大匹配就是最大匹配，任何最大匹配都是极大匹配。极大匹配一定是边支配集，但边支配集不一定是匹配。最小极大匹配和最小边支配集大小相等，但最小边支配集不一定是匹配。求最小极大匹配是 NP 困难的。

如果在一个匹配中所有点都是被匹配的，那么这个匹配是一个 完美匹配 (perfect matching)。如果在一个匹配中只有一个点不被匹配，那么这个匹配是一个 准完美匹配 (near-perfect matching)。

求一张普通图或二分图的匹配或完美匹配个数都是 #P 完全 的。

对于一个匹配 \(M\)，若一条路径以非匹配点为起点，每相邻两条边的其中一条在匹配中而另一条不在匹配中，则这条路径被称作一条 交替路径 (alternating path)；一条在非匹配点终止的交替路径，被称作一条 增广路径 (augmenting path)。

托特定理：\(n\) 阶无向图 \(G\) 有完美匹配当且仅当对于任意的 \(V' \subset V(G)\)，\(p_{\text{奇}}(G-V')\leq |V'|\)，其中 \(p_{\text{奇}}\) 表示奇数阶连通分支数。

托特定理（推论）：任何无桥 3 - 正则图都有完美匹配。

点覆盖

对于图 \(G=(V, E)\)，若 \(V'\subseteq V\) 且 \(\forall e\in E\) 满足 \(e\) 的至少一个端点在 \(V'\) 中，则称 \(V'\) 是图 \(G\) 的一个 点覆盖 (vertex cover)。

点覆盖集必为支配集，但极小点覆盖集不一定是极小支配集。

一个点集是点覆盖的充要条件是其补集是独立集，因此最小点覆盖的补集是最大独立集。求一张图的最小点覆盖是 NP 困难 的。

一张图的任何一个匹配的大小都不超过其任何一个点覆盖的大小。完全二分图 \(K_{n, m}\) 的最大匹配和最小点覆盖大小都为 \(\min(n, m)\)。

边覆盖

对于图 \(G=(V, E)\)，若 \(E'\subseteq E\) 且 \(\forall v\in V\) 满足 \(v\) 与 \(E'\) 中的至少一条边相邻，则称 \(E'\) 是图 \(G\) 的一个 边覆盖 (edge cover)。

最小边覆盖的大小记作 \(\rho(G)\)，可以由最大匹配贪心扩展求得：对于所有非匹配点，将其一条邻边加入最大匹配中，即得到了一个最小边覆盖。

最大匹配也可以由最小边覆盖求得：对于最小边覆盖中每对有公共点的边删去其中一条。

一张图的最小边覆盖的大小加上最大匹配的大小等于图的点数，即 \(\rho(G)+\nu(G)=|V(G)|\)。

一张图的最大匹配的大小不超过最小边覆盖的大小，即 \(\nu(G)\le\rho(G)\)。特别地，完美匹配一定是一个最小边覆盖，这也是上式取到等号的唯一情况。

一张图的任何一个独立集的大小都不超过其任何一个边覆盖的大小。完全二分图 \(K_{n, m}\) 的最大独立集和最小边覆盖大小都为 \(\max(n, m)\)。

团

对于图 \(G=(V, E)\)，若 \(V'\subseteq V\) 且 \(V'\) 中任意两个不同的顶点都相邻，则 \(V'\) 是图 \(G\) 的一个 团 (clique)。团的导出子图是完全图。

如果一个团在加入任何一个顶点后都不再是一个团，则这个团是一个 极大团 (maximal clique)。

一张图的最大团的大小记作 \(\omega(G)\)，最大团的大小等于其补图最大独立集的大小，即 \(\omega(G)=\alpha(\bar{G})\)。求一张图的最大团是 NP 困难 的。

强连通

在阅读下列内容之前，请务必了解 图论相关概念 中的基础部分。

强连通的定义是：有向图 G 强连通是指，G 中任意两个结点连通。

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图。

这里要介绍的是如何来求强连通分量。

Tarjan 算法

引入

Robert E. Tarjan（罗伯特·塔扬，1948~），生于美国加州波莫纳，计算机科学家。

Tarjan 发明了很多算法和数据结构。不少他发明的算法都以他的名字命名，以至于有时会让人混淆几种不同的算法。比如求各种连通分量的 Tarjan 算法，求 LCA（Lowest Common Ancestor，最近公共祖先）的 Tarjan 算法。并查集、Splay、Toptree 也是 Tarjan 发明的。

我们这里要介绍的是在有向图中求强连通分量的 Tarjan 算法。

DFS 生成树

在介绍该算法之前，先来了解 DFS 生成树，我们以下面的有向图为例：

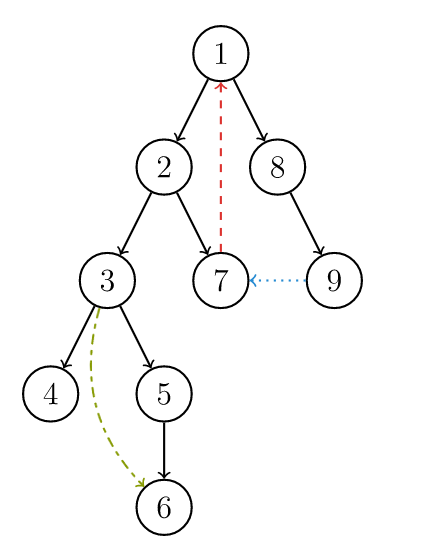
有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：

1. 树边（tree edge）：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
2. 反祖边（back edge）：示意图中以红色边表示（即 \(7 \rightarrow 1\)），也被叫做回边，即指向祖先结点的边。
3. 横叉边（cross edge）：示意图中以蓝色边表示（即 \(9 \rightarrow 7\)），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。
4. 前向边（forward edge）：示意图中以绿色边表示（即 \(3 \rightarrow 6\)），它是在搜索的时候遇到子树中的结点的时候形成的。

我们考虑 DFS 生成树与强连通分量之间的关系。

如果结点 \(u\) 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 \(u\) 为根的子树中。结点 \(u\) 被称为这个强连通分量的根。

反证法：假设有个结点 \(v\) 在该强连通分量中但是不在以 \(u\) 为根的子树中，那么 \(u\) 到 \(v\) 的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和 \(u\) 是第一个访问的结点矛盾了。得证。

Tarjan 算法求强连通分量

在 Tarjan 算法中为每个结点 \(u\) 维护了以下几个变量：

1. \(\textit{dfn}_u\)：深度优先搜索遍历时结点 \(u\) 被搜索的次序。
2. \(\textit{low}_u\)：在 \(u\) 的子树中能够回溯到的最早的已经在栈中的结点。设以 \(u\) 为根的子树为 \(\textit{Subtree}_u\)。\(\textit{low}_u\) 定义为以下结点的 \(\textit{dfn}\) 的最小值：\(\textit{Subtree}_u\) 中的结点；从 \(\textit{Subtree}_u\) 通过一条不在搜索树上的边能到达的结点。

一个结点的子树内结点的 dfn 都大于该结点的 dfn。

从根开始的一条路径上的 dfn 严格递增，low 严格非降。

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索，维护每个结点的 dfn 与 low 变量，且让搜索到的结点入栈。每当找到一个强连通元素，就按照该元素包含结点数目让栈中元素出栈。在搜索过程中，对于结点 \(u\) 和与其相邻的结点 \(v\)（\(v\) 不是 \(u\) 的父节点）考虑 3 种情况：

1. \(v\) 未被访问：继续对 \(v\) 进行深度搜索。在回溯过程中，用 \(\textit{low}_v\) 更新 \(\textit{low}_u\)。因为存在从 \(u\) 到 \(v\) 的直接路径，所以 \(v\) 能够回溯到的已经在栈中的结点，\(u\) 也一定能够回溯到。
2. \(v\) 被访问过，已经在栈中：根据 low 值的定义，用 \(\textit{dfn}_v\) 更新 \(\textit{low}_u\)。
3. \(v\) 被访问过，已不在栈中：说明 \(v\) 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

将上述算法写成伪代码：

???+note "实现"
text TARJAN_SEARCH(int u) vis[u]=true low[u]=dfn[u]=++dfncnt push u to the stack for each (u,v) then do if v hasn't been searched then TARJAN_SEARCH(v) // 搜索 low[u]=min(low[u],low[v]) // 回溯 else if v has been in the stack then low[u]=min(low[u],dfn[v])

对于一个连通分量图，我们很容易想到，在该连通图中有且仅有一个 \(u\) 使得 \(\textit{dfn}_u=\textit{low}_u\)。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 dfn 和 low 值最小，不会被该连通分量中的其他结点所影响。

因此，在回溯的过程中，判定 \(\textit{dfn}_u=\textit{low}_u\) 是否成立，如果成立，则栈中 \(u\) 及其上方的结点构成一个 SCC。

实现

=== "C++"

```cpp
int dfn[N], low[N], dfncnt, s[N], in_stack[N], tp;
int scc[N], sc;  // 结点 i 所在 SCC 的编号
int sz[N];       // 强连通 i 的大小

void tarjan(int u) {
  low[u] = dfn[u] = ++dfncnt, s[++tp] = u, in_stack[u] = 1;
  for (int i = h[u]; i; i = e[i].nex) {
    const int &v = e[i].t;
    if (!dfn[v]) {
      tarjan(v);
      low[u] = min(low[u], low[v]);
    } else if (in_stack[v]) {
      low[u] = min(low[u], dfn[v]);
    }
  }
  if (dfn[u] == low[u]) {
    ++sc;
    while (s[tp] != u) {
      scc[s[tp]] = sc;
      sz[sc]++;
      in_stack[s[tp]] = 0;
      --tp;
    }
    scc[s[tp]] = sc;
    sz[sc]++;
    in_stack[s[tp]] = 0;
    --tp;
  }
}
```

=== "Python"

```python
dfn = [] * N; low = [] * N; dfncnt = 0; s = [] * N; in_stack  = [] * N; tp = 0
scc = [] * N; sc = 0 # 结点 i 所在 SCC 的编号
sz = [] * N # 强连通 i 的大小
def tarjan(u):
    low[u] = dfn[u] = dfncnt; s[tp] = u; in_stack[u] = 1
    dfncnt = dfncnt + 1; tp = tp + 1
    i = h[u]
    while i:
        v = e[i].t
        if dfn[v] == False:
            tarjan(v)
            low[u] = min(low[u], low[v])
        elif in_stack[v]:
            low[u] = min(low[u], dfn[v])
        i = e[i].nex
    if dfn[u] == low[u]:
        sc = sc + 1
        while s[tp] != u:
            scc[s[tp]] = sc
            sz[sc] = sz[sc] + 1
            in_stack[s[tp]] = 0
            tp = tp - 1
        scc[s[tp]] = sc
        sz[sc] = sz[sc] + 1
        in_stack[s[tp]] = 0
        tp = tp - 1
```

时间复杂度 \(O(n + m)\)。

Kosaraju 算法

引入

Kosaraju 算法最早在 1978 年由 S. Rao Kosaraju 在一篇未发表的论文上提出，但 Micha Sharir 最早发表了它。

过程

该算法依靠两次简单的 DFS 实现：

第一次 DFS，选取任意顶点作为起点，遍历所有未访问过的顶点，并在回溯之前给顶点编号，也就是后序遍历。

第二次 DFS，对于反向后的图，以标号最大的顶点作为起点开始 DFS。这样遍历到的顶点集合就是一个强连通分量。对于所有未访问过的结点，选取标号最大的，重复上述过程。

两次 DFS 结束后，强连通分量就找出来了，Kosaraju 算法的时间复杂度为 \(O(n+m)\)。

实现

=== "C++"

```cpp
// g 是原图，g2 是反图

void dfs1(int u) {
  vis[u] = true;
  for (int v : g[u])
    if (!vis[v]) dfs1(v);
  s.push_back(u);
}

void dfs2(int u) {
  color[u] = sccCnt;
  for (int v : g2[u])
    if (!color[v]) dfs2(v);
}

void kosaraju() {
  sccCnt = 0;
  for (int i = 1; i <= n; ++i)
    if (!vis[i]) dfs1(i);
  for (int i = n; i >= 1; --i)
    if (!color[s[i]]) {
      ++sccCnt;
      dfs2(s[i]);
    }
}
```

=== "Python"

```python
def dfs1(u):
    vis[u] = True
    for v in g[u]:
        if vis[v] == False:
            dfs1(v)
    s.append(u)

def dfs2(u):
    color[u] = sccCnt
    for v in g2[u]:
        if color[v] == False:
            dfs2(v)

def kosaraju(u):
    sccCnt = 0
    for i in range(1, n + 1):
        if vis[i] == False:
            dfs1(i)
    for i in range(n, 0, -1):
        if color[s[i]] == False:
            sccCnt = sccCnt + 1
            dfs2(s[i])
```

Garbow 算法

过程

Garbow 算法是 Tarjan 算法的另一种实现，Tarjan 算法是用 dfn 和 low 来计算强连通分量的根，Garbow 维护一个节点栈，并用第二个栈来确定何时从第一个栈中弹出属于同一个强连通分量的节点。从节点 \(w\) 开始的 DFS 过程中，当一条路径显示这组节点都属于同一个强连通分量时，只要栈顶节点的访问时间大于根节点 \(w\) 的访问时间，就从第二个栈中弹出这个节点，那么最后只留下根节点 \(w\)。在这个过程中每一个被弹出的节点都属于同一个强连通分量。

当回溯到某一个节点 \(w\) 时，如果这个节点在第二个栈的顶部，就说明这个节点是强连通分量的起始节点，在这个节点之后搜索到的那些节点都属于同一个强连通分量，于是从第一个栈中弹出那些节点，构成强连通分量。

实现

=== "C++"

```cpp
int garbow(int u) {
  stack1[++p1] = u;
  stack2[++p2] = u;
  low[u] = ++dfs_clock;
  for (int i = head[u]; i; i = e[i].next) {
    int v = e[i].to;
    if (!low[v])
      garbow(v);
    else if (!sccno[v])
      while (low[stack2[p2]] > low[v]) p2--;
  }
  if (stack2[p2] == u) {
    p2--;
    scc_cnt++;
    do {
      sccno[stack1[p1]] = scc_cnt;
      // all_scc[scc_cnt] ++;
    } while (stack1[p1--] != u);
  }
  return 0;
}

void find_scc(int n) {
  dfs_clock = scc_cnt = 0;
  p1 = p2 = 0;
  memset(sccno, 0, sizeof(sccno));
  memset(low, 0, sizeof(low));
  for (int i = 1; i <= n; i++)
    if (!low[i]) garbow(i);
}
```

=== "Python"

```python
def garbow(u):
    stack1[p1] = u
    stack2[p2] = u
    p1 = p1 + 1; p2 = p2 + 1
    low[u] = dfs_clock
    dfs_clock = dfs_clock + 1
    i = head[u]
    while i:
        v = e[i].to
        if low[v] == False:
            garbow(v)
        elif sccno[v] == False:
            while low[stack2[p2]] > low[v]:
                p2 = p2 - 1
    if stack2[p2] == u:
        p2 = p2 - 1
        scc_cnt = scc_cnt + 1
        while stack1[p1] != u:
            p1 = p1 - 1
            sccno[stack1[p1]] = scc_cnt

def find_scc(n):
    dfs_clock = scc_cnt = 0
    p1 = p2 = 0
    sccno = []; low = []
    for i in range(1, n + 1):
        if low[i] == False:
            garbow(i)
```

应用

我们可以将一张图的每个强连通分量都缩成一个点。

然后这张图会变成一个 DAG，可以进行拓扑排序以及更多其他操作。

举个简单的例子，求一条路径，可以经过重复结点，要求经过的不同结点数量最多。

双连通分量

定义

在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 边双连通。

在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪个点（只能删去一个，且不能删 \(u\) 和 \(v\) 自己）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 点双连通。

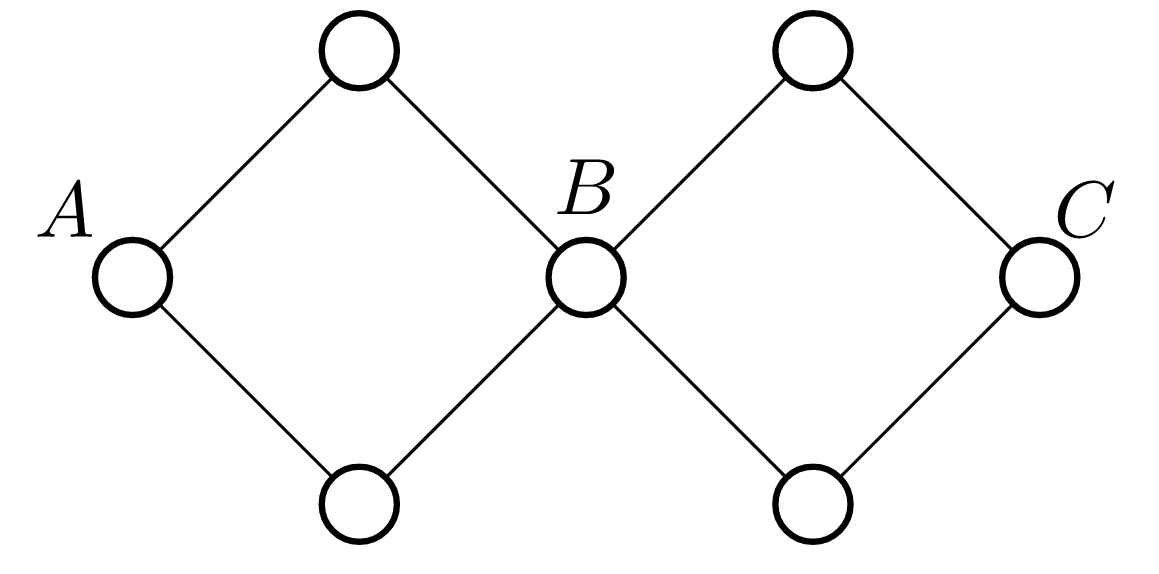
边双连通具有传递性，即，若 \(x,y\) 边双连通，\(y,z\) 边双连通，则 \(x,z\) 边双连通。

点双连通 不 具有传递性，反例如下图，\(A,B\) 点双连通，\(B,C\) 点双连通，而 \(A,C\) 不 点双连通。

DFS

对于一张连通的无向图，我们可以从任意一点开始 DFS，得到原图的一棵生成树（以开始 DFS 的那个点为根），这棵生成树上的边称作 树边，不在生成树上的边称作 非树边。

由于 DFS 的性质，我们可以保证所有非树边连接的两个点在生成树上都满足其中一个是另一个的祖先。

DFS 的代码如下：

???+note "实现"
=== "C++"

    ```cpp
    void DFS(int p) {
      visited[p] = true;
      for (int to : edge[p])
        if (!visited[to]) DFS(to);
    }
    ```

=== "Python"

    ```python
    def DFS(p):
        visited[p] = True
        for to in edge[p]:
            if visited[to] == False:
                DFS(to)
    ```

过程

DFS 找桥并判断边双连通

首先，对原图进行 DFS。

如上图所示，黑色与绿色边为树边，红色边为非树边。每一条非树边连接的两个点都对应了树上的一条简单路径，我们说这条非树边 覆盖 了这条树上路径上所有的边。绿色的树边 至少 被一条非树边覆盖，黑色的树边不被 任何 非树边覆盖。

我们如何判断一条边是不是桥呢？显然，非树边和绿色的树边一定不是桥，黑色的树边一定是桥。

如何用算法去实现以上过程呢？首先有一个比较暴力的做法，对于每一条非树边，都逐个地将它覆盖的每一条树边置成绿色，这样的时间复杂度为 \(O(nm)\)。

怎么优化呢？可以用差分。对于每一条非树边，在其树上深度较小的点处打上 -1 标记，在其树上深度较大的点处打上 +1 标记。然后 \(O(n)\) 求出每个点的子树内部的标记之和。对于一个点 \(u\)，其子树内部的标记之和等于覆盖了 \(u\) 和 \(u\) 的父亲之间的树边的非树边数量。若这个值非 \(0\)，则 \(u\) 和 \(u\) 的父亲之间的树边不是桥，否则是桥。

用以上的方法 \(O(n+m)\) 求出每条边分别是否是桥后，两个点是边双连通的，当且仅当它们的树上路径中 不 包含桥。

DFS 找割点并判断点双连通

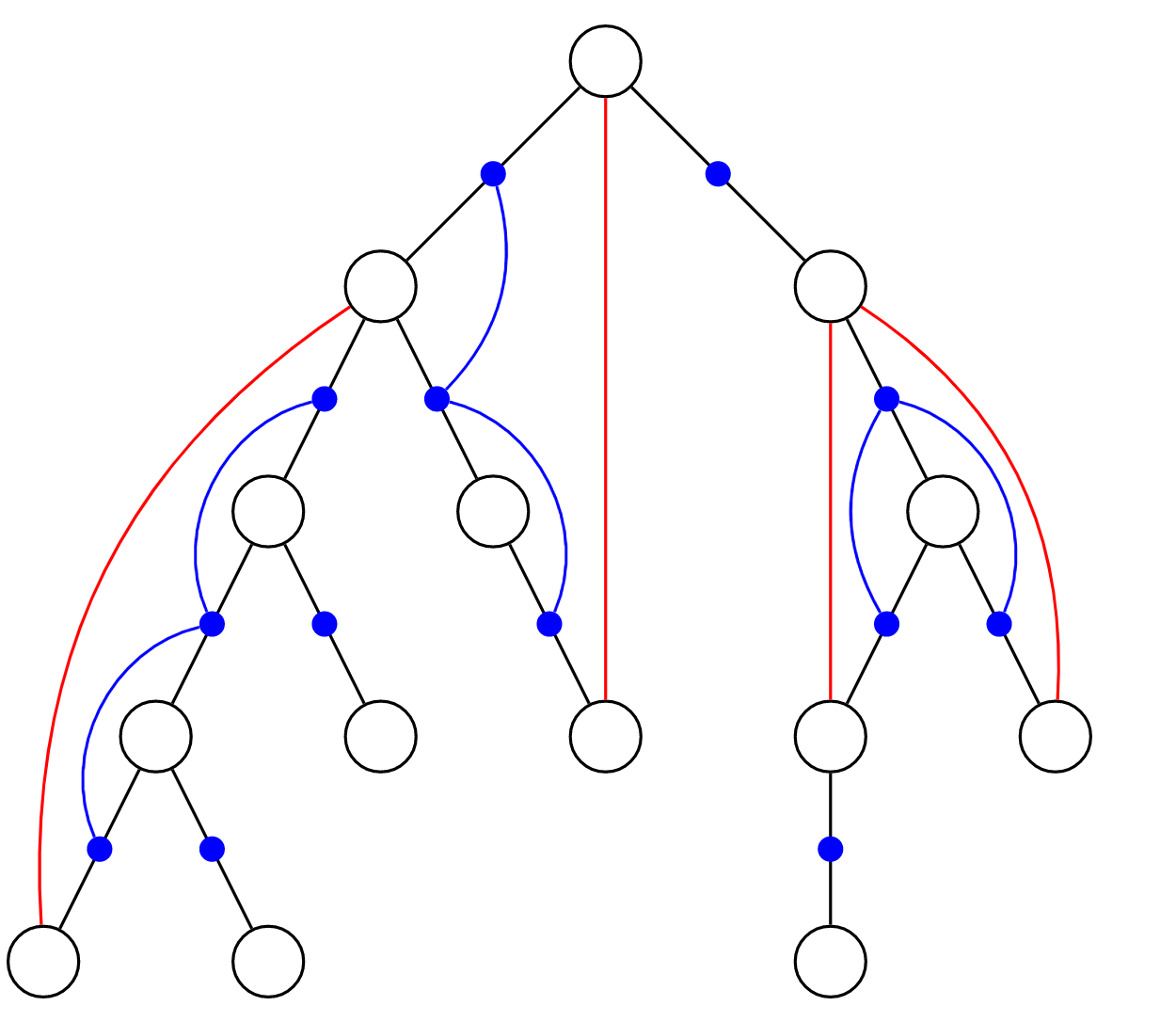
如上图所示，黑色边为树边，红色边为非树边。每一条非树边连接的两个点都对应了树上的一条简单路径。

考虑一张新图，新图中的每一个点对应原图中的每一条树边（在上图中用蓝色点表示）。对于原图中的每一条非树边，将这条非树边对应的树上简单路径中的所有边在新图中对应的蓝点连成一个连通块（这在上图中也用蓝色的边体现出来了）。

这样，一个点不是割点，当且仅当与其相连的所有边在新图中对应的蓝点都属于同一个连通块。两个点点双连通，当且仅当它们在原图的树上路径中的所有边在新图中对应的蓝点都属于同一个连通块。

蓝点间的连通关系可以用与求边双连通时用到的差分类似的方法维护，时间复杂度 \(O(n+m)\)。

author: Ir1d, sshwy, GavinZhengOI, Planet6174, ouuan, Marcythm, ylxmf2005, 0xis-cn

相关阅读：双连通分量，

割点和桥更严谨的定义参见 图论相关概念。

割点

对于一个无向图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点（又称割顶）。

过程

如果我们尝试删除每个点，并且判断这个图的连通性，那么复杂度会特别的高。所以要介绍一个常用的算法：Tarjan。

首先，我们上一个图：

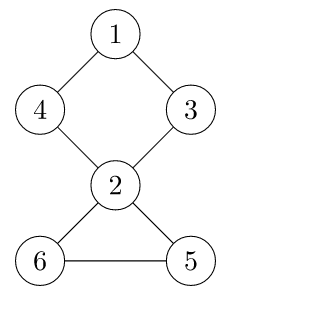
很容易的看出割点是 2，而且这个图仅有这一个割点。

首先，我们按照 DFS 序给他打上时间戳（访问的顺序）。

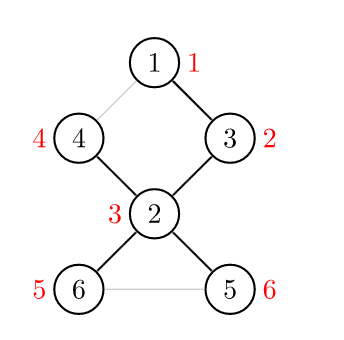
这些信息被我们保存在一个叫做 num 的数组中。

还需要另外一个数组 low，用它来存储不经过其父亲能到达的最小的时间戳。

例如 low[2] 的话是 1，low[5] 和 low[6] 是 3。

然后我们开始 DFS，我们判断某个点是否是割点的根据是：对于某个顶点 \(u\)，如果存在至少一个顶点 \(v\)（\(u\) 的儿子），使得 \(low_v \geq num_u\)，即不能回到祖先，那么 \(u\) 点为割点。

此根据惟独不适用于搜索的起始点，其需要特殊考虑：若该点不是割点，则其他路径亦能到达全部结点，因此从起始点只「向下搜了一次」，即在搜索树内仅有一个子结点。如果在搜索树内有两个及以上的儿子，那么他一定是割点了（设想上图从 2 开始搜索，搜索树内应有两个子结点：3 或 4 及 5 或 6）。如果只有一个儿子，那么把它删掉，不会有任何的影响。比如下面这个图，此处形成了一个环。

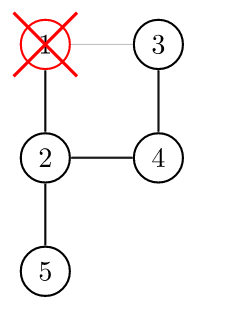
我们在访问 1 的儿子时候，假设先 DFS 到了 2，然后标记用过，然后递归往下，来到了 4，4 又来到了 3，当递归回溯的时候，会发现 3 已经被访问过了，所以不是割点。

更新 low 的伪代码如下：

如果 v 是 u 的儿子 low[u] = min(low[u], low[v]);
否则
low[u] = min(low[u], num[v]);

割边

和割点差不多，叫做桥。

对于一个无向图，如果删掉一条边后图中的连通分量数增加了，则称这条边为桥或者割边。严谨来说，就是：假设有连通图 \(G=\{V,E\}\)，\(e\) 是其中一条边（即 \(e \in E\)），如果 \(G-e\) 是不连通的，则边 \(e\) 是图 \(G\) 的一条割边（桥）。

比如说，下图中，

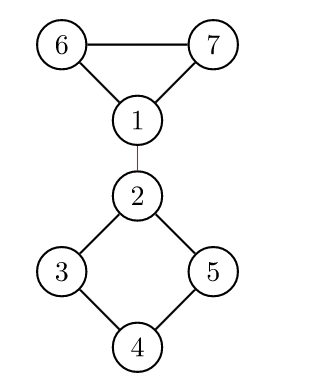
红色的边就是割边。

过程

和割点差不多，只要改一处：\(low_v>num_u\) 就可以了，而且不需要考虑根节点的问题。

割边是和是不是根节点没关系的，原来我们求割点的时候是指点 \(v\) 是不可能不经过父节点 \(u\) 为回到祖先节点（包括父节点），所以顶点 \(u\) 是割点。如果 \(low_v=num_u\) 表示还可以回到父节点，如果顶点 \(v\) 不能回到祖先也没有另外一条回到父亲的路，那么 \(u-v\) 这条边就是割边。

实现

下面代码实现了求割边，其中，当 isbridge[x] 为真时，(father[x],x) 为一条割边。

=== "C++"

```cpp
int low[MAXN], dfn[MAXN], dfs_clock;
bool isbridge[MAXN];
vector<int> G[MAXN];
int cnt_bridge;
int father[MAXN];

void tarjan(int u, int fa) {
  father[u] = fa;
  low[u] = dfn[u] = ++dfs_clock;
  for (int i = 0; i < G[u].size(); i++) {
    int v = G[u][i];
    if (!dfn[v]) {
      tarjan(v, u);
      low[u] = min(low[u], low[v]);
      if (low[v] > dfn[u]) {
        isbridge[v] = true;
        ++cnt_bridge;
      }
    } else if (dfn[v] < dfn[u] && v != fa) {
      low[u] = min(low[u], dfn[v]);
    }
  }
}
```

=== "Python"

```python
low = [] * MAXN; dfn = [] * MAXN; dfs_clock = 0
isbridge = [False] * MAXN
G = [[0 for i in range(MAXN)] for j in range(MAXN)]
cnt_bridge = 0
father = [] * MAXN

def tarjan(u, fa):
    father[u] = fa
    low[u] = dfn[u] = dfs_clock
    dfs_clock = dfs_clock + 1
    for i in range(0, len(G[u])):
        v = G[u][i]
        if dfn[v] == False:
            tarjan(v, u)
            low[u] = min(low[u], low[v])
            if low[v] > dfn[u]:
                isbridge[v] = True
                cnt_bridge = cnt_bridge + 1
        elif dfn[v] < dfn[u] and v != fa:
            low[u] = min(low[u], dfn[v])
```

Tarjan 算法还有许多用途，常用的例如求强连通分量，缩点，还有求 2-SAT 的用途等。