概率论与数理统计原理记录(期末速成版)
概率论
求分布律就是列表:数值对应相应概率。
重要符号:分布函数 \(F(x)\),概率密度 \(f(x)\)

总结:单增、有界性 \((0,1)\)、右连续性
求交并补那些的要画韦恩图辅助理解!!
方差:\(D(x)=E(x^2)-(Ex)^2\), \(D(ax+c)=a^2D(x)\)
与求积分的结合
二重积分:分段 + 复合求定积分

求 \(f(x,y)\) 的二重积分:画图求交集(交面积)。
一维连续型随机变量
对于连续型随机变量 \(X\),有 \(P\{X=x\}\leq F(x)\)
已知 \(f_x(x)\) 求概率
\(P(a<x<b)=\int_a^b f_x(x)dx\),带入具体式子求定积分。
求 \(f_x(x)\) 中的未知数
根据 \(f_{-\infty}^{+\infty}f_x(x)dx=1\) 解方程。
已知 \(f\) 求 \(F\)
\(F_A(b)\leftrightarrow P(A\leq b), F(b)\leftrightarrow P(B\leq b)\)
求 \(F\) 中的未知数
\(F(+\infty)=1, F(-\infty)=0, F(分段点^+)=F(分段点^-)\)
已知 \(F\) 求 \(f\)
\(f_A(a)=F_A'(a)\)
已知 \(f\) 求 \(f\)
先根据3. 求出 \(F\),再求导得 \(f\)
求期望
\(E[g(x)]=\int_{-\infty}^{+\infty}g(x)f_x(x)dx\)
二维连续型随机变量
求边缘密度:对另一个变量逆偏导

在转折点划分区域,分段求。


已知 \(F\) 求 \(f\)
\(F(x,y)\) 先对 \(x\) 偏导,再对 \(y\) 偏导。
求 \(F(x,y)\) 中的未知数
\(F(+\infty,+\infty)=1, F(x,-\infty)=0, F(-\infty,y)=0\)
已知 \(F(x,y)\) 求 \(F_X(x),F_Y(y)\)
\(F_X(x)=F(x,+\infty),F_Y(y)=F(+\infty,y)\),记得把相应变量的范围写在后面。
常见分布
均匀、泊松、指数、二项分布


\(\phi(x)\) 相关
正态分布
先解出 \(\mu\) 和 \(\sigma\) (一般是正的),再连同 \(a,b\) 代入右边的表格。

随机变量的数字特征、极限定理
\(E(XY)=EXEY+Cov(X,Y)=EXEY+\rho_{XY}\sqrt{DX}\sqrt{DY}\),再利用 \(D(X)=E(X^2)+E(X)^2\)
协方差 Cov
协方差:\(\sigma_{XY},cov(X,Y)\)
\(\rho_{XY}\) 已知时, \(Cov(X,Y)=\rho_{XY}\sqrt{DX}\sqrt{DY}\)
\(\rho_{XY}\) 未知时, \(Cov(X,Y)=E(XY)-EX\cdot EY\)
重要性质:
\(cov(X,X)=D(X)\)
\(cov(X,Y)=cov(Y,X), cov(aX,bY)=ab\cdot cov(X,Y),cov(X_1+X_2,Y)=cov(X_1,Y)+cov(X_2,Y)\)
相关系数 \(\rho\)
\(X,Y\) 满足 \(Y=aX+b\) 时,\(\rho_{XY}=1(a>0),\rho_{XY}=-1(a<0)\);
不满足时, \(\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{DX}\sqrt{DY}}\)
\(\rho_{XY}\in [-1,1]\)
含 \(X,Y\) 的 \(D\)
\(D(aX+bY+c)=a^2DX+b^2DY+2abCov(X,Y)\)
\(X,Y\) 相互独立
\(\leftrightarrow\) \(X,Y\) 不相关(\(\rho_{XY}=0\))
\(\leftrightarrow Cov(X,Y)=0\)
\(\leftrightarrow E(XY)=EX\cdot EY\)
\(\leftrightarrow D(X\pm Y)=DX+DY\)
切比雪夫不等式
原型:\(P\{|X-EX|\geq \epsilon\}\leq \frac{DX}{\epsilon^2}\)
大数定律
满足切比雪夫大数定律的条件:相互独立,方差一致有上界
题目出现:设随机变量 \(X_1,X_2,...,X_n\) 相互独立,且均服从参数为 \(\lambda\) 的泊松分布,

答案为:
其中,
中心极限定理
某东西均值为 \(\mu\),方差为 \(\sigma^2\)时, \(n\) 个该类东西之和为 \(X\)~\(N(n\mu,n\sigma^2)\)
从而转化为正态分布的题。
已知 \(X_1,X_2,...,X_n\) 独立同分布,期望为 \(\mu\),方差为 \(\sigma^2\),则
ADD
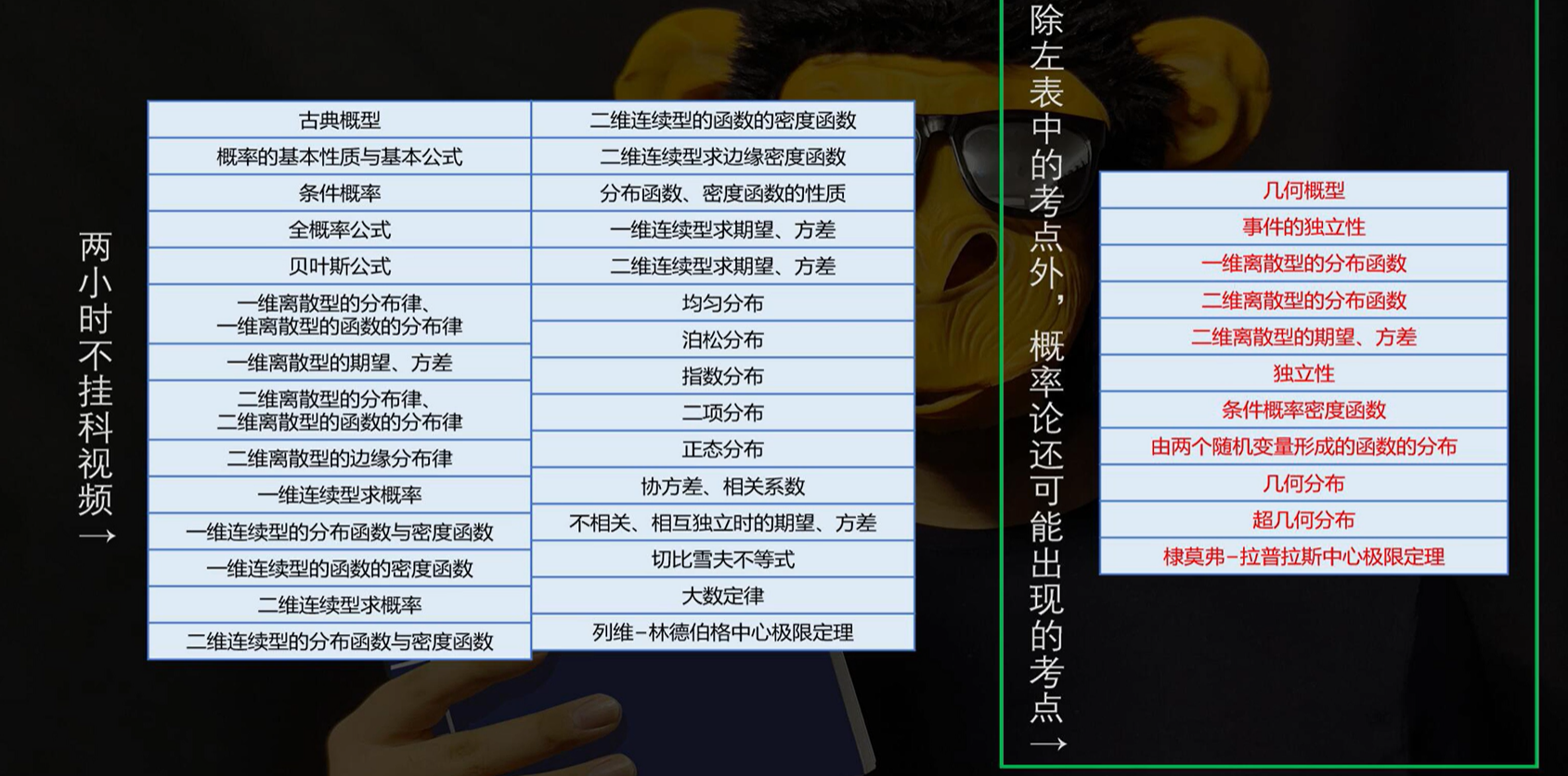
数理统计

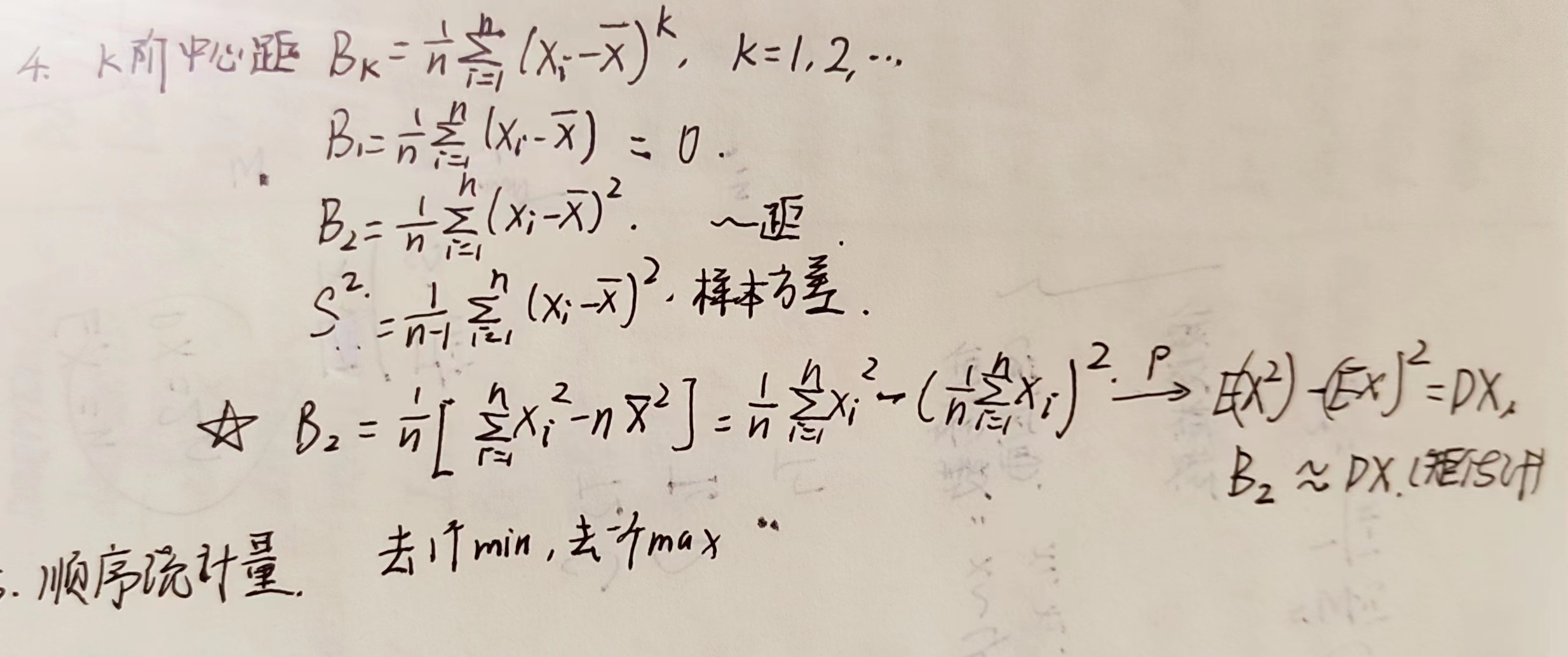
数理统计基础
求统计量的期望和方差
\(E\overline{X}=EX,E(S^2)=DX,D\overline{X}=\frac1nDX\)
服从三大分布
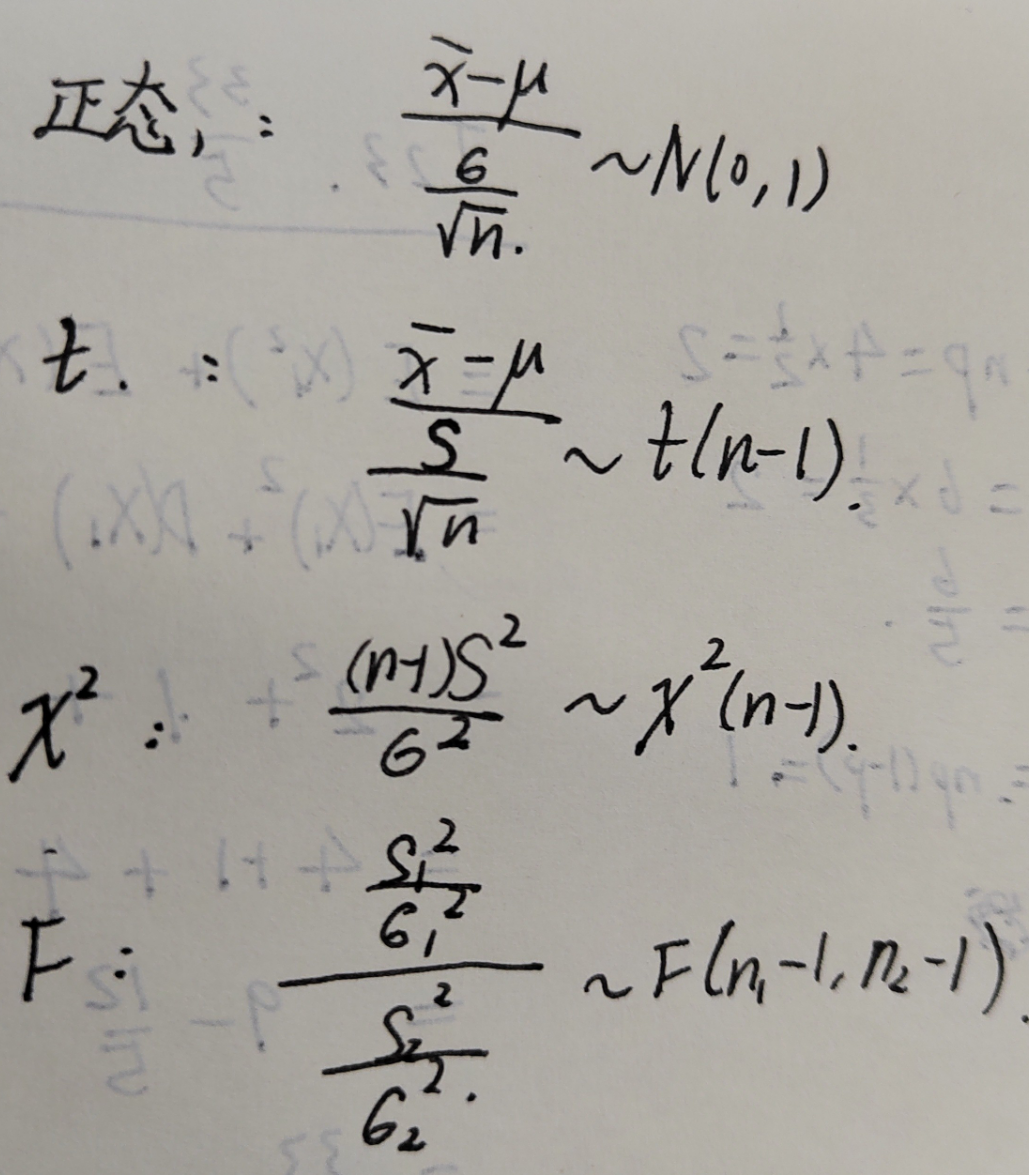

判断什么分布
某平方比某平方:F分布
一定要化成这三种形式,要不然就会扣分。

总体服从正态分布的小题

参数估计
矩估计
一阶矩估计就是期望

最大似然估计法

区间估计

表

假设检验


回归分析
线性回归

检验回归效果 是否显著

查表
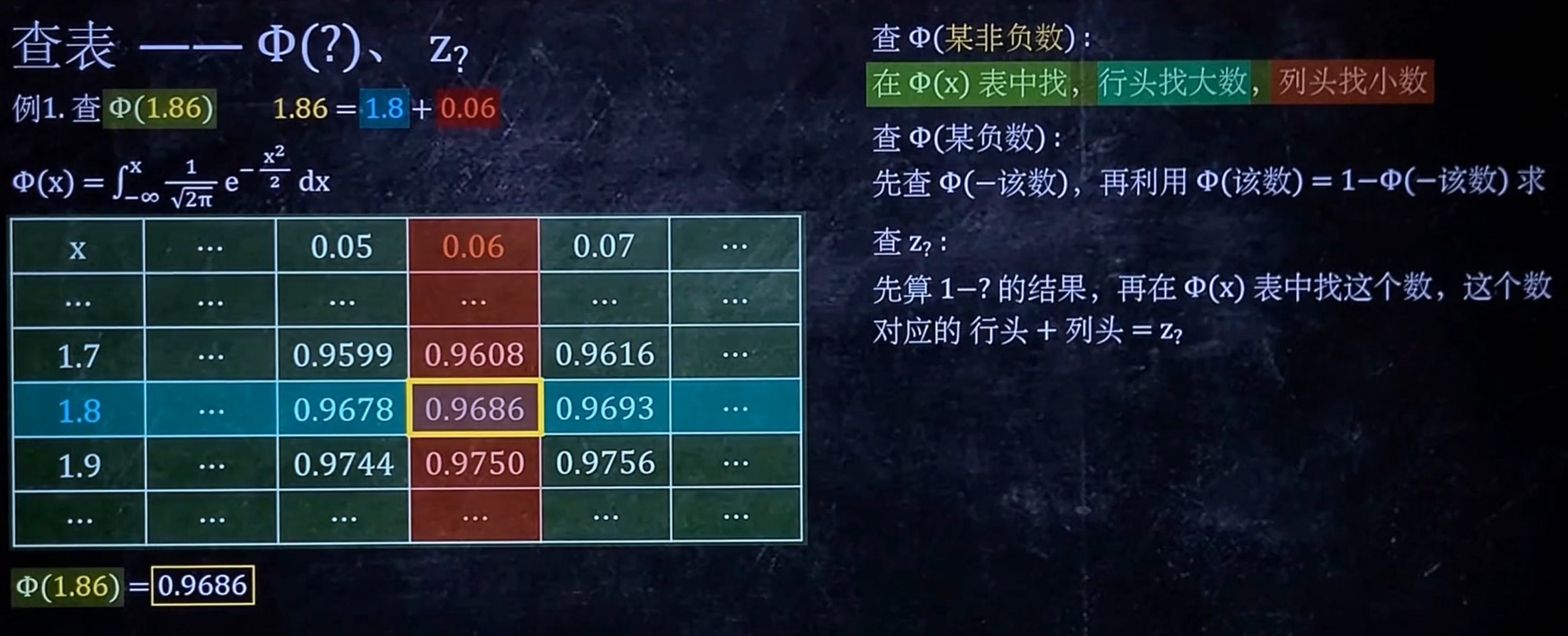
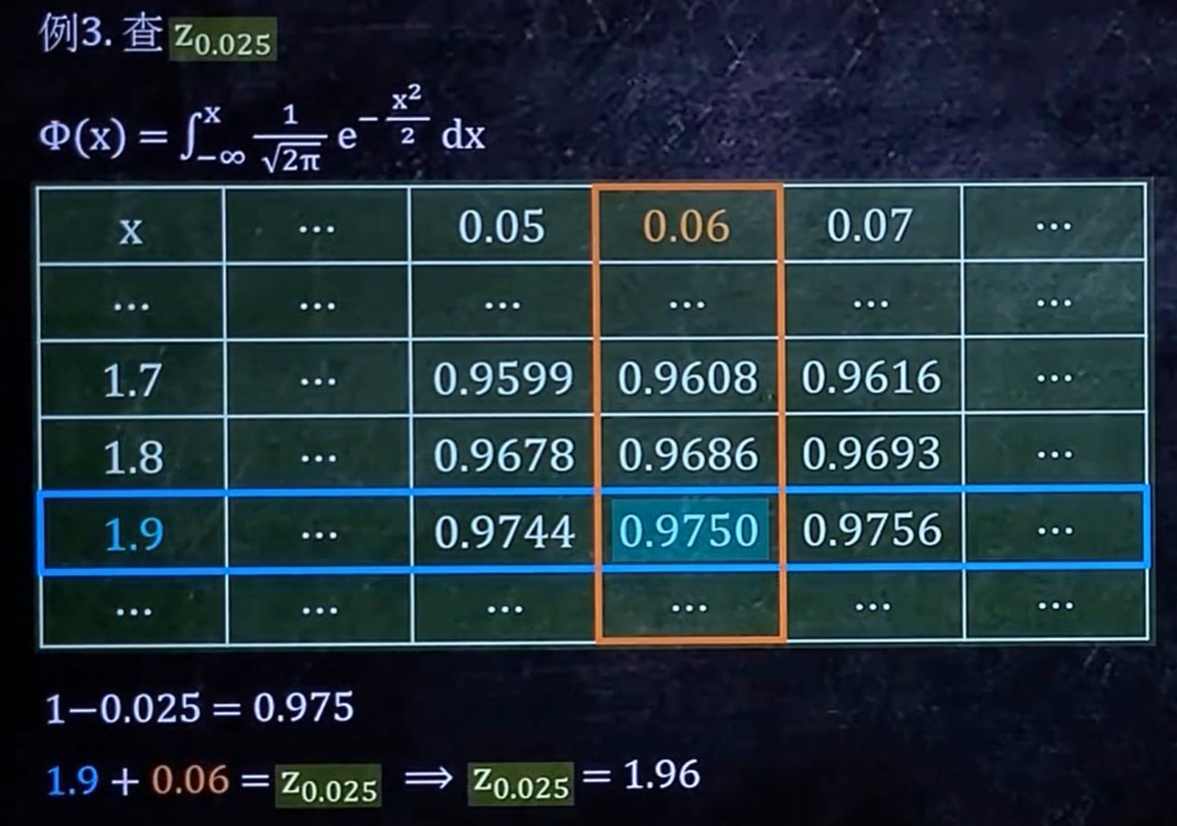
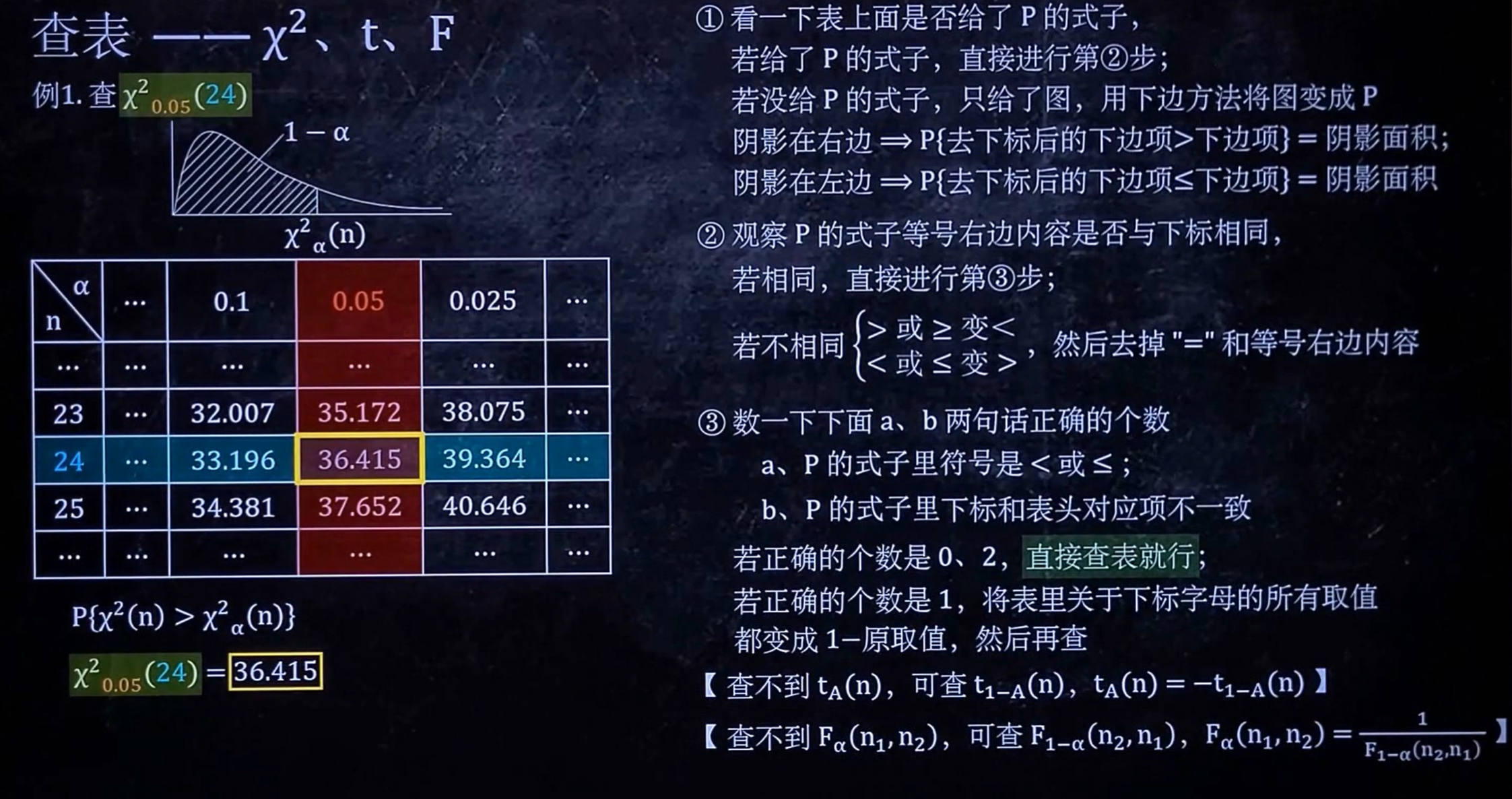
区间估计

辨析
独立与不相关
独立:没有关系 \(P(X)P(Y)=P(XY)\)
不相关:没有线性关系 \(cov=\rho=0\)
独立一定不相关,不相关不一定独立
\(A,B\) 独立不代表 \(P(AB)=0\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号