【kuangbin】专题四 最短路
【kuangbin】专题四 最短路
https://www.acwing.com/activity/content/90/
(没做的那道是网络流)

1. 青蛙
1-2最长边最短
每两点的距离都更新一下,存一个最小值连到2
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
typedef pair<double, int> pdi; //距离 编号
const int N = 205;
int n;
pii g[N];
double d[N];
double count (int a, int b) {
return sqrt ((g[a].first - g[b].first) * (g[a].first - g[b].first) + (g[a].second - g[b].second) * (g[a].second - g[b].second));
}
void test () {
for (int i = 1; i <= n; i ++)
cout << d[i] << ' ';
cout << endl;
}
void solve () {
for (int i = 1; i <= n; i ++) d[i] = 0x3f3f3f3f;
d[1] = 0;
priority_queue <pdi, vector <pdi>, greater <pdi>> q;
q.push ({0, 1});
//test ();
while (!q.empty ()) {
auto t = q.top ();
q.pop ();
double dis = t.first;
int id = t.second;
if (dis > d[id]) continue; //已是最优
//cout << "&";
for (int i = 2; i <= n; i ++) {
double cur = max (dis, count (i, id)); //当前最大距离
if (cur < d[i]) {
//cout << "&";
d[i] = cur;
q.push ({d[i], i});
}
}
}
//test ();
cout << fixed << setprecision (3) << d[2] << endl << endl;
}
//固定一点,更新距离
int main () {
int cnt = 0;
while (cin >> n, n) {
cnt ++;
cout << "Scenario #" << cnt << endl;
cout << "Frog Distance = ";
for (int i = 1; i <= n; i ++) cin >> g[i].first >> g[i].second;
if (n == 2) {
cout << fixed << setprecision (3) << count (1, 2) << endl << endl;
continue;
}
solve ();
}
}
2. 货物运输
题意:1-n最短边最最长
与1. 正好相反
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int N = 1005;
int n, m;
int e[N][N];
int dis[N];
int dijkstra () {
priority_queue <pii> q;
memset (dis, 0, sizeof dis);
dis[0] = 1e9;
q.push ({1e9, 1});
while (!q.empty ()) {
auto t = q.top ();
q.pop();
int dist = t.first, ver = t.second;
if (dis[ver] > dist) continue;
for (int i = 1; i <= n; i ++) {
int x = min (dist, e[ver][i]);
if (x > dis[i]) {
dis[i] = x;
q.push ({x, i});
}
}
}
return dis[n];
}
void solve () {
memset (e, 0, sizeof e);
cin >> n >> m;
while (m --) {
int a, b, c;
cin >> a >> b >> c;
e[a][b] = e[b][a] = c;
}
cout << dijkstra () << endl << endl;
}
int main () {
int t;
cin >> t;
for (int i = 1; i <= t; i ++) {
cout << "Scenario #" << i << ":\n";
solve ();
}
}
//与青蛙相反,求最小值最大
3. 农场派对
求 最短路径(一个来回)中最长的一条的长度
正反各一次dijkstra,把答案加起来
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 5;
int dis[N][2];
int n, m, x;
bool vis[N];
int h[N], e[N], ne[N], w[N], idx;
void add (int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dijkstra (int id) {
memset (vis, false, sizeof vis);
dis[x][id] = 0;
priority_queue <pii, vector <pii>, greater <pii>> q;
q.push ({dis[x][id], x});
while (!q.empty ()) {
auto t = q.top ();
q.pop ();
int dist = t.first, ver = t.second;
if (vis[ver]) continue;
vis[ver] = true;
for (int i = h[ver]; ~i; i = ne[i]) {
int j = e[i];
if (dis[j][id] > dist + w[i]) {
dis[j][id] = dist + w[i];
q.push ({dis[j][id], j});
}
}
}
}
int a[N], b[N], c[N];
int main () {
memset (dis, 0x3f, sizeof dis);
memset (h, -1, sizeof h);
cin >> n >> m >> x;
for (int i = 0; i < m; i ++) {
cin >> a[i] >> b[i] >> c[i];
add (a[i], b[i], c[i]);
}
dijkstra (0);
memset (h, -1, sizeof h), idx = 0;
for (int i = 0; i < m; i ++)
add (b[i], a[i], c[i]);
dijkstra (1);
int ans = 0;
for (int i = 1; i <= n; i ++)
ans = max (ans, dis[i][0] + dis[i][1]);
cout << ans << endl;
}
//最短路中最长的一条
//正反做两次dij
4. 货币兑换
类似这种,“多次辗转,回到自身,看有无增加或减少的”,容易想到spfa判正环/负环
注意一些和求负环不一样的地方
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int n, m, s;
double v;
double r[N], c[N], dis[N];
int h[N], e[N], ne[N], idx;
int cnt[N];
bool vis[N]; //是否在队列中
void add (int a, int b, double rr, double cc) {
e[idx] = b, ne[idx] = h[a], r[idx] = rr, c[idx] = cc, h[a] = idx ++;
}
bool spfa () {
queue<int> q;
q.push (s), vis[s] = true;
dis[s] = v;
// for (int i = 1; i <= n; i ++) {
// q.push (i);
// vis[i] = true;
// } //区别于求负环
while (!q.empty ()) {
auto t = q.front ();
q.pop ();
vis[t] = false;
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
double k = (dis[t] - c[i]) * r[i];
if (dis[j] < k) { //注意反向,因为是看正回路
//if (j == s) return true;
dis[j] = k;
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true;
if (!vis[j]) vis[j] = true, q.push (j);
}
}
}
return false;
}
int main () {
memset (h, -1, sizeof h);
cin >> n >> m >> s >> v;
while (m --) {
int a, b;
double r1, r2, c1, c2;
cin >> a >> b >> r1 >> c1 >> r2 >> c2;
add (a, b, r1, c1);
add (b, a, r2, c2);
}
if (spfa ()) cout << "YES\n";
else cout << "NO\n";
}
//求是否存在正权回路
//spfa判正环
5. 虫洞
“在出发时刻之前回到出发地”就是 走一圈回来,变小了,也就是存在负环,用spfa判断即可
#include <bits/stdc++.h>
using namespace std;
const int N = 505, M = 5205; //注意边的数量是5000+200
int t, n, m1, m2;
int h[N], e[M], ne[M], w[M], idx;
int dis[N], cnt[N];
bool vis[N];
void add (int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
bool spfa () {
queue <int> q;
for (int i = 1; i <= n; i ++) {
q.push (i);
vis[i] = true;
dis[i] = cnt[i] = 0;
}
while (!q.empty ()) {
int t = q.front ();
q.pop ();
vis[t] = false; //出队
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (dis[j] > dis[t] + w[i]) {
dis[j] = dis[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true;
if (!vis[j]) vis[j] = true, q.push (j); //入队
}
}
}
return false;
}
int main () {
cin >> t;
while (t --) {
memset (h, -1, sizeof h), idx = 0; //初始化要做全套啊
cin >> n >> m1 >> m2;
while (m1 --) {
int a, b, c;
cin >> a >> b >> c;
add (a, b, c), add (b, a, c);
}
while (m2 --) {
int a, b, c;
cin >> a >> b >> c;
add (a, b, -c);
}
if (spfa())
cout << "YES" << endl;
else
cout << "NO" << endl;
}
}
//时间变小了也就相当于存在负环,把值变小
//转化为spfa判断是否存在负环
6. 传递信息
读题害死人,一开始看时间叠加,就去求最小生成树了
传递是同时进行的,所以要看的是1到所有点的距离当中的最大值
也就是最长边最短
因此同1.直接跑最短路
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio (0);cin.tie(0);
using namespace std;
typedef pair <int, int> pii;
const int N = 20005;
int n, dis[N];
int h[N], e[N], ne[N], w[N], idx;
bool vis[N];
void add (int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
int to_int(string s){
int res = 0;
for(int i = 0,l = s.size();i < l; ++i) res = res * 10 + s[i] - '0';
return res;
}
void dijkstra () {
memset (dis, 0x3f, sizeof dis);
dis[1] = 0;
priority_queue <pii, vector <pii>, greater<pii>> q;
q.push ({0, 1});
while (!q.empty ()) {
auto t = q.top ();
q.pop();
int dist = t.first, ver = t.second;
if (vis[ver]) continue;
vis[ver] = true;
for (int i = h[ver]; ~i; i = ne[i]) {
int j = e[i];
if (dis[j] > dist + w[i]) {
dis[j] = dist + w[i];
q.push ({dis[j], j});
}
}
}
}
int main () {
IOS;
memset (h, -1, sizeof h);
cin >> n;
for (int i = 2; i <= n; i ++)
for (int j = 1; j < i; j ++) {
string s;
cin >> s;
if (s != "x") {
int x = to_int(s);
add (i, j, x);
add (j, i, x);
}
}
dijkstra ();
int ans = 0;
for (int i = 2; i <= n; i ++) ans = max (ans, dis[i]);
cout << ans << endl;
}
//以1为源点的最小生成树
//烦死了。。读错题了,不是最小生成树
//传递是同时进行的,所以要看的是1到所有点的距离当中的最大值
//直接跑dijkstra
7. 牛的比赛
看看N,只有100,考虑floyd(主要是因为要确定n-1条边的关系)
如果能和其他n-1个节点建立直接或间接的关系,那么排名就能确定了
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int N = 105;
int n, m;
int f[N][N];
int main () {
cin >> n >> m;
while (m --) {
int a, b;
cin >> a >> b;
f[b][a] = 1;
}
//test ();
for (int k = 1; k <= n; k ++)
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= n; j ++)
f[i][j] |= (f[i][k] && f[k][j]); //直接有值或间接更新得到
int ans = 0;
for (int i = 1; i <= n; i ++) {
int cnt = 0;
for (int j = 1; j <= n; j ++)
if (f[i][j] | f[j][i]) cnt ++;
if (cnt == n - 1) ans ++; //和我分析的一致
}
cout << ans << endl;
}
//度为n-1的节点一定能确定
//再根据已经确定的推未知的
//迭代更新的思想还是挺像最短路的
8. 最短路径和
题目已经说得十分清楚,就是粗暴地把所有最短路加起来
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e6 + 5;
int h[N], hh[N], e[N<<1], ne[N<<1], w[N<<1], idx;
int dis1[N], dis2[N], n, m;
bool vis[N];
void add (int a, int b, int c, int *h) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dijkstra (int *h, int *dis) {
memset (dis, 0x3f, sizeof dis);
memset (vis, false, sizeof vis);
dis[1] = 0;
priority_queue <pii, vector <pii>, greater <pii>>q;
q.push ({0, 1});
while (!q.empty ()) {
auto t = q.top();
q.pop();
int ver = t.second, dist = t.first;
if (vis[ver]) continue;
vis[ver] = true;
for (int i = h[ver]; ~i; i = ne[i]) {
int j = e[i];
if (dis[j] > dist + w[i]) {
dis[j] = dist + w[i];
q.push ({dis[j], j});
}
}
}
}
void solve () {
memset (h, -1, sizeof h);
memset (hh, -1, sizeof hh);
//记得dis要初始化
memset (dis1, 0x3f, sizeof dis1);
memset (dis2, 0x3f, sizeof dis2);
cin >> n >> m;
while (m --) {
int a, b, c;
cin >> a >> b >> c;
add (a, b, c, h);
add (b, a, c, hh);
}
dijkstra (h, dis1);
dijkstra (hh, dis2);
long long ans = 0;
for (int i = 1; i <= n; i ++)
ans += dis1[i] + dis2[i];
cout << ans << endl;
}
int main () {
int t;
cin >> t;
while (t --) {
solve ();
}
}
//正反两次dijkstra
9. 糖果
将 “a 认为小朋友 b 的糖果数量最多只可以比他多 c 个” 抽象为a到b的最大边权,然后依次建边即可
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int N = 30005, M = 150005;
int n, m;
int h[M], e[M], ne[M], w[M], idx;
int dis[N];
bool vis[N];
void add (int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
int dijkstra () {
//memset (dis, 0x3f, sizeof dis);
memset (vis, false, sizeof vis);
dis[1] = 0;
priority_queue <pii, vector<pii>, greater <pii>>q;
q.push ({0, 1});
while (!q.empty ()) {
auto t = q.top ();
q.pop();
int ver = t.second, dist = t.first;
if (vis[ver]) continue;
vis[ver] = true;
for (int i = h[ver]; ~i; i = ne[i]) {
int j = e[i];
if (dis[j] > dist + w[i]) {
dis[j] = dist + w[i];
q.push ({dis[j], j});
}
}
}
return dis[n];
}
int main () {
cin >> n >> m;
memset (h, -1, sizeof h);
while (m --) {
int a, b, c;
cin >> a >> b >> c;
add (a, b, c);
}
cout << dijkstra () << endl;
}
// n 最多比小朋友 1 多分到的糖果数量的最大可能
//dijkstra板子
10. 地铁
取两种方式中更快的来更新距离
然后看数据范围:200个点
floyd得到最优方案
别忘了单位转换
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int N = 205;
double dis[N][N];
int n;
vector <pii> v(2);
double dist (int i, int j) {
return sqrt ((v[i].first - v[j].first) *(v[i].first - v[j].first) + (v[i].second - v[j].second) *(v[i].second - v[j].second)) * 0.006;
//km/h -> m/min
}
int main () {
for (int i = 0; i < N; i ++)
for (int j = 0; j < N; j ++) {
if (i == j) dis[i][j] = 0;
else dis[i][j] = 0x3f3f3f3f;
}
cin >> v[0].first >> v[0].second >> v[1].first >> v[1].second;
int x, y, cnt = 2;
while (cin >> x >> y) {
//纯坐地铁的路径更新
if (x == -1 && y == -1) {
for (int i = cnt; i < v.size (); i ++)
for (int j = i + 1; j < v.size (); j ++)
dis[j][i] = dis[i][j] = dis[i][j-1] + dist (j, j-1) / 4;
cnt = v.size(); //下一条路线的起点
}
else v.push_back ({x, y});
}
n = v.size ();
for (int i = 0; i < n; i ++)
for (int j = 0; j < n; j ++)
dis[i][j] = min (dis[i][j], dist (i, j)); //坐地铁or走路
//floyd
for (int k = 0; k < n; k ++)
for (int i = 0; i < n; i ++)
for (int j = 0; j < n; j ++)
dis[i][j] = min (dis[i][j], dis[i][k] + dis[k][j]);
cout << (int) (dis[0][1] + 0.50) << endl;
}
//n只有200,可以floyd
11. 昂贵的聘礼
就是要通过不同的物品迭代更新
从不同的人那里选择性进行物品替代
建图:增加一个虚拟源点0
所以这个就是有范围限制的最短路,枚举等级范围,再更新最小值
放一个y总的图辅助理解
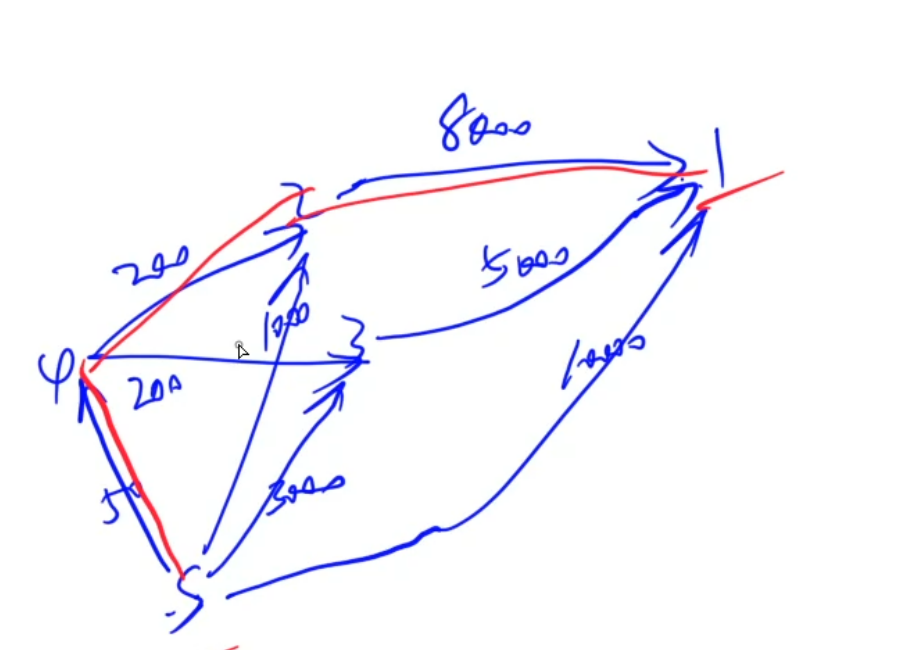
#include <bits/stdc++.h>
using namespace std;
const int N = 105;
int n, m;
bool vis[N];
int dis[N], a[N][N], level[N];
int dijkstra (int st, int ed) {
memset (dis, 0x3f, sizeof dis);
memset (vis, false, sizeof vis);
dis[0] = 0;
//普通dijkstra
for (int i = 1; i <= n; i ++) {
int t = -1;
for (int j = 0; j <= n; j ++) { //从0开始!!虚拟源点
if (!vis[j] && (t == -1 || dis[t] > dis[j]))
t = j;
}
vis[t] = true;
for (int j = 1; j <= n; j ++)
if (level[j] >= st && level[j] <= ed)
dis[j] = min (dis[j], dis[t] + a[t][j]);
}
return dis[1];
}
int main () {
memset (a, 0x3f, sizeof a);
cin >> m >> n;
for (int i = 1; i <= n; i ++)
a[i][i] = 0;
for (int i = 1; i <= n; i ++) {
int p, x;
cin >> p >> level[i] >> x;
a[0][i] = min (p, a[0][i]);
while (x --) {
int t, v;
cin >> t >> v;
a[t][i] = min (a[t][i], v);
}
}
int ans = 0x7fffffff;
for (int i = level[1] - m; i <= level[1]; i ++) //从酋长开始交易的
ans = min (ans, dijkstra(i, i + m));
cout << ans << endl;
}
12. 电车
不需要变向就边权为0, 否则为1
然后dijkstra
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int N = 2e4 + 5;
int n, st, ed;
int h[N], e[N], ne[N], w[N], idx;
bool vis[N];
int dis[N];
void add (int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
int dijkstra () {
memset (dis, 0x3f, sizeof dis);
memset (vis, false, sizeof vis);
dis[st] = 0;
priority_queue <pii, vector <pii>, greater <pii>> q;
q.push ({0, st});
while (!q.empty ()) {
auto t = q.top ();
q.pop();
int ver = t.second, dist = t.first;
if (vis[ver]) continue;
vis[ver] = true;
for (int i = h[ver]; ~i; i = ne[i]) {
int j = e[i];
if (dis[j] > dist + w[i]) {
dis[j] = dist + w[i];
q.push ({dis[j], j});
}
}
}
if (dis[ed] == 0x3f3f3f3f) return -1;
return dis[ed];
}
int main () {
memset (h, -1, sizeof h);
cin >> n >> st >> ed;
for (int i = 1; i <= n; i ++) {
int m; cin >> m;
for (int j = 0; j < m; j ++) {
int x; cin >> x;
if (j == 0) add (i, x, 0);
else add (i, x, 1);
}
}
cout << dijkstra () << endl;
}
//最短路
//建边,i到d[1]的权值为0
13. Nya图最短路
看到建立虚拟源点的做法,学习一下
核心:建边

堆优化dijkstra也可以过,就是建边的方式和SPFA不同
spfa:
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int N = 2e5 + 5, M = N << 2;
int h[N], e[M], ne[M], w[M], idx;
int dis[N];
bool vis[N];
int n, m, c;
void add (int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
int spfa () {
memset (vis, false, sizeof vis);
memset (dis, 0x3f, sizeof dis);
dis[1] = 0, vis[1] = true;
queue <int> q;
q.push (1);
while (!q.empty ()) {
auto t = q.front ();
q.pop();
vis[t] = false;
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (dis[j] > dis[t] + w[i]) {
dis[j] = dis[t] + w[i];
if (!vis[j]) q.push (j), vis[j] = true;
}
}
}
if (dis[n] == 0x3f3f3f3f) return -1;
return dis[n];
}
int main () {
int t;
cin >> t;
for (int _ = 1; _ <= t; _ ++) {
cout<<"Case #"<<_<<": ";
cin >> n >> m >> c;
memset (h, -1, sizeof h), idx = 0;
for (int i = 1; i <= n; i ++) {
int x; cin >> x;
//更新阶梯
add (x + n, i, 0);
if (x < n) add (i, x + n + 1, c);
if (x > 1) add (i, x + n - 1, c);
}
while (m --) {
//更新额外边
int a, b, c;
cin >> a >> b >> c;
add (a, b, c), add (b, a, c);
}
cout << spfa () << endl;
}
}
堆优化dijkstra:
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int N = 2e5 + 5, M = N << 2;
int h[N], e[M], ne[M], w[M], idx;
int dis[N];
bool vis[N];
int n, m, c;
void add (int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
int dijkstra () {
memset (vis, false, sizeof vis);
memset (dis, 0x3f, sizeof dis);
dis[1] = 0;
priority_queue <pii, vector <pii>, greater <pii>> q;
q.push ({0, 1});
while (!q.empty ()) {
auto t = q.top();
q.pop();
int ver = t.second, dist = t.first;
if (vis[ver]) continue;
vis[ver] = true;
for (int i = h[ver]; ~i; i = ne[i]) {
int j = e[i];
if (dis[j] > dist + w[i]) {
dis[j] = dist + w[i];
q.push ({dis[j], j});
}
}
}
if (dis[n] == 0x3f3f3f3f) return -1;
return dis[n];
}
int main () {
int t;
cin >> t;
for (int _ = 1; _ <= t; _ ++) {
cout<<"Case #"<<_<<": ";
cin >> n >> m >> c;
memset (h, -1, sizeof h), idx = 0;
for (int i = 1; i <= n; i ++) {
int x; cin >> x;
//更新阶梯
add (x + n, i, 0);
if (x < n) add (i, x + n + 1, c);
if (x > 1) add (i, x + n - 1, c);
}
while (m --) {
//更新额外边
int a, b, c;
cin >> a >> b >> c;
add (a, b, c), add (b, a, c);
}
cout << dijkstra () << endl;
}
}
14. 规划最短路
网络流,pass
15. 0或1
(看成邻接矩阵存图)
- 是说1只有一个出度
- n只有一个入度
- 2~n-1之间,每一个数的出入度都相等
关键在于抽象题意
ans(取min):
1出发的一个环和从n出发的环之和
1-n之间的最短路
#include <bits/stdc++.h>
using namespace std;
const int N = 305;
int a[N][N], dis[N];
bool vis[N];
int n;
void spfa (int x) {
queue <int> q;
for (int i =1; i <= n; i ++)
dis[i] = a[x][i], vis[i] = true, q.push (i);
dis[x] = 0x3f3f3f3f, vis[x] = false; //环,先把自己放飞,再通过后续更新回来
while (!q.empty ()) {
auto t = q.front ();
q.pop ();
vis[t] = false;
for (int i = 1; i <= n; i ++) {
if (dis[i] > dis[t] + a[t][i]) {
dis[i] = dis[t] + a[t][i];
if (!vis[i]) vis[i] = true, q.push (i);
}
}
}
}
int main () {
while (cin >> n) {
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= n; j ++)
cin >> a[i][j];
spfa (1);
int d1 = dis[1], d2 = dis[n]; //1环,1-n之间的最短路
spfa (n);
int d3 = dis[n];
cout << min (d1 + d3, d2) << endl;
}
}
// 1. 是说1只有一个出度
// 2. n只有一个入度
// 3. 2~n-1之间,每一个数的出入度都相等
//关键在于抽象题意
//ans(取min):
//1出发的一个环和从n出发的环之和
//1-n之间的最短路
16. 排队布局
最大值,最短路问题
限制条件:\(x_b-x_a\leq L\) 和 \(x_b-x_a\geq D\)
- \(x_{i}\leq x_{i+1}, \,\, 1\leq i < b\)
- \(x_b\leq x_a+L\)
- \(x_a\leq x_b-D\)
#include <bits/stdc++.h>
using namespace std;
const int N = 1005, M = N + 2e4;
int n, L, D;
int dis[N], cnt[N];
bool vis[N];
int h[N], e[M], ne[M], w[M], idx;
void add (int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
bool spfa (int x) {
queue <int> q;
memset (dis, 0x3f, sizeof dis);
memset (cnt, 0, sizeof cnt);
memset (vis, false, sizeof vis);
for (int i = 1; i <= x; i ++) //x
q.push (i), vis[i] = true, dis[i] = 0;
while (!q.empty()) {
int t = q.front();
q.pop();
vis[t] = false;
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (dis[j] > dis[t] +w[i]) {
dis[j] = dis[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n)
return false;
if (!vis[j])
q.push (j), vis[j] = true;
}
}
}
return true;
}
int main () {
memset (h, -1, sizeof h);
cin >> n >> L >> D;
for (int i = 1; i < n; i ++)
add (i + 1, i, 0);
while (L --) {
int a, b, c;
cin >> a >> b >> c;
if (a > b)
swap (a, b);
add (a, b, c); //注意最短路的符号是相反的
}
while (D --) {
int a, b, c;
cin >> a >> b >> c;
if (a > b)
swap (a, b);
add (b, a, -c);
}
if (!spfa(n))
puts("-1");
else {
spfa(1);
if (dis[n] == 0x3f3f3f3f )
puts("-2");
else
cout << dis[n] << endl;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号