【线性代数】笔记 期末复习
线性代数
一、行列式
是一个数(只看结果) 且 行数等于列数
规范:行 r ,列 c
简化计算:把主对角线下方全变成0
1. 排序与逆序数
逆序数:逆序对的数量
求:看前面有几个比它大的
2. n阶行列式定义
计算:不同行不同列乘积的代数和(项数\(n!\))
先把行进行顺排列,**系数 = \((-1)^{\tau 列}\) ** ($\tau $列表示列的逆序数量)
例题1:
分析:常数项,所以不取0也不取x,然后按照每行每列只取一个的规则进行枚举,排除不可能的情况,剩下的就是所求
答案:A
例题2:
思路同上,枚举排除
答案:-5 (做对了,开心)
特殊性质:
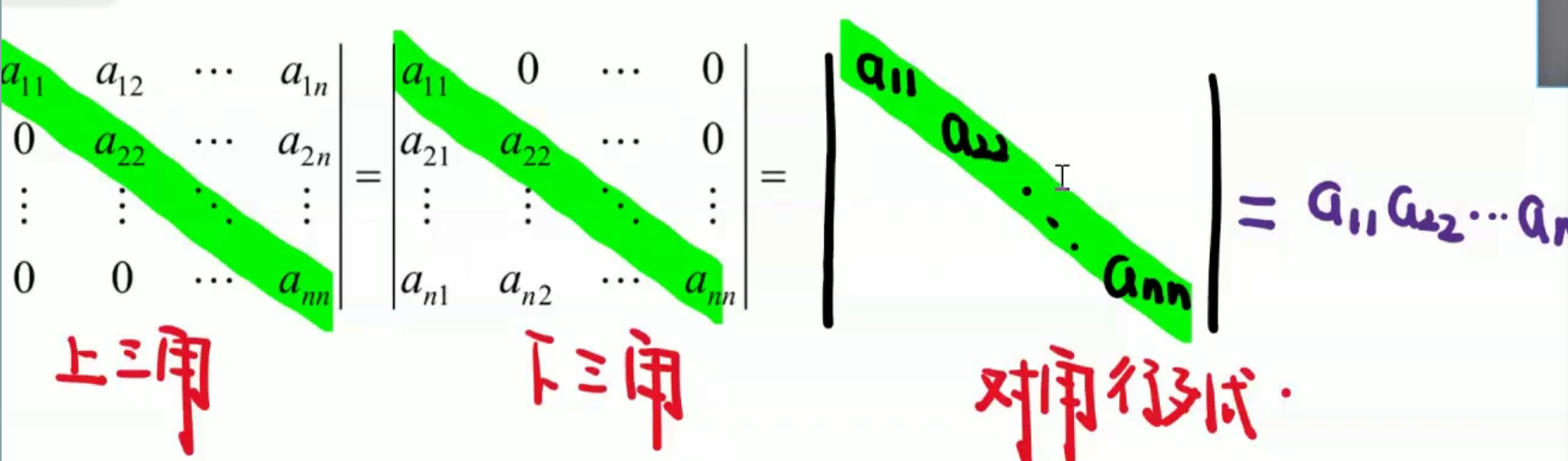
上三角、下三角、对角行列式中,值为:
- (主对角线):\(a_{11}a_{22}...a_{nn}\)
- (副对角线):\((-1)^{\frac{n(n-1)}{2}}\,a_{11}a_{22}...a_{nn}\)
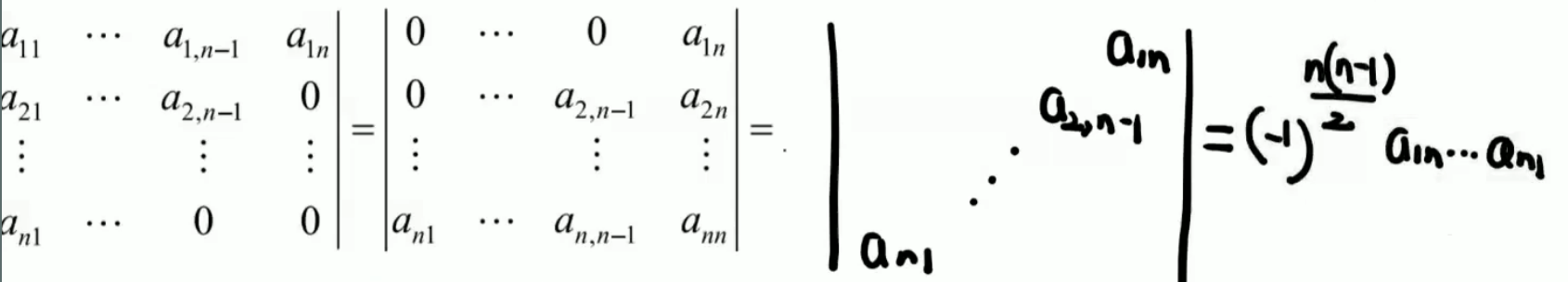
3. 性质
-
转置:经转置(i, j 互换)行列式不变
-
互换:互换两行(列),行列式变号 (推论1:如果行列式中有两行 / 列相等,那么这个行列式为0)
某行(列)乘 k ,等于 k 乘此行列式(推论2:如果行列式中有两行 / 列成比例,那么这个行列式为0)
-
倍加:某行(列)加 / 减另一行(列)的几倍,行列式不变
-
纯数值型行列式:高斯消元法(把第一列中最简单的放到第一行,下面全部变成0)
-
拆分:若行列式的某一行 / 列的元素都是两数之和,则此行列式等于两个行列式之和(只有一行 / 列不同,只能是单行单列拆分!!!)
例题:

分析:此题拆分后可以大大简化计算
答案:12
4. 展开
-
余子式\(M_{ij}\)(消去 i 行 j 列之后的结果)
-
代数余子式 \(A_{ij} = (-1)^{i + j}·M_{ij}\)
-
展开定理:该行元素和该行元素所对应的代数余子式的线性和
适用:0 比较多

某行或某列的代数余子式线性和问题:
把该行 / 列换成所求系数,所求就是行列式的值
原理:该行代数余子式的值与该行无关
若所求为余子式之和,先转化为代数余子式,再求
例题:
技巧:进行一些行列之间的加减,使得该行系数化繁为简(首项化为1)
- 展开定理性质:某一行 / 列的元素与另一行 / 列的对应元素的代数余子式乘积之和等于0
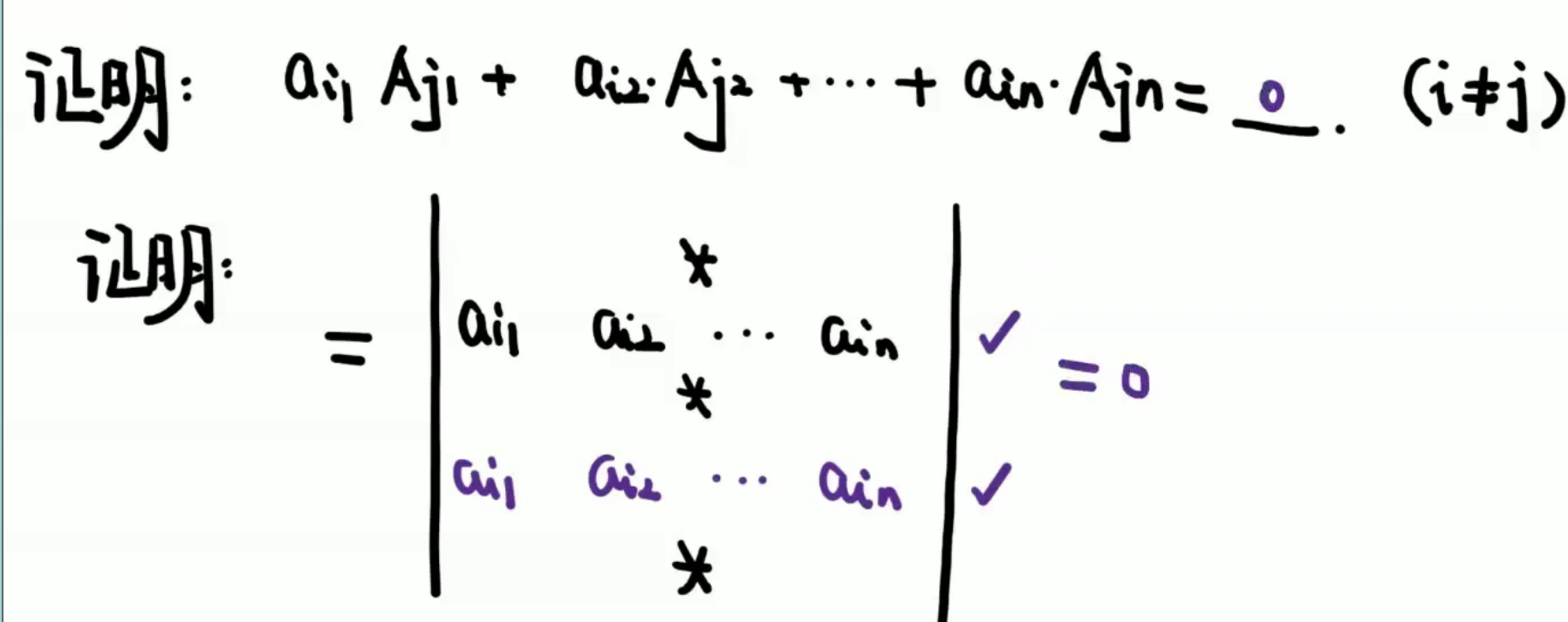
例题:
思路:化为相应系数
答案:1(第一行换成1的上三角)
5. 范德蒙行列式
例1:
例2:
典中典:
6. 计算及应用
-
\[\begin{vmatrix} x & a & ... & a\\ a & x & ... & a\\ \vdots & \vdots & \ddots & \vdots \\ a & a & ... & x \end{vmatrix} = (x - a)^{n - 1}[x + (n - 1)a] \]
对角线上是一个数,其余全一样
-
\[\begin{vmatrix} 1 & 1 & ... & 1\\ x_1 & x_2 & ... & x_n\\ x_1^2 & x_2^2 & ... & x_n^2\\ \vdots & \vdots & \ddots & \vdots \\ x_1^{n - 1} & x_2^{n - 1} & ... & x_n^{n - 1} \end{vmatrix} = (x_n - x_{n - 1})(x_n - x_{n - 2})(x_n - x_{n - 3})......(x_n - x_1)(x_{n - 1} - x_{n - 2})(x_{n - 1} - x_{n - 3})......(x_{n - 1} - x_1)......(x_2 - x_1) \]
-
- 两行 (列) 相同或成比例时, 行列式为0;
- 某行 (列) 为两项相加减时,行列式可拆成两个行列式相加减
-
求余子式\(M_{ij}\)(消去 i 行 j 列之后的结果)、代数余子式 \(A_{ij} = (-1)^{i + j}·M_{ij}\)
-
某一行或某一列只有一个非零
- 多个 A 或 M 相加减:用 A 前面的系数来替换下标所指的数,如果是 M 的话就先把它转换成 A(变符号)
- 判断方程组解的情况
(齐次:右边全0 ; 非齐次:右端有常数项存在)
7. 题型
-
行之和或列之和相等时,行相等加到第一列,列相等加到第一行,提取公因子,转化为
\[\begin{vmatrix} x & a & ... & a\\ a & x & ... & a\\ \vdots & \vdots & \ddots & \vdots \\ a & a & ... & x \end{vmatrix} = (x - a)^{n - 1}[x + (n - 1)a] \]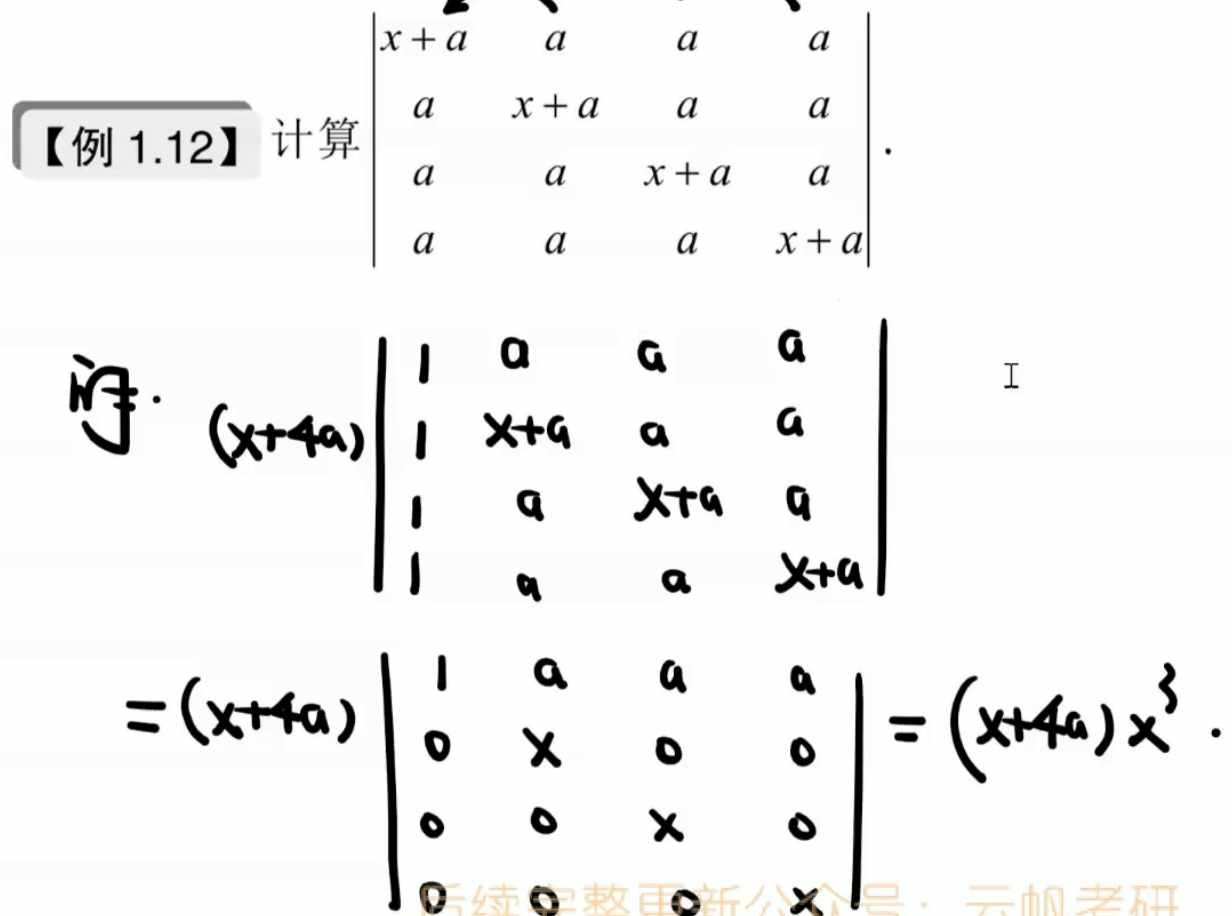
2. 矩阵
1. 矩阵相乘
前行乘后列(第 i 行第 j 列的值是第 i 行乘第 j 列的值)
特殊矩阵
- 0 矩阵 (全0)乘任何矩阵相乘都为 0 :A · 0 = 0
- 对角线为 1 ,其他都为 0 的矩阵 E 等价为 1: A · E = A
- 矩阵相乘顺序不能颠倒:\(AB \neq BA\)
- \(AX = AY\)不能推出\(X = Y\)
- \((AB)^k\) 不一定等于 \(A^kB^k\)
- \(A^2 + (k + j)AB + kjB^2\) 不一定等于 \((A + kB)(A + jB)\)
但里面有一个是 E 时,可以转化:
\(A^2 + 2A + E = A^2 + 2AE + E^2 = (A + E)^2\)
2. 矩阵取行列式
换成行列式,行列式的值就是所求
性质:\(|λA| = λ^n|A|\)
3. 矩阵转置
把第 i 行变成第 i 列
- 列乘行乘列:先用行乘列
- \((AB)^T = B^TA^T\)
- \(|A^T| = |A|\)
4. 证明矩阵可逆
- 矩阵 A 为方阵
- \(|A| \neq 0\) 或者 \(\exists B\) ,满足\(AB = E 或 BA = E\)
(两个都要满足)
5. 求逆矩阵
\((A \vdots E)\) 经过下列3个操作后变成\((E \vdots A^{-1})\)
- 换行
- 某行乘上一个数字
- 一行加上或减去另一方乘数字
(也就是把 A 变成 1 矩阵,右边 E 所进行相应变换的结果就是所求)
6. 利用 A· A-1 = E 或 A-1· A = E计算
7. 利用 A· A* = |A|E 或 A*· A = |A|E计算
直接代公式,把 \(A^*\) 消掉
8. 求矩阵的秩
进行行变换,使得下行左端 0 比上行多,直到下面行全为 0 为止(化为“严格阶梯型“)
化完之后,非 0 行有多少个,秩就是多少
9. 已知秩,求矩阵里的未知数
先做变换,把除未知数外的尽可能化为 0
矩阵初识
方阵
下标只有一个的时候表示方阵(行数等于列数)
方阵才有主对角线
(小心i == j处的边界判断)
- 上三角形矩阵:下为0
- 下三角形矩阵:上为0
- 对角矩阵:上下都为0
表示方法:
- 数量/纯量矩阵:主对角线上的元素都相同
- 单位矩阵:主对角线上的元素都为1,用I,E来表示
线性方程
给出线性方程组可得,
先处理线性方程组:同种下标对其,没有的补0,常数项都在右边
系数矩阵:A
增广矩阵:B (带右边的常数项)
齐次方程组:常数项全为0
矩阵的初等行变换
高斯消元
解方程
高斯消元:线代行列变换——>系数矩阵(正)
初等行列变换:
- 把某一行乘一个非零的数
- 交换某两行
- 把某行的若干倍加到另一行去
经上述操作,最终解不变,方程组变为上三角形式。
解的可能性:(看三角形)
- 无解:零 = 非零
- 无穷解:零 = 零
- 唯一解:完美阶梯形
高斯消元法:
枚举每一列c(从第一列开始挨个往后看)“大顶10”
-
找绝对值最大的一行
-
将该行换到最上面
-
将该行第一个数变成1(同时除一个非零常数)
-
将下面所有行的第c列消成0(同时加减)
-
把处理完的那些列固定,重复执行1~5的操作
-
记得倒着把方程消一遍
简图:
实现过程中要小心的易错点:
- eps 辅助浮点数判断,精度问题
- 记得 “ 倒消 ” ;
- 排除-0.00的状况
- 个人犯的sb错误:赋值写成相等orz
行阶阶梯形矩阵
非0行的非0首元下面和之前的元素都是0
如果有-行,0行排在最后面
行阶最简型矩阵
非0行的非0首元都是1,上下都是0
讨论解的可能性
矩阵乘法
法则
满足以下条件之一就可以交换:
- 单位矩阵乘
- 两个对角矩阵相乘
矩阵转置
性质:
3. 向量
(1)向量空间和子空间
(2)线性组合和线性表出
(3) 线性相关 线性无关
1. 定义
存在一组不全为0的\(k\),使得:
则\(\alpha_1,\alpha_2,...,\alpha_m\)是线性相关的;
若\(k\)全为0时,等式才成立,则称\(\alpha_1,\alpha_2,...,\alpha_m\)是线性无关的;
2. 性质
-
向量组\(\alpha_1,\alpha_2,...,\alpha_m\)线性相关的充分必要条件是此向量组中至少有一个向量是其余向量的组合
-
有\(\alpha_1,\alpha_2,...,\alpha_m\)和\(\beta_1,\beta_2,...,\beta_s\)两组向量,如果二者中的每一个都可以用另一组表示出,则称两向量组等价
- “若多的可以被少的线性表示,则多的线性相关”:\(\alpha_1,\alpha_2,...,\alpha_m\)可由\(\beta_1,\beta_2,...,\beta_s\)线性表示出,且\(m>s\),则\(\alpha_1,\alpha_2,...,\alpha_m\)线性相关 (逆否亦成立)
- 两个线性无关的向量组如果等价 \(\leftrightarrow\) 所含向量个数相等
- 向量个数多于\(n\)个的\(n\)维向量组线性相关
-
“原无关,添加后仍无关;原相关,去掉后仍相关”:一组线性无关的\(n\)维向量添加\(k\)个同序号分量后得到的\(n+k\)维向量组仍然线性无关 (后略)
(4)向量空间的基和维数
1. 基
定义:向量空间\(V\)中的一组向量\(\alpha_1,\alpha_2,...,\alpha_n\)若满足 线性无关 且 \(V\)中任一向量可由此向量组线性表示出,则称该组向量为\(V\)中的一个基(基底)。
定理:若\(\alpha_1,\alpha_2,....,\alpha_s\)和\(\beta_1,\beta_2,...,\beta_t\)均为向量空间 \(W\)的基,那么必有\(s=t\)(等价)
2. 维数
定义:一向量空间\(V\not=\{O\}\)时,\(V\)的任一基所含向量个数称为\(V\)的维数;当\(V=\{O\}\)时,\(V\)的维数为0
故,\(R^n\)的维数为\(n\),即\(R^n\)为一个\(n\)维的向量空间
(5)极大无关组和向量组的秩
极大无关组:
\(\alpha_1,\alpha_2,...,\alpha_m\)的部分向量组\(\alpha_{i_1},\alpha_{i_2},...,\alpha_{i_r}\)满足 \(\alpha_{i_1},\alpha_{i_2},...,\alpha_{i_r}\)线性无关 且 向量组中的每一个\(\alpha_j\)都可以用\(\alpha_{i_1},\alpha_{i_2},...,\alpha_{i_r}\)表示出,则称\(\alpha_{i_1},\alpha_{i_2},...,\alpha_{i_r}\)为极大无关组。
性质:
- 向量组中任意两个极大无关组所含向量个数相等
- 秩:极大无关组所含的向量个数
\(\alpha_{i_1},\alpha_{i_2},...,\alpha_{i_r}\)是\(\alpha_1,\alpha_2,...,\alpha_m\)的一个极大无关组,则\(\alpha_{i_1},\alpha_{i_2},...,\alpha_{i_r}\)是向量空间\(Span(\alpha_1,\alpha_2,...,\alpha_m)\)的一个基
(6)矩阵的秩
先空着

 线性代数
线性代数




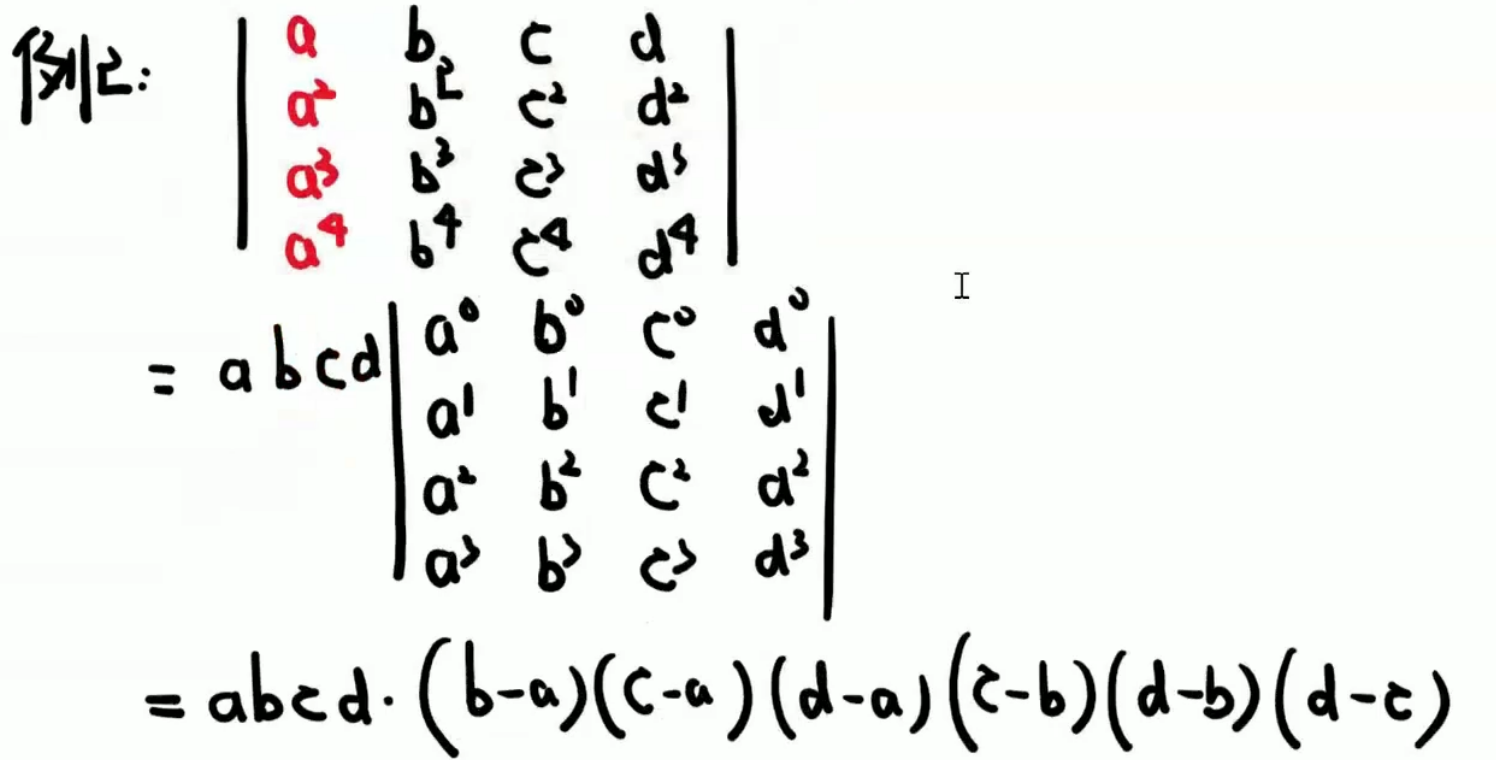



 浙公网安备 33010602011771号
浙公网安备 33010602011771号