HDU 5382 莫比乌斯反演

 题目大意：

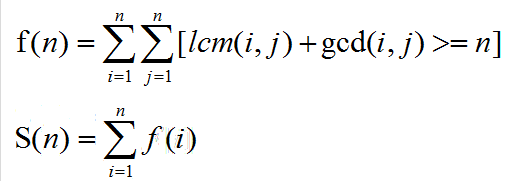
求S(n)的值 n<=1000000

 

 

 

这是官方题解给出的推导过程，orz，按这上面说的来写，就不难了

这里需要思考的就是G(n)这个如何利用积性函数的性质线性筛出来

作为一个质数，那么肯定G(i) = 2

1. 那么一个数 i 乘上了一个未出现的素数prime，那么就相当于，在当前符合的因子上面都乘了prime之后依旧符合，而原来 i 对应的数也符合，那么说明翻了两倍

也就是 g(i*prime) = 2*g(i) = g(prime) * g(i)

2. 如果这个乘上的素数prime已经存在于 i 中 ， 那么仔细想一下，只有 i 那些符合的因子中已经带prime的必须再乘上这个prime，不然这个prime跑到 i/d中，gcd = prime了，其他的都不变，说明其实 g(i*prime) = g(i) 的

#include <bits/stdc++.h>

using namespace std;
#define N 1000000
#define ll long long
const int MOD=258280327;

ll g[N+5] , t[N+5] , f[N+5];
ll sum[N+5];
int prime[N/5] , tot;
bool check[N+5];

void get_g()
{
    g[1] = 1;
    for(int i=2 ; i<=N ; i++){
        if(!check[i]) prime[tot++] = i , g[i] = 2;
        for(int j=0 ; j<tot ; j++){
            if((ll)prime[j]*i>N) break;
            check[prime[j]*i] = true;
            if(i%prime[j]) g[prime[j]*i] = g[prime[j]]*g[i];
            else {g[prime[j]*i]=g[i]; break;}
        }
    }
}

void get_t()
{
    for(int k=2 ; k<=N ; k++)
        for(int i=k ; i<=N ; i+=k)
            t[i] = (t[i]+g[k-1])%MOD;
}

void get_f()
{
    for(int i=1 ; i<=N ; i++)
        f[i] = (f[i-1]+2*i-1-t[i-1])%MOD;
}

void init()
{
    get_g();
    get_t();
    get_f();
    for(int i=1 ; i<=N ; i++) sum[i] = (sum[i-1]+f[i])%MOD;
}

int main()
{
    //freopen("a.in" , "r" , stdin);
    init();
    int T , n;
    scanf("%d" , &T);
    while(T--){
        scanf("%d" , &n);
        printf("%I64d\n" , sum[n]);
    }
    return 0;
}