bzoj1211(洛谷P2290) - [HNOI2004]树的计数
Author : hiang
Description
一个有n个结点的树，设它的结点分别为v1, v2, …, vn，已知第i个结点vi的度数为di，问满足这样的条件的不同的树有多少棵。给定n，d1, d2, …, dn，编程需要输出满足d(vi)=di的树的个数。
Input
第一行是一个正整数n，表示树有n个结点。第二行有n个数，第i个数表示di，即树的第i个结点的度数。其中1<=n<=150，输入数据保证满足条件的树不超过10^17个。
Output
输出满足条件的树有多少棵。
Sample Input
2 1 2 1
Sample Output
如果了解prufer编码的话本题很容易解决，在这里详细介绍一下prufer编码的原理
prufer编码用于表示一颗带编号的无根树，它与无根树是一一对应的关系，即对于一棵n个节点的无根树，对应唯一长度为n-2的prufer编码
编码方式为：
选取叶子中编号最小的点，将这个点删除，并且把它的邻接点加到编码尾部，再在删去该点后形成的树中删除最小的叶子节点，并把邻接点加到编码尾部，重复以上步骤，直到树中只剩下两个点，就形成了prufer编码
例如：
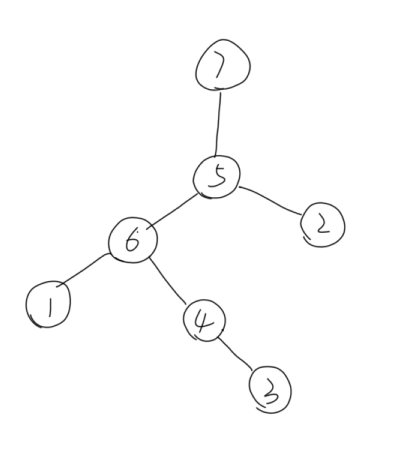
该树中叶子节点编号最小的为1，所以将1删去，将6加到编码中，此时编码为6
新树中叶子节点编号最小的为2，所以将2删去，将5加到编码中，此时编码为6，5
新树中叶子节点编号最小的为3，所以将3删去，将4加到编码中，此时编码为6，5，4
以此类推，得到最后形成的prufer编码为6，5，4，6，5
最后剩余的两个点不参与编码，所以编码长度为n-2，可以发现，一开始为叶子的节点编号并不会出现在编码中，其他节点都出现了本身的度数减一次，而prufer编码和无根树之间是一一对应关系，所以要想求解上述问题，只需要求一个多重集的全排列数即可
已知n个节点，第i个节点vi的度数为di，从所有节点中选出n-2个，每一个出现次数为di-1，易知全排列数为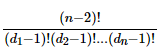
（可能有不会求多重集全排列数的，这里提供公式推导过程：
已知有k个不同的数a1，a2...ak，每个数分别有n1，n2...nk个，总数为n，先在n个位置中先选择n1个位置放a1，有C(n,n1)种方法，再在剩下的n-n1个位置选择n2个位置放a2，有C(n-n1,n2)种方法...最后在n-n1-n2-…nk-1个位置中选择nk个位置放ak，有C(n-n1-n2-…nk-1,nk)种方法,全部乘起来得全排列数：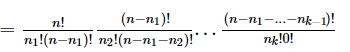
） 1 #include<bits/stdc++.h>
2 using namespace std;
3 int n;
4 long long d[155],cnt[155];
5 void prime(int x,int k)
6 {
7 int i=2;
8 while(x>1)
9 {
10 if(x%i==0)
11 {
12 cnt[i]+=k;
13 x/=i;
14 }
15 else i++;
16 }
17 }
18 int main()
19 {
20 long long sum=1;
21 int i,j,ans=0;
22 scanf("%d",&n);
23 for(i=1;i<=n;i++)
24 {
25 scanf("%lld",&d[i]);
26 if(d[i]>1)
27 ans+=d[i]-1;
28 }
29 if(n==1)
30 {
31 if(d[1]==0)
32 printf("1");
33 else
34 printf("0");
35 return 0;
36 }
37 if(ans!=n-2)
38 {
39 printf("0");
40 return 0;
41 }
42 for(i=2;i<=n-2;i++)
43 prime(i,1);
44 for(i=1;i<=n;i++)
45 for(j=2;j<=d[i]-1;j++)
46 prime(j,-1);
47 for(i=1;i<=n;i++)
48 while(cnt[i]>0)
49 {
50 sum*=i;
51 cnt[i]--;
52 }
53 printf("%lld",sum);
54 return 0;
55 }
