解决动态连通性——并查集
先贴一个大佬的文章，解释有趣简单，非常适合新人~
不过这个原帖的阅读量还没有几个转发的高……唉
什么是并查集？并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。常常在使用中以森林来表示。在实际解决问题的过程中并查集的应用广泛，但主要还是用来判断两点是否联通，以及寻找一个节点的祖先。
下面我们通过一个例子来简单了解一下并查集。
houge，hiang，revolver是UJN的三名大一新生。其中，houge和hiang在计1801班，班长是宋同学，班主任是曲老师；revolver在计1802班，班长是张同学，班主任是王老师，我们就可以据此得到一个关系图
现在我们想找一下houge和revolverz的最大的上级：首先houge的直接上级是宋同学，宋同学的上级是曲老师；revolverz的直接上级是张同学，张同学的上级是王老师。这样一来，我们的任务就完成了。但是我们每次想要找一个同学最大的上级的时候都需要经过中间人，这样太麻烦了，我们不如把每个同学的直接上级都改为他的最大上级，这样就方便了许多。
改完之后我们发现houge，hiang和revolverz虽然在一个队伍里，却不在一个班级里，好在大二分流之后重新分班，要把计1802的同学全部加入到计1801里。我们把计1802班级里的所有人的上级，都改为曲老师，这样R神就和我们一个班了！但是有什么用呢？他已经退役了。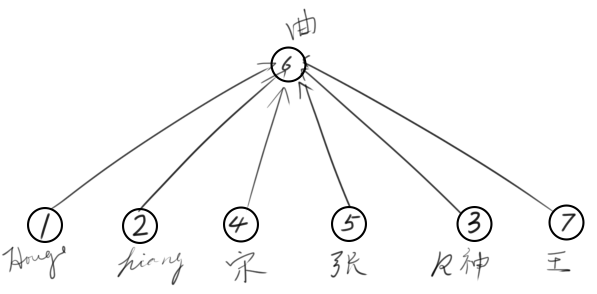
我们还会发现王老师的上级竟然变成了曲老师，没办法，谁让计1802班合并了呢 XD
上面这个过程就简单实现了并查集的三个操作：查询、路径压缩和合并。
下面我们试着用代码来实现上面的过程。
一、查询
首先我们需要一个数组pre[]来记录当前结点的父结点，如该结点没有父结点，我们让pre[this]等于它本身。如对于上面的例子，我们可以赋值：pre[1]=pre[2]=4,pre[4]=6,pre[6]=6,pre[3]=5,pre[5]=7,pre[7]=7。
若要查询一个结点的根结点，我们要查询它的父结点，在查询父结点的父结点……直到一个结点的父结点就是他本身为止（pre[i]=i），代码如下：
1 int union_find(int x) 2 { 3 int r=x; 4 while(r!=pre[r]) 5 { 6 r=pre[r]; 7 } 8 return r; 9 }
同时我们也可以查询两个不同的结点是否在同一个通路里面，只需要判断一下两个结点的根结点是否相同即可，这一步的代码与合并一起在下面给出。
二、路径压缩
虽然查询操作的耗时不算大，但是当你的一个结点和它的根结点之间有很多的中间结点，而且查询的次数非常多的时候，就可能会耗费非常多的时间。那么我们可以在每一次的查询过程中，都进行路径压缩，把一个结点的父结点直接改为根结点，来达到防止浪费时间的目的。
1 int union_find(int x) 2 { 3 int r=x; 4 while(r!=pre[r]) 5 { 6 r=pre[r]; 7 } 8 int i=x,j; 9 while(pre[i]!=r) //路径压缩 10 { 11 j=pre[i]; 12 pre[i]=r; 13 i=j; 14 } 15 return r; 16 }
三、合并
对于两个在不同通路的结点，若想把它们合并为一个通路，只需要把一个结点设为另一个点的父结点即可（无特殊需要，没有顺序要求）。
1 void join(int a,int b) 2 { 3 int u,v; 4 u=union_find(a); 5 v=union_find(b); 6 if(u!=v) pre[u]=v; 7 }
这样我们就把并查集的基本功能都实现了，下面来看一些题目。
四、相关应用及题目
1.例题 Luogu P3367【模板】并查集
代码：
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 int pre[10005]; 6 7 int union_find(int x) 8 { 9 int r=x; 10 while(r!=pre[r]) 11 { 12 r=pre[r]; 13 } 14 int i=x,j; 15 while(pre[i]!=r) 16 { 17 j=pre[i]; 18 pre[i]=r; 19 i=j; 20 } 21 return r; 22 } 23 24 void join(int a,int b) 25 { 26 int u,v; 27 u=union_find(a); 28 v=union_find(b); 29 if(u!=v) pre[u]=v; 30 } 31 32 int main() 33 { 34 int n,m; 35 scanf("%d%d",&n,&m); 36 for(int i=0;i<=n;i++) pre[i]=i; 37 while(m--) 38 { 39 int x,y,z; 40 scanf("%d%d%d",&z,&x,&y); 41 if(z==1) join(x,y); 42 else 43 { 44 int a,b; 45 a=union_find(x); 46 b=union_find(y); 47 if(a==b) printf("Y\n"); 48 else printf("N\n"); 49 } 50 } 51 return 0; 52 }
2.最小生成树——Kruskal
在Kruskal中我们利用并查集来判断目前所选边的两点是否已经连通。
相关链接：求最小生成树——Kruskal
五、其他题目
Author : Houge Date : 2019.6.4
Update log :
