求最小生成树——Kruskal

Kruskal（克鲁斯卡尔）算法：

“求加权连通图的最小生成树的算法。”

　　　　　　　　　　　　　　——百度百科

一、什么是Kruskal

 

我们直接来看Kruskal算法的实现思想：
　　对于每一条边，按权值从小到大排序，然后遍历。判断一条边的两点是否已经连通，若未连通，则把这条边加入图中，否则继续判断下一条边，直到构建出最小生成树。（一种贪心算法的应用）

 

看完上面，不知道你理解了吗？不管是否明白，我们下面结合一个例子再看一遍Kruskal是如何实现的。

 

对于下面的图，它有6个点和9条边，每条边上有相应的权值，不过目前这些边都还没有加入到图中。

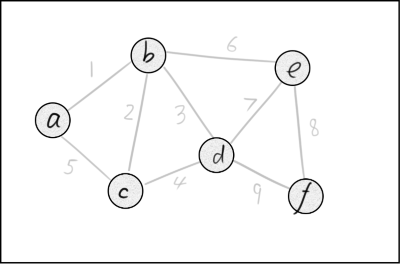
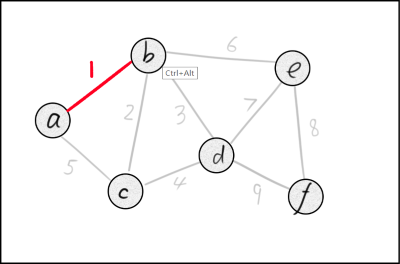
首先我们从权值为1的边看起（按权值从小到大），很显然，它的两个点还没有连通，我们把它加入图中。

 

同样，我们接着把权值为2、3的两条边加入到图中。

 

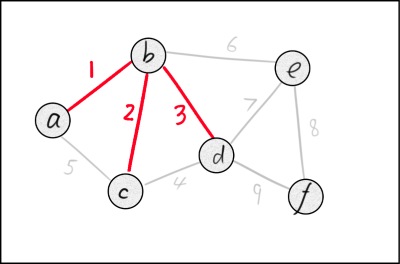
然而在判断权值为4的边的时候，要小心，它的两端点已经连通（c→b→d），所以我们跳过这条边。

 

同理，我们接下来跳过权值为5、7、9的边，且将权值为6、8的边加入到图中，得到了我们的最小生成树。

 

相信通过上面的例子，你对Kruskal已经有了更深的理解，现在我们来思考如何用代码实现我们在上面模拟的过程。

 

二、如何实现Kruskal

首先我们先要解决两个问题：

　　①如何表示这些边、点及边的权值。

　　②如何判断两个点是否连通。

要解决这两个问题，我们需要两个工具：

·一个结构体，用来储存边的信息： 

struct edge
{
    int start,to,value;    //起点、终点和权值，value的值可以不是整型
    bool operator <(edge a)const    //重载运算符，作用相当于一个cmp函数
    {
        return value<a.value;
    }
}e[num_edge];

 ·利用并查集，来判断点是否连通：

（如还未学习并查集，可点此跳转学习）

int union_find(int x)
{
    int r=x;
    while(pre[r]!=r)    //寻找祖先。这样的话，我们就需要一个pre数组记录这个点的祖先
    {
        r=pre[r];
    }
    int i=x,j;
    while(i!=r)    //路径压缩，可不加
    {
        j=pre[i];
        pre[i]=r;
        i=j;
    }
    return r;
}

有了这两个工具，我们就可以用代码来实现Kruskal了：

void kruskal()
{
    int i;
    total=0;    //记录已经加入图中的边的数量
    val=0;    //记录权值之和
    for(i=0;i<m;i++)    //遍历边
    {
        int u,v;
        u=union_find(e[i].start);
        v=union_find(e[i].to);
        if(u==v) continue;    //判断这个边的两点是否连通，如连通，则跳过
        total++;
        pre[u]=v;    //将两点更新为连通
        val+=e[i].value;
        if(total==n-1) break;    //若total=n-1则已经生成最小生成树，可跳出循环了
    }
    return ;
}

 至此，相信你已经成功入门Kruskal了~

 

三、相关题目

例题：Luogu P3366【模板】最小生成树

代码：

#include <bits/stdc++.h>

using namespace std;

int pre[5005],n,m,val,total;

struct edge
{
    int start,to,value;
    bool operator <(edge a)const
    {
        return value<a.value;
    }
}e[200005];

int union_find(int x)
{
    int r=x;
    while(pre[r]!=r)
    {
        r=pre[r];
    }
    int i=x,j;
    while(i!=r)
    {
        j=pre[i];
        pre[i]=r;
        i=j;
    }
    return r;
}

void kruskal()
{
    int i;
    total=0;
    val=0;
    for(i=0;i<m;i++)
    {
        //cout<<"test"<<' ';
        int u,v;
        u=union_find(e[i].start);
        v=union_find(e[i].to);
       // cout<<u<<' '<<v<<'*'<<endl;
        if(u==v) continue;
        total++;
        pre[u]=v;
        val+=e[i].value;
        if(total==n-1) break;
    }
}

int main()
{
    int i;
    scanf("%d%d",&n,&m);
    for(i=0;i<n;i++) pre[i]=i;
    for(i=0;i<m;i++) scanf("%d%d%d",&e[i].start,&e[i].to,&e[i].value);
    sort(e,e+m);
    kruskal();
    //cout<<total<<'*'<<endl;
    if(total==n-1) printf("%d",val);
    else printf("orz");
    return 0;
}

 

其他题目：

Luogu P2330 [SCOI2005]繁忙的都市（难度：☆）

Luogu P2872 [USACO07DEC]道路建设Building Roads（难度：★）

Luogu P2504 [HAOI2006]聪明的猴子（难度：★）

Luogu P2212 [USACO14MAR]浇地Watering the Fields（难度：★☆）

 

Author : Houge　　Date : 2019.5.25

Update log :

2019.5.28：修改了文章结构，使文章更加易懂。