LCS+完全背包
1、问题
LCS：给定序列X=<x1,x2,...,xm>,Y=<y1,y2,...,yj>,求X和Y的最长公共子序列。
完全背包：一个旅行者准备随身携带一个背包。可以放入背包的物品有 n 种，物品 j 的重量和价值分别为Wj，Vj，j=1,2,...,n 。如果背包的最大重量限制是 b，怎么选择放入背包物品以使得背包的价值最大。
2、解析
LCS:
转移方程
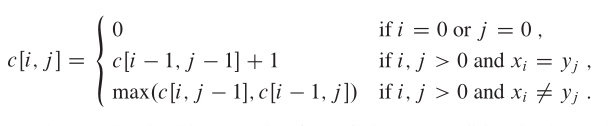
过程推导
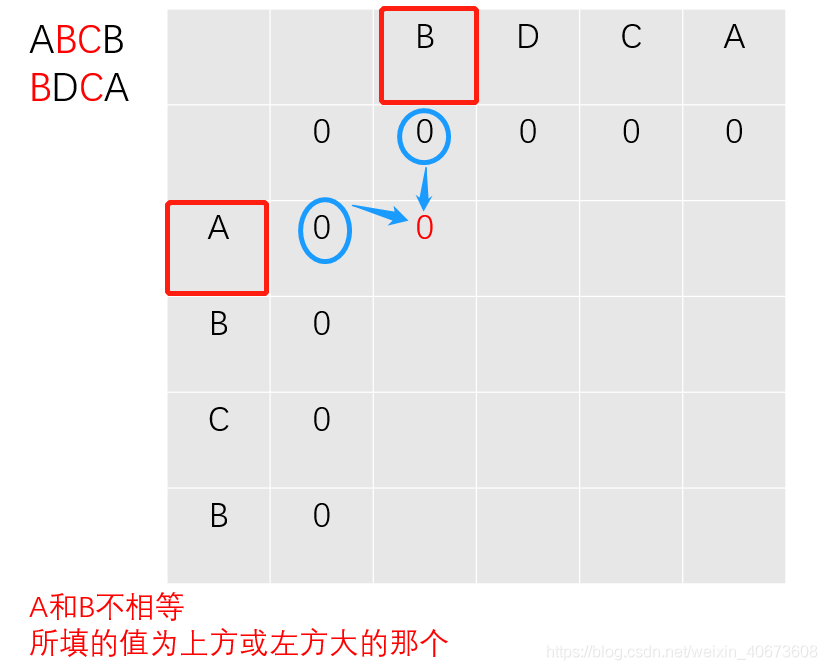
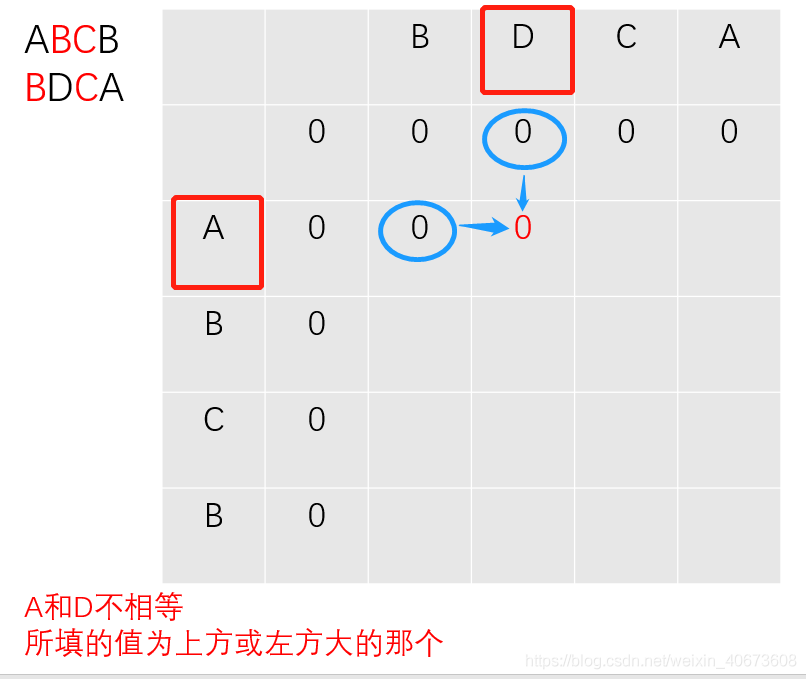
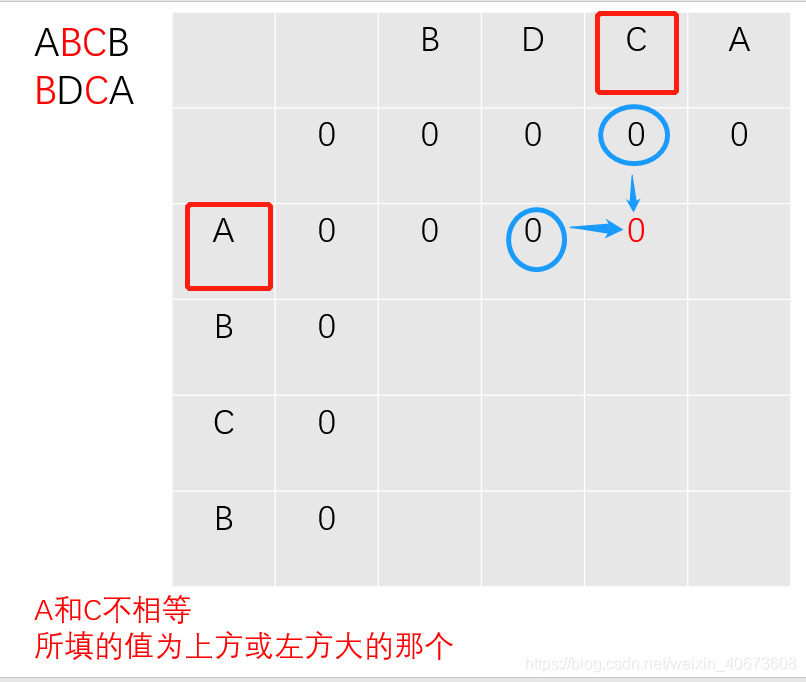
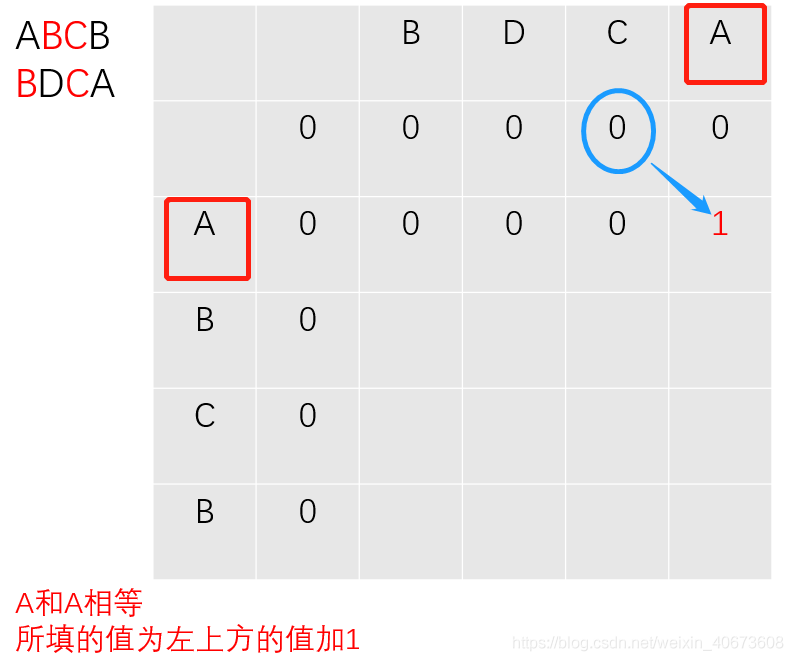
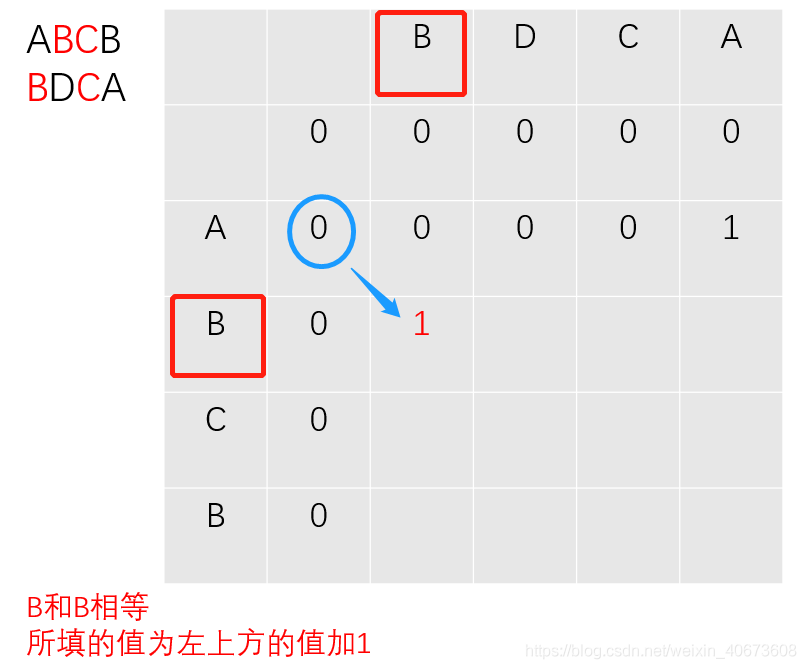
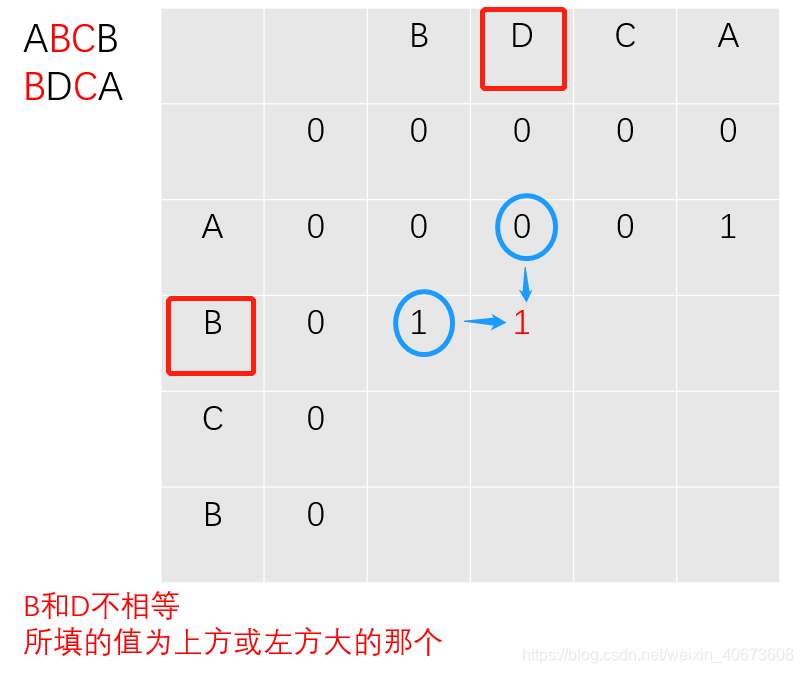
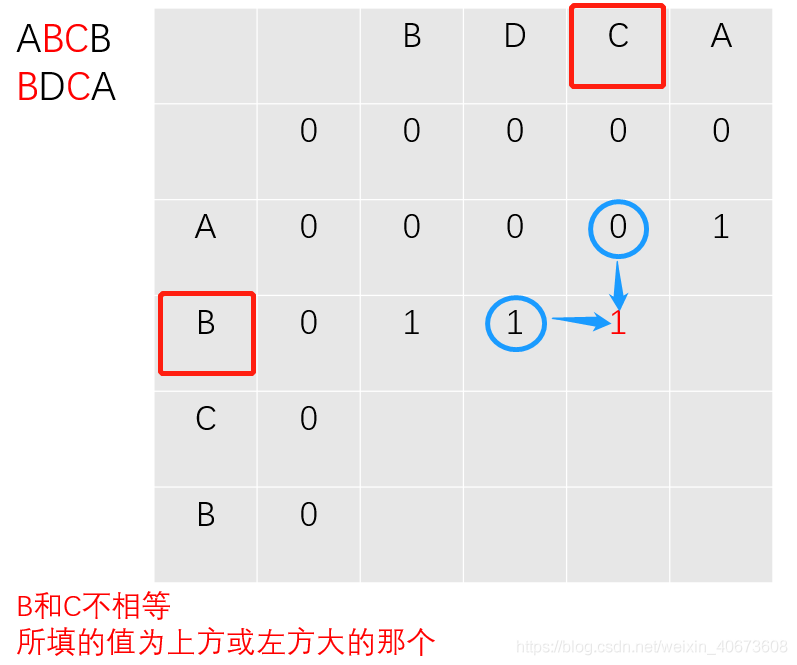
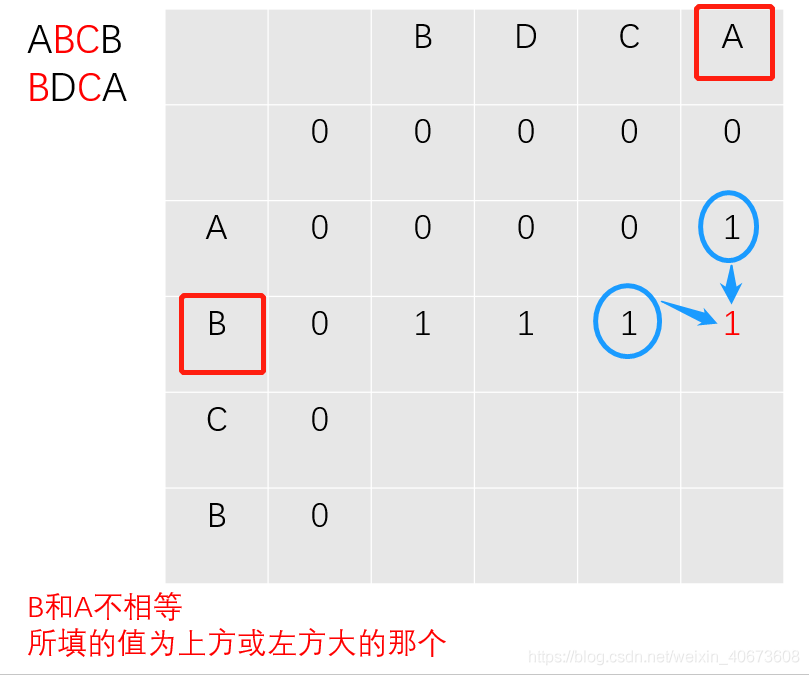
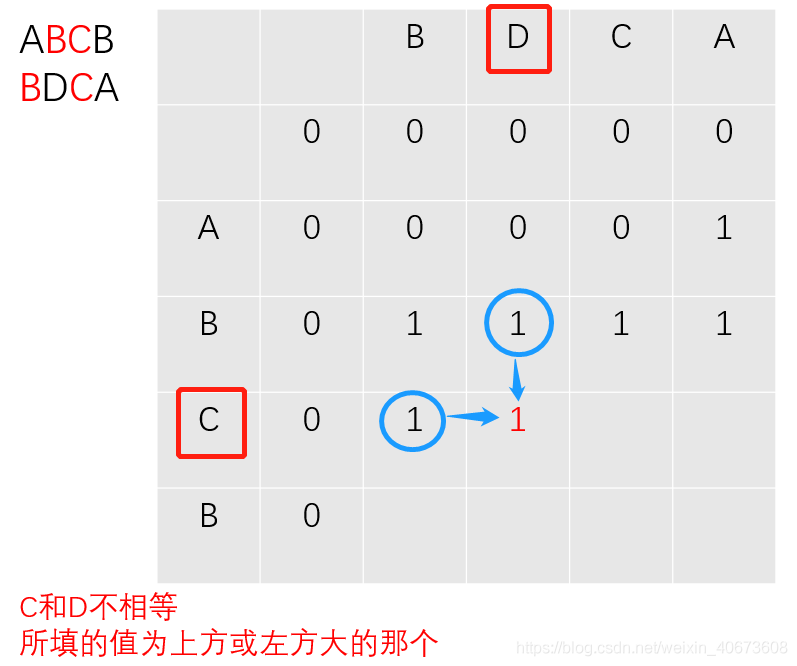
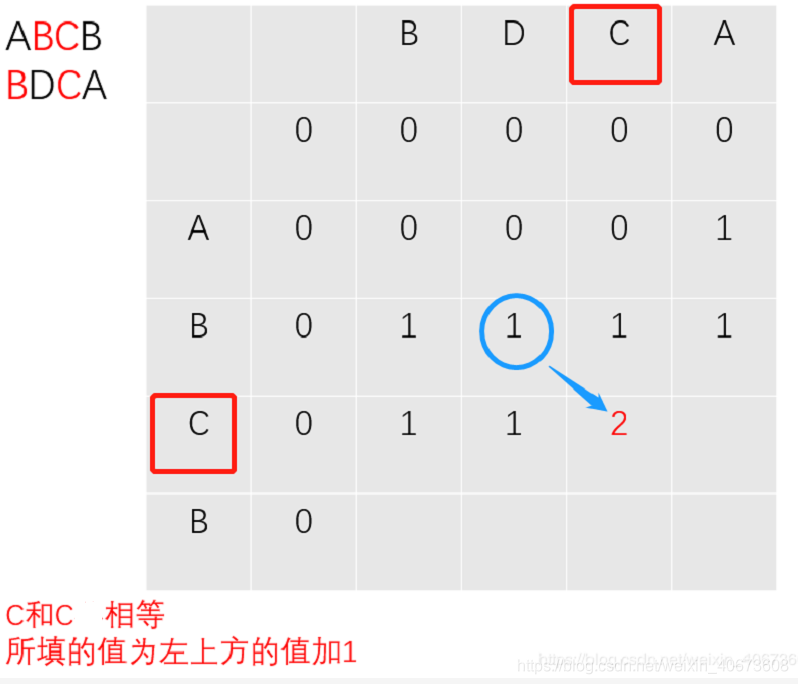
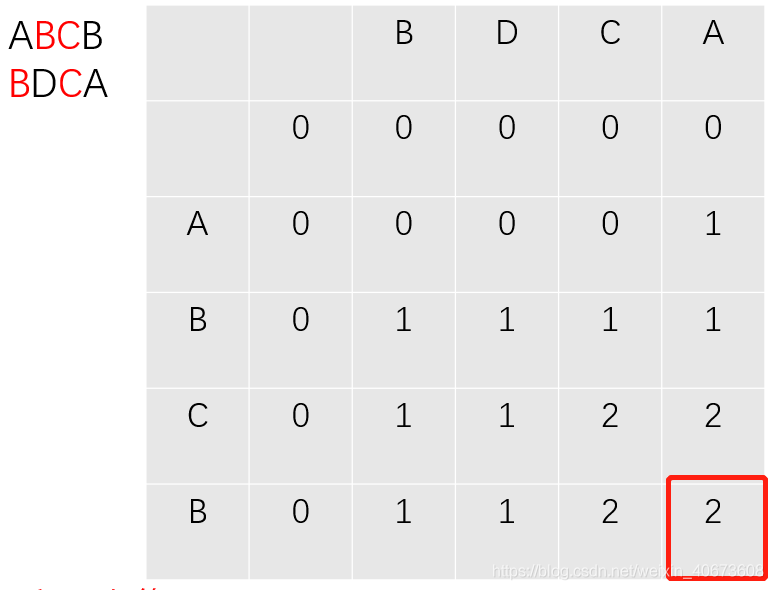
完全背包：
转移方程
推导过程
3、设计
1 void LCS(int l,int r) {//输出方案 2 if l<=0 or r<=0 3 return; 4 if a[l] == b[r] 5 LCS(l-1,r-1) 6 cout<<a[l] 7 else if dp[l-1][r] > dp[l][r-1] 8 LCS(l-1,r) 9 else 10 LCS(l,r-1) 11 } 12 13 for i <- 1 to lena //转移过程 14 for j <- 1 to lenb 15 if a[i] == b[j] 16 dp[i][j] <- dp[i-1][j-1] + 1 17 else 18 dp[i][j] <- max(dp[i-1][j],dp[i][j-1])
1 cin>>n>>m; 2 for i <- 1 to n 3 cin>>w[i]>>v[i] 4 for i <- 1 to n 5 for j <- w[i] to m 6 dp[j] <- max(dp[j],dp[j-w[i]]+v[i]) 7 cout<<dp[m]<<endl;
4、分析
LCS需要两重循环DP，第一重为串A的长度O(N)，第二重为串B的长度O(N)，所以时间复杂度为O(N^2)
完全背包需要两重循环DP，第一重为物品数量O(N)，第二重为背包容量O(W)，所以时间复杂度为O(N*W)
5、源码
LCS
https://github.com/ChenyuWu0705/Algorithm-Analyze-and-Design/blob/main/LCS.cpp
完全背包
https://github.com/ChenyuWu0705/Algorithm-Analyze-and-Design/blob/main/complete%20bag.cpp
