最小生成树 (Prim和Kruskal)
1、问题
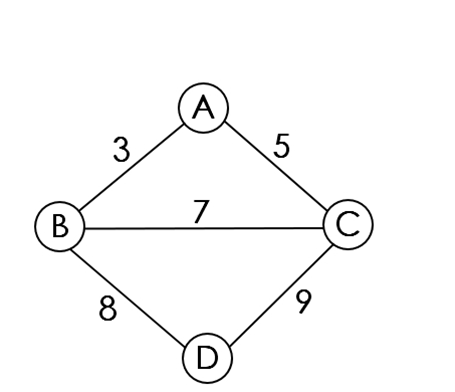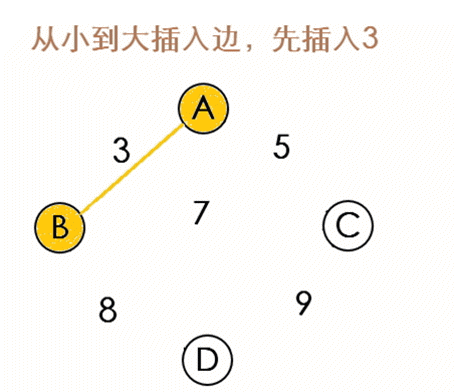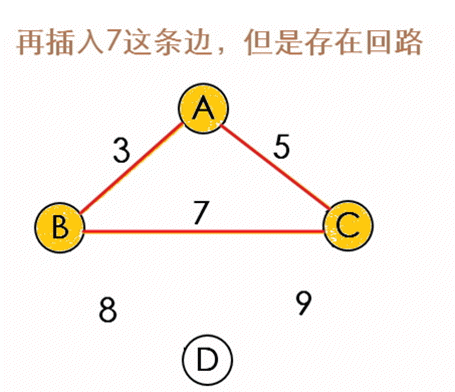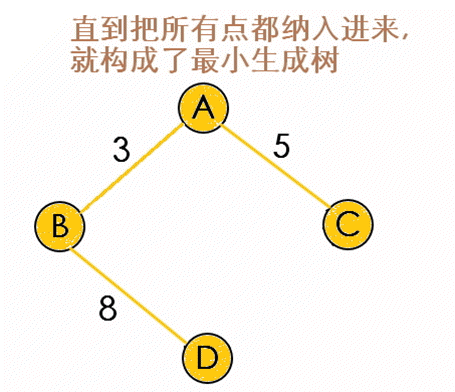
在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边，而 w(u, v) 代表此边的权重，求存在 T 为 E 的子集且为无循环图，使得的 w(T) 最小。
2、解析
Prim算法实现步骤:
1、随机取一个点设为起点，加入到集合S中
2、找到一个不属于集合S的点P，且该点距离集合S最近
3、将点P加入到集合S中，并松弛所有和点P相连且未加入集合S的点
4、重复步骤2、3直接所有点都加入到集合S
Kruskal算法实现步骤:
1、将所有边加入到集合S中
2、选择一条未选择过的最短边(u,v),若点u和点v不属于同一个集合，将点u并入点v的集合(该操作用并查集实现)
3、重复步骤2，直到将n-1条边加入到最小生成树
3、设计
Prim算法伪代码：
1 int Prim(int graph[][N], bool vis[], int dis[],int n) { 2 //graph[]里面存储的是点之间的距离 3 //dis[]存储的是初始点到各点的距离 4 //vis[]存储该点是否被标记过 5 //n代表点的个数 6 7 ans <- 0;//最小生成树的权值和 8 9 for i <- 1 to n //初始化操作 10 vis[i] = false; 11 dis[i] = graph[1][i]; 12 13 vis[1] <- true//标记初始点 14 for i <- 2 to n 15 minn <- 0x3f3f3f3f 16 index <- -1 17 for j <- 1 to n 18 if vis[j] <- false and dis[j] < minn 19 //寻找未标记点集合中距离已标记点集合最近的点，若找到，记录下标，修改minn 20 minn <- dis[j] 21 index <- j 22 if index == -1//未找到可以进行标记的点，说明该图不连通 23 return -1 24 25 vis[index] <- true//找到的点打上标记 26 ans <- ans+minn//加上该段距离的权值 27 for (j <- 1 to n 28 //通过找到的点对所有未标记的点进行松弛操作 29 if vis[j] == false and graph[index][j] < dis[j] 30 dis[j] <- graph[index][j] 31 return ans//返回权值和 32 }
Kruskal算法伪代码：
1 int find(int x){ 2 if x==fa[x] 3 return x 4 else 5 return fa[x] <- find(fa[x]) 6 //路径压缩+查找祖先节点 7 } 8 9 int kruskal(){ 10 ans <- 0 11 cnt <- 0 12 sort(edge, edge + m, cmp)//给边排序 13 for i = 0 to m 14 fu = find(edge[i].u)//查找顶点u的祖先节点 15 fv = find(edge[i].v)//查找顶点v的祖先节点 16 if fu != fv //如果不构成环，在MST中加上该条边 17 ans <- ans + edge[i].w 18 fa[fv] = fu//跟新顶点v的父节点 19 cnt <- cnt + 1 20 if cnt == n - 1 21 return ans// 找到MST返回MST的权值 22 return -1 23 }
4、分析
Prim算法时间复杂度分析：
进行n次加入集合操作，时间复杂度O(n)
在n次操作中，查找最近的点操作，时间复杂度O(n)；松弛所有未标记的点,时间复杂度O(n)
总时间复杂度O(n^2)
Kruskal算法时间复杂度分析：
m条边使用sort升序排序时间复杂度O(m*log(m))
往空图中加入m条边时间复杂度O(m)，每加入一条边用并查集判断是否构成环，路径压缩并查集查找祖先节点时间复杂度O(log(m))
总时间复杂度O(m*log(m))
5、源码
https://github.com/ChenyuWu0705/Algorithm-Analyze-and-Design/blob/main/Kruskal.cpp
https://github.com/ChenyuWu0705/Algorithm-Analyze-and-Design/blob/main/Prim.cpp
