【BZOJ2401】陶陶的难题I 欧拉函数+线性筛
【BZOJ2401】陶陶的难题I
题意:求 ,n<=1000000,T<=100000
,n<=1000000,T<=100000
题解:直接做是n*sqrt(n)的,显然会TLE,不过这题a和b都是循环到n,那么就可以进行如下的神奇变换:
$\sum\limits_{i=1}^n\sum\limits_{j=1}^nlcm(i,j)=2*\sum\limits_{i=1}^n\sum\limits_{j=1}^ilcm(i,j)-\sum\limits_{i=1}^ni$
是不是很神奇?然后继续推即可。
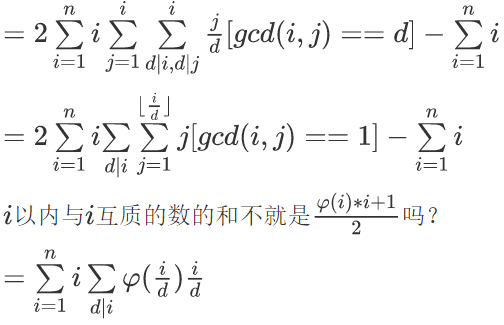
设$f(i)=\sum\limits_{d|i}\varphi({i\over d}){i\over d}$,我们只需要现行筛出f即可。
我们依旧只考虑i是质数的情况,当i=p时,$f(i)=p^2-p+1$,当i=p^2时,$f(i)=p^4-p^3+p^2-p+1$,以此类推。
所以我们维护一下x的最小质因子出现的次数,然后线性筛即可。
还有,因为出题人丧病,此题爆long long。
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;
const int N=1000000;
const ll P=1000000000000ll;
ll a,b;
int n,num,T;
int np[N+10],pri[N/10],phi[N+10];
ll g[N+10],h[N+10];
struct lll
{
ll a,b;
lll() {a=b=0;}
lll(ll c) {a=c/P,b=c%P;}
lll(ll x,ll y){a=x,b=y;}
lll operator + (const lll &x) const
{
lll y(a+x.a,b+x.b);
y.a+=y.b/P,y.b%=P;
return y;
}
lll operator - (const lll &x) const
{
lll y(a-x.a,b-x.b);
if(y.b<0) y.a--,y.b+=P;
return y;
}
void print()
{
if(a) printf("%lld%012lld\n",a,b);
else printf("%lld\n",b);
}
}f[N+10];
inline ll rd()
{
ll ret=0,f=1; char gc=getchar();
while(gc<'0'||gc>'9') {if(gc=='-')f=-f; gc=getchar();}
while(gc>='0'&&gc<='9') ret=ret*10+gc-'0',gc=getchar();
return ret*f;
}
int main()
{
int i,j,p;
g[1]=1;
for(i=2;i<=N;i++)
{
if(!np[i]) pri[++num]=i,g[i]=h[i]=(ll)i*i-i+1;
for(j=1;j<=num&&i*pri[j]<=N;j++)
{
p=pri[j],np[i*p]=1;
if(i%p==0)
{
h[i*p]=h[i]*p*p-p+1;
g[i*p]=g[i]/h[i]*h[i*p];
break;
}
h[i*p]=(ll)p*p-p+1;
g[i*p]=g[i]*h[i*p];
}
}
for(i=1;i<=N;i++) f[i]=lll(g[i]*i)+f[i-1];
T=rd();
while(T--)
{
ll n=rd();
lll ans=f[n];
ans.print();
}
return 0;
}
| 欢迎来原网站坐坐! >原文链接<


