【BZOJ3561】DZY Loves Math VI 莫比乌斯反演

【BZOJ3561】DZY Loves Math VI

Description

给定正整数n,m。求

 

Input

一行两个整数n,m。

Output

一个整数，为答案模1000000007后的值。

Sample Input

5 4

Sample Output

424

HINT

数据规模：
1<=n,m<=500000，共有3组数据。

题解：没啥说的，摆式子：

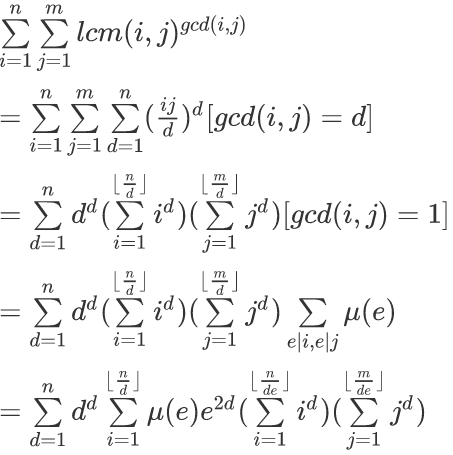
推到这就行啦！因为n,m只有500000，所以用调和级数把上面的东西求一下就行了。

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;
const ll P=1000000007;
const int maxn=500010;
int np[maxn],pri[maxn/10],mu[maxn];
ll d[maxn],s[maxn];
inline ll pm(ll x,ll y)
{
	ll z=1;
	while(y)
	{
		if(y&1)	z=z*x%P;
		x=x*x%P,y>>=1;
	}
	return z;
}
ll ans,D;
int n,m,num,i,last,j;
int main()
{
	scanf("%d%d",&n,&m);
	if(n>m)	swap(n,m);
	mu[1]=1;
	for(i=2;i<=m;i++)
	{
		if(!np[i])	pri[++num]=i,mu[i]=-1;
		for(j=1;j<=num&&i*pri[j]<=m;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				mu[i*pri[j]]=0;
				break;
			}
			mu[i*pri[j]]=-mu[i];
		}
	}
	for(i=1;i<=m;i++)	d[i]=1;
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=m/i;j++)	d[j]=d[j]*j%P,s[j]=(s[j-1]+d[j])%P;
		D=pm(i,i);
		for(j=1;j<=m/i;j++)	ans=(ans+D*mu[j]*d[j]%P*d[j]%P*s[n/(i*j)]%P*s[m/(i*j)]%P+P)%P;
	}
	printf("%lld",ans);
	return 0;
}