【BZOJ4407】于神之怒加强版 莫比乌斯反演
【BZOJ4407】于神之怒加强版
Description
给下N,M,K.求

Input
输入有多组数据,输入数据的第一行两个正整数T,K,代表有T组数据,K的意义如上所示,下面第二行到第T+1行,每行为两个正整数N,M,其意义如上式所示。
Output
如题
Sample Input
1 2
3 3
3 3
Sample Output
20
HINT
1<=N,M,K<=5000000,1<=T<=2000
题解:如何快速推出线性筛的递推式呢?——打表。
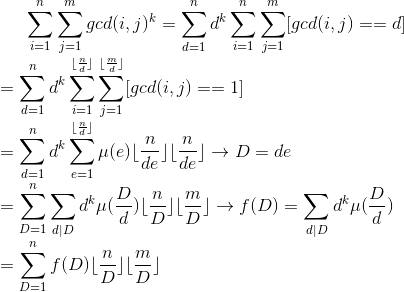
发现f(D)长得跟$\varphi(D)$差不多?所以递推式也差不多
$f(i*pj)=\begin{cases}& f(i)*(pj^k-1) & i\%pj!=0 \\ & f(i)*pj^k & i\%pj==0\end{cases}$
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
const int N=5000000;
int T,k,num;
int pri[N];
ll f[N+10],sf[N+10],pk[N],ans;
bool np[N+10];
ll pm(ll x,ll y)
{
ll z=1;
while(y)
{
if(y&1) z=z*x%mod;
x=x*x%mod,y>>=1;
}
return z;
}
void init()
{
int i,j;
f[1]=sf[1]=1;
for(i=2;i<=N;i++)
{
if(!np[i]) pri[++num]=i,pk[num]=pm(i,k),f[i]=pk[num]-1;
sf[i]=sf[i-1]+f[i];
for(j=1;j<=num&&i*pri[j]<=N;j++)
{
np[i*pri[j]]=1;
if(i%pri[j]==0)
{
f[i*pri[j]]=f[i]*pk[j]%mod;
break;
}
f[i*pri[j]]=f[i]*(pk[j]-1)%mod;
}
}
}
void work()
{
int n,m,i,last;
ans=0;
scanf("%d%d",&n,&m);
if(n>m) swap(n,m);
for(i=1;i<=n;i=last+1)
{
last=min(n/(n/i),m/(m/i));
ans=(ans+(sf[last]-sf[i-1])*(n/i)%mod*(m/i)%mod)%mod;
}
printf("%lld\n",(ans+mod)%mod);
}
int main()
{
scanf("%d%d",&T,&k);
init();
while(T--) work();
return 0;
}
| 欢迎来原网站坐坐! >原文链接<


