【BZOJ2226】[Spoj 5971] LCMSum 莫比乌斯反演(欧拉函数?)
【BZOJ2226】[Spoj 5971] LCMSum
Description
Given n, calculate the sum LCM(1,n) + LCM(2,n) + .. + LCM(n,n), where LCM(i,n) denotes the Least Common Multiple of the integers i and n.
Input
The first line contains T the number of test cases. Each of the next T lines contain an integer n.
Output
Output T lines, one for each test case, containing the required sum.
Sample Input
3
1
2
5
1
2
5
Sample Output
1
4
55
4
55
HINT
Constraints
1 <= T <= 300000
1 <= n <= 1000000
题解:好吧我naive了,别人都用欧拉函数就我用莫比乌斯反演,还是写一发吧~
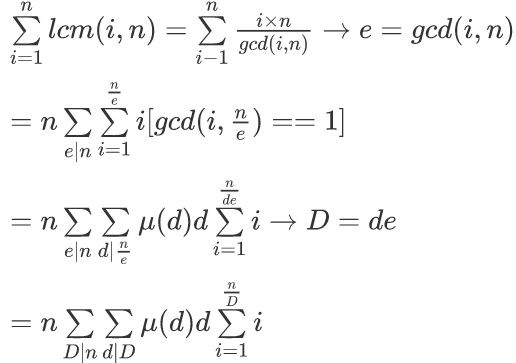
然后线性筛∑μ(d)d,然后O(nlogn)枚举n的约数就行了
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
const int m=1000000;
typedef long long ll;
int n,T,num,tot;
int pri[m/10],to[m*14],next[m*14],head[m+10];
bool np[m+10];
vector<int> v[m+10];
ll sm[m+10],ans;
int main()
{
int i,j;
for(i=1;i<=m;i++) for(j=i;j<=m;j+=i) to[++tot]=i,next[tot]=head[j],head[j]=tot;
sm[1]=1;
for(i=2;i<=m;i++)
{
if(!np[i]) pri[++num]=i,sm[i]=1-i;
for(j=1;j<=num&&i*pri[j]<=m;j++)
{
np[i*pri[j]]=1;
if(i%pri[j]==0)
{
sm[i*pri[j]]=sm[i];
break;
}
sm[i*pri[j]]=sm[i]*(1ll-pri[j]);
}
}
scanf("%d",&T);
while(T--)
{
scanf("%d",&n),ans=0;
for(i=head[n];i;i=next[i]) ans+=sm[n/to[i]]*to[i]*(to[i]+1)>>1;
printf("%lld\n",ans*n);
}
return 0;
}
| 欢迎来原网站坐坐! >原文链接<


