【BZOJ3083/3306】遥远的国度/树 树链剖分+线段树

【BZOJ3083】遥远的国度

Description

描述
zcwwzdjn在追杀十分sb的zhx，而zhx逃入了一个遥远的国度。当zcwwzdjn准备进入遥远的国度继续追杀时，守护神RapiD阻拦了zcwwzdjn的去路，他需要zcwwzdjn完成任务后才能进入遥远的国度继续追杀。

问题是这样的：遥远的国度有n个城市，这些城市之间由一些路连接且这些城市构成了一颗树。这个国度有一个首都，我们可以把这个首都看做整棵树的根，但遥远的国度比较奇怪，首都是随时有可能变为另外一个城市的。遥远的国度的每个城市有一个防御值，有些时候RapiD会使得某两个城市之间的路径上的所有城市的防御值都变为某个值。RapiD想知道在某个时候，如果把首都看做整棵树的根的话，那么以某个城市为根的子树的所有城市的防御值最小是多少。由于RapiD无法解决这个问题，所以他拦住了zcwwzdjn希望他能帮忙。但zcwwzdjn还要追杀sb的zhx，所以这个重大的问题就被转交到了你的手上。

Input

第1行两个整数n m，代表城市个数和操作数。
第2行至第n行，每行两个整数 u v，代表城市u和城市v之间有一条路。
第n+1行，有n个整数，代表所有点的初始防御值。
第n+2行一个整数 id，代表初始的首都为id。
第n+3行至第n+m+2行，首先有一个整数opt，如果opt=1，接下来有一个整数id，代表把首都修改为id；如果opt=2，接下来有三个整数p1 p2 v，代表将p1 p2路径上的所有城市的防御值修改为v；如果opt=3，接下来有一个整数 id，代表询问以城市id为根的子树中的最小防御值。

Output

对于每个opt=3的操作，输出一行代表对应子树的最小点权值。

Sample Input

3 7
1 2
1 3
1 2 3
1
3 1
2 1 1 6
3 1
2 2 2 5
3 1
2 3 3 4
3 1

Sample Output

1
2
3
4
提示
对于20%的数据，n<=1000 m<=1000。
对于另外10%的数据，n<=100000，m<=100000，保证修改为单点修改。
对于另外10%的数据，n<=100000，m<=100000，保证树为一条链。
对于另外10%的数据，n<=100000，m<=100000，没有修改首都的操作。
对于100%的数据，n<=100000，m<=100000，0<所有权值<=2^31。

题解：权值<=(1<<31)吓人~

一看到本题空间1280MB，第一反应就是先开它个2亿的数组再说~

如果没有换根操作，直接树剖线段树水过，但是就算有换根操作用树剖也是能搞的。

设当前根为root，想要查询x的子树中的最小值。考虑在原树中，如果x与root重合，那么答案就是整棵树的最小值；如果当前的root不在x原来的子树中，那么x现在的子树就是原来的子树，直接正常搞就行了。如果root在x原来的子树中，我们设root在x的ch儿子的子树中，发现x现在的子树就是（整棵树-ch原来的子树），那么我们需要知道ch的位置，此时又需要分类讨论了。

如果你没太看懂上面的叙述，可以通过看下面的图来理解一下。

这种情况显然直接搞

 

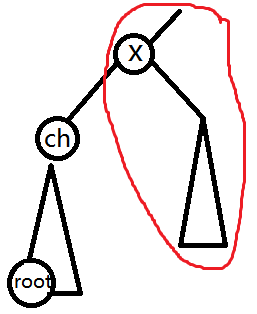这种情况我们要讨论

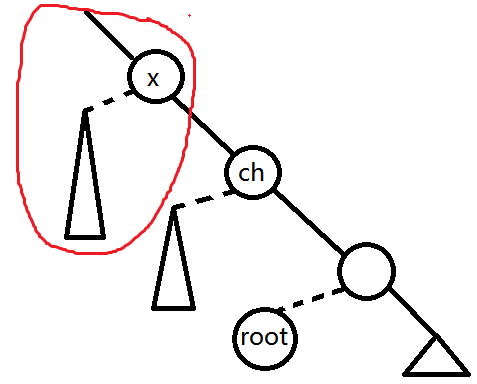我们看一下从root往上跳，在跳到x之前的最后一步，如果最后一步在重链上，那么ch的DFS序就是x的DFS序+1

如果最后一步在轻链上，那么跳最后一步之前的那个点就是ch

BZOJ3083

#include <cstdio>
#include <cstring>
#include <iostream>
#define lson x<<1
#define rson x<<1|1
using namespace std;
const int maxn=100010;
int n,m,cnt,root;
typedef unsigned int ll;
int to[maxn<<1],next[maxn<<1],head[maxn],dep[maxn],fa[maxn],son[maxn],top[maxn],p[maxn],q[maxn],v[maxn];
int siz[maxn],Q[maxn];
ll s[maxn<<2],tag[maxn<<2];
void pushdown(int x)
{
	if(tag[x])	s[lson]=tag[lson]=s[rson]=tag[rson]=tag[x],tag[x]=0;
}
void updata(int l,int r,int x,int a,int b,ll c)
{
	if(a<=l&&r<=b)
	{
		s[x]=tag[x]=c;
		return ;
	}
	pushdown(x);
	int mid=l+r>>1;
	if(a<=mid)	updata(l,mid,lson,a,b,c);
	if(b>mid)	updata(mid+1,r,rson,a,b,c);
	s[x]=min(s[lson],s[rson]);
}
ll query(int l,int r,int x,int a,int b)
{
	if(a>b)	return ((ll)1)<<31;
	if(a<=l&&r<=b)	return s[x];
	pushdown(x);
	int mid=l+r>>1;
	if(b<=mid)	return query(l,mid,lson,a,b);
	if(a>mid)	return query(mid+1,r,rson,a,b);
	return min(query(l,mid,lson,a,b),query(mid+1,r,rson,a,b));
}
ll rd()
{
	ll ret=0;	char gc=getchar();
	while(gc<'0'||gc>'9')	gc=getchar();
	while(gc>='0'&&gc<='9')	ret=ret*10+gc-'0',gc=getchar();
	return ret;
}
void dfs1(int x)
{
	siz[x]=1;
	for(int i=head[x];i!=-1;i=next[i])
	{
		if(to[i]!=fa[x])
		{
			fa[to[i]]=x,dep[to[i]]=dep[x]+1,dfs1(to[i]),siz[x]+=siz[to[i]];
			if(siz[to[i]]>siz[son[x]])	son[x]=to[i];
		}
	}
}
void dfs2(int x,int tp)
{
	top[x]=tp,p[x]=++p[0],Q[p[0]]=x;
	updata(1,n,1,p[0],p[0],v[x]);
	if(son[x])	dfs2(son[x],tp);
	for(int i=head[x];i!=-1;i=next[i])
		if(to[i]!=fa[x]&&to[i]!=son[x])
			dfs2(to[i],to[i]);
	q[x]=p[0];
}
void modify()
{
	int x=rd(),y=rd();
	ll val=rd();
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]])	swap(x,y);
		updata(1,n,1,p[top[x]],p[x],val),x=fa[top[x]];
	}
	if(dep[x]>dep[y])	swap(x,y);
	updata(1,n,1,p[x],p[y],val);
}
void getans()
{
	int x=rd(),y=root,z=root;
	if(x==root)
	{
		printf("%u\n",s[1]);
		return ;
	}
	while(top[y]!=top[x]&&y)	z=top[y],y=fa[top[y]];
	if(dep[x]>dep[y])
	{
		printf("%u\n",query(1,n,1,p[x],q[x]));
		return ;
	}
	if(x!=y)	z=Q[p[x]+1];
	printf("%u\n",min(query(1,n,1,1,p[z]-1),query(1,n,1,q[z]+1,n)));
}
void add(int a,int b)
{
	to[cnt]=b,next[cnt]=head[a],head[a]=cnt++;
}
int main()
{
	n=rd(),m=rd();
	int i,a,b;
	memset(head,-1,sizeof(head));
	for(i=1;i<n;i++)	a=rd(),b=rd(),add(a,b),add(b,a);
	for(i=1;i<=n;i++)	v[i]=rd();
	dep[1]=1,dfs1(1),dfs2(1,1);
	root=rd();
	for(i=1;i<=m;i++)
	{
		a=rd();
		if(a==1)	root=rd();
		if(a==2)	modify();
		if(a==3)	getans();
	}
	return 0;
}

BZOJ3306

#include <cstdio>
#include <cstring>
#include <iostream>
#define lson x<<1
#define rson x<<1|1
using namespace std;
const int maxn=100010;
int n,m,cnt,root;
int to[maxn<<1],next[maxn<<1],head[maxn],dep[maxn],fa[maxn],son[maxn],top[maxn],p[maxn],q[maxn],v[maxn];
int siz[maxn],Q[maxn];
int s[maxn<<2];
char str[maxn];
void updata(int l,int r,int x,int a,int b)
{
	if(l==r)
	{
		s[x]=b;
		return ;
	}
	int mid=l+r>>1;
	if(a<=mid)	updata(l,mid,lson,a,b);
	else	updata(mid+1,r,rson,a,b);
	s[x]=min(s[lson],s[rson]);
}
int query(int l,int r,int x,int a,int b)
{
	if(a>b)	return 0x7fffffff;
	if(a<=l&&r<=b)	return s[x];
	int mid=l+r>>1;
	if(b<=mid)	return query(l,mid,lson,a,b);
	if(a>mid)	return query(mid+1,r,rson,a,b);
	return min(query(l,mid,lson,a,b),query(mid+1,r,rson,a,b));
}
int rd()
{
	int ret=0,f=1;	char gc=getchar();
	while(gc<'0'||gc>'9')	{if(gc=='-')f=-f;	gc=getchar();}
	while(gc>='0'&&gc<='9')	ret=ret*10+gc-'0',gc=getchar();
	return ret*f;
}
void dfs1(int x)
{
	siz[x]=1;
	for(int i=head[x];i!=-1;i=next[i])
	{
		if(to[i]!=fa[x])
		{
			fa[to[i]]=x,dep[to[i]]=dep[x]+1,dfs1(to[i]),siz[x]+=siz[to[i]];
			if(siz[to[i]]>siz[son[x]])	son[x]=to[i];
		}
	}
}
void dfs2(int x,int tp)
{
	top[x]=tp,p[x]=++p[0],Q[p[0]]=x;
	updata(1,n,1,p[0],v[x]);
	if(son[x])	dfs2(son[x],tp);
	for(int i=head[x];i!=-1;i=next[i])
		if(to[i]!=fa[x]&&to[i]!=son[x])
			dfs2(to[i],to[i]);
	q[x]=p[0];
}
void getans()
{
	int x=rd(),y=root,z=root;
	if(x==root)
	{
		printf("%d\n",s[1]);
		return ;
	}
	while(top[y]!=top[x]&&y)	z=top[y],y=fa[top[y]];
	if(dep[x]>dep[y])
	{
		printf("%d\n",query(1,n,1,p[x],q[x]));
		return ;
	}
	if(x!=y)	z=Q[p[x]+1];
	printf("%d\n",min(query(1,n,1,1,p[z]-1),query(1,n,1,q[z]+1,n)));
}
void add(int a,int b)
{
	to[cnt]=b,next[cnt]=head[a],head[a]=cnt++;
}
int main()
{
	n=rd(),m=rd();
	int i,a,b;
	memset(head,-1,sizeof(head));
	for(i=1;i<=n;i++)
	{
		fa[i]=rd(),v[i]=rd();
		if(!fa[i])	root=i;
		else	add(fa[i],i);
	}
	dep[root]=1,dfs1(root),dfs2(root,root);
	for(i=1;i<=m;i++)
	{
		scanf("%s",str);
		if(str[0]=='V')	a=rd(),b=rd(),updata(1,n,1,p[a],b);
		if(str[0]=='E')	root=rd();
		if(str[0]=='Q')	getans();
	}
	return 0;
}