【BZOJ2693】jzptab 莫比乌斯反演

【BZOJ2693】jzptab

Description

Input

一个正整数T表示数据组数

接下来T行 每行两个正整数 表示N、M

Output

T行 每行一个整数 表示第i组数据的结果

Sample Input

1
4 5

Sample Output

122
HINT
T <= 10000
N, M<=10000000

题解：首先用到BZOJ2154的结论

然而这个预处理和询问都是O(n)的，那么我们继续推下去，令D=de

 

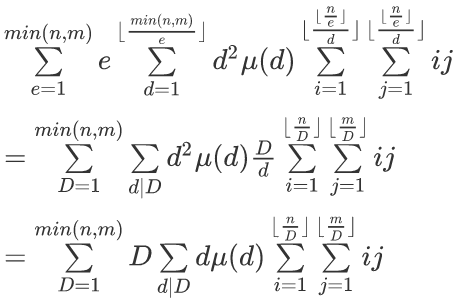
显然∑μ(d)*d是积性函数，可以线性筛出来，设g(i)=∑μ(i)*i

已知i,pri[j]，若i%pri[j]!=0，那么i*pri[j]的所有约数*pri[j]都能得到一个新的约数，并且μ值变成相反数，那么g(i*pri[j])=g(i)-g(i)*pri[j]

若i%pri[j]=0，那么对于i的所有约数*pri[j]得到的数，要么已经是i的约数了，要么μ值=0，所以g(i*pri[j])=g(i)

 

#include <cstdio>
#include <cstring>
#include <iostream>
#define mod 100000009
using namespace std;
const int maxm=10000000;
typedef long long ll;
bool np[maxm+10];
int pri[maxm/10],mu[maxm+10];
ll sm[maxm+10];
int num,T;
int main()
{
	ll i,j,x,y,last,ans;
	sm[1]=mu[1]=1;
	for(i=2;i<=maxm;i++)
	{
		if(!np[i])	pri[++num]=i,mu[i]=-1,sm[i]=-i+1+mod;
		for(j=1;j<=num&&i*pri[j]<=maxm;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				sm[i*pri[j]]=sm[i];
				mu[i*pri[j]]=0;
				break;
			}
			mu[i*pri[j]]=-mu[i];
			sm[i*pri[j]]=(sm[i]-sm[i]*pri[j]%mod+mod)%mod;
		}
	}
	for(i=1;i<=maxm;i++)	sm[i]=(sm[i-1]+sm[i]*i%mod+mod)%mod;
	scanf("%d",&T);
	while(T--)
	{
		scanf("%lld%lld",&x,&y),ans=0;
		if(x<y)	swap(x,y);
		for(i=1;i<=y;i=last+1)
		{
			last=min(x/(x/i),y/(y/i));
			ans=(ans+(sm[last]-sm[i-1]+mod)%mod*((x/i*(x/i+1)>>1)%mod)%mod*((y/i*(y/i+1)>>1)%mod)%mod+mod)%mod;
		}
		printf("%lld\n",ans);
	}
	return 0;
}