【BZOJ2045】双亲数 莫比乌斯反演
【BZOJ2045】双亲数
Description
小D是一名数学爱好者,他对数字的着迷到了疯狂的程度。 我们以d = gcd(a, b)表示a、b的最大公约数,小D执著的认为,这样亲密的关系足可以用双亲来描述,此时,我们称有序数对(a, b)为d的双亲数。 与正常双亲不太相同的是,对于同一个d,他的双亲太多了 >_< 比如,(4, 6), (6, 4), (2, 100)都是2的双亲数。 于是一个这样的问题摆在眼前,对于0 < a <= A, 0 < b <= B,有多少有序数对(a, b)是d的双亲数?
Input
输入文件只有一行,三个正整数A、B、d (d <= A, B),意义如题所示。
Output
输出一行一个整数,给出满足条件的双亲数的个数。
Sample Input
5 5 2
Sample Output
3
【样例解释】
满足条件的三对双亲数为(2, 2) (2, 4) (4, 2)
【样例解释】
满足条件的三对双亲数为(2, 2) (2, 4) (4, 2)
HINT
对于100%的数据满足0 < A, B < 10^ 6
题解: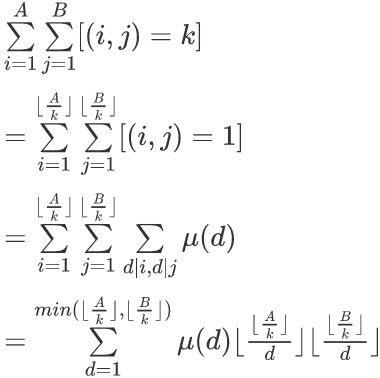
总之就是一旦看到[...=1]就往反演上想就好了
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn=1000010;
int n,m,d,num;
int pri[maxn],mu[maxn],sm[maxn];
bool np[maxn];
typedef long long ll;
ll ans;
int main()
{
scanf("%d%d%d",&n,&m,&d),n/=d,m/=d;
if(n<m) swap(n,m);
int i,j,last;
sm[1]=mu[1]=1;
for(i=2;i<=n;i++)
{
if(!np[i]) pri[++num]=i,mu[i]=-1;
sm[i]=sm[i-1]+mu[i];
for(j=1;j<=num&&i*pri[j]<=n;j++)
{
np[i*pri[j]]=1;
if(i%pri[j]==0)
{
mu[i*pri[j]]=0;
break;
}
mu[i*pri[j]]=-mu[i];
}
}
for(i=1;i<=m;i=last+1)
{
last=min(n/(n/i),m/(m/i));
ans+=1ll*(sm[last]-sm[i-1])*(n/i)*(m/i);
}
printf("%lld",ans);
return 0;
}
| 欢迎来原网站坐坐! >原文链接<


