【BZOJ4176】Lucas的数论 莫比乌斯反演

【BZOJ4176】Lucas的数论

Description

去年的Lucas非常喜欢数论题，但是一年以后的Lucas却不那么喜欢了。

在整理以前的试题时，发现了这样一道题目“求Sigma(f(i)),其中1<=i<=N”，其中 表示i的约数个数。他现在长大了，题目也变难了。

求如下表达式的值：

 

其中 表示ij的约数个数。

他发现答案有点大，只需要输出模1000000007的值。

Input

第一行一个整数n。

Output

 一行一个整数ans，表示答案模1000000007的值。

Sample Input

2

Sample Output

8

HINT

 对于100%的数据n <= 10^9。

题解：前置技能：

然后直接上莫比乌斯反演

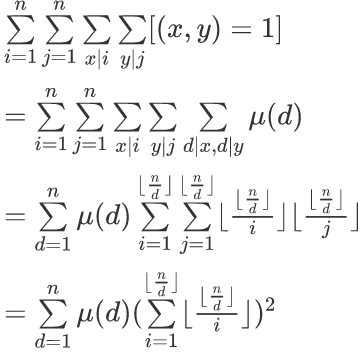
用杜教筛处理μ(d)，然后喜闻乐见的分块~

 

#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#define mod 1000000007
using namespace std;
const int m=10000000;
typedef long long ll;
int n,num;
ll ans;
int mu[m+10],sm[m+10],pri[m+10];
bool np[m+10];
map<ll,ll> mp;
ll getsm(ll x)
{
	if(x<=m)	return sm[x];
	if(mp[x])	return mp[x];
	ll ret=1,i,last;
	for(i=2;i<=x;i=last+1)
	{
		last=x/(x/i);
		ret=(ret-(last-i+1)*getsm(x/i)%mod+mod)%mod;
	}
	mp[x]=ret;
	return ret;
}
ll getf(ll x)
{
	ll ret=0,i,last;
	for(i=1;i<=x;i=last+1)
	{
		last=x/(x/i);
		ret=(ret-(last-i+1)*(x/i)%mod+mod)%mod;
	}
	return ret*ret%mod;
}
int main()
{
	scanf("%d",&n);
	ll i,j,last;
	sm[1]=mu[1]=1;
	for(i=2;i<=m;i++)
	{
		if(!np[i])	pri[++num]=i,mu[i]=-1;
		sm[i]=sm[i-1]+mu[i];
		for(j=1;j<=num&&i*pri[j]<=m;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				mu[i*pri[j]]=0;
				break;
			}
			mu[i*pri[j]]=-mu[i];
		}
	}
	for(i=1;i<=n;i=last+1)
	{
		last=n/(n/i);
		ans=(ans+(getsm(last)-getsm(i-1)+mod)%mod*getf(n/i)%mod)%mod;
	}
	printf("%lld",ans);
	return 0;
}