【BZOJ4916】神犇和蒟蒻 杜教筛

【BZOJ4916】神犇和蒟蒻

Description

很久很久以前，有一只神犇叫yzy;

很久很久之后，有一只蒟蒻叫lty;

Input

请你读入一个整数N;1<=N<=1E9,A、B模1E9+7;

Output

请你输出一个整数A=\sum_{i=1}^N{\mu (i^2)};

请你输出一个整数B=\sum_{i=1}^N{\varphi (i^2)};

Sample Input

1

Sample Output

1
1

题解：哎？上面的那个东西好像一直是1？（废话），然后

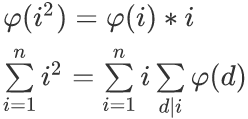
设j=i/d，然后将j提出来

 

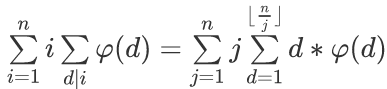
然后就可以用杜教筛了

#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#define mod 1000000007ll
using namespace std;
const int m=3000000;
typedef long long ll;
int n,num;
ll phi[m+10],sp[m+10],pri[m+10];
bool np[m+10];
map<ll,ll>	mp;
ll dfs(ll x)
{
	if(x<=m)	return sp[x];
	if(mp.find(x)!=mp.end())	return mp[x];
	ll rp=x*(x+1)%(mod*6)*(2*x+1)/6%mod,i,last;
	for(i=2;i<=x;i=last+1)
	{
		last=x/(x/i);
		rp=(rp-(last-i+1)*(last+i)/2%mod*dfs(x/i)%mod+mod)%mod;
	}
	mp[x]=rp;
	return rp;
}
int main()
{
	int i,j;
	phi[1]=sp[1]=1;
	for(i=2;i<=m;i++)
	{
		if(!np[i])	pri[++num]=i,phi[i]=i-1;
		sp[i]=(sp[i-1]+phi[i]*i)%mod;
		for(j=1;j<=num&&i*pri[j]<=m;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				phi[i*pri[j]]=phi[i]*pri[j];
				break;
			}
			phi[i*pri[j]]=phi[i]*(pri[j]-1);
		}
	}
	ll a;
	scanf("%lld",&a);
	printf("1\n%lld",dfs(a));
	return 0;
}