线段树笔记

线段树

普通线段树

例 \(1\)

题目描述

给定一个长为 \(n\) 的序列，有 \(m\) 次操作，每次操作为以下三种之一。

  • 修改序列中的一个数
  • 求序列中某连续一段所有数的两两乘积的和 \(\text{mod} 1000000007\)。
  • 求序列中某连续一段所有相邻两数乘积的和 \(\text{mod} 1000000007\)。

做法

一般单点修改的难点都在于区间合并信息的操作。

\(\text{Part}1\)

先考虑第二个操作，假设对于一个区间我们已经求出了它左右两个子区间的两两乘积之和，例如左区间的数为 \(a,b,c\)，我们右区间的数为 \(d,e\)，我们已经知道了 \(a\times b,a\times c,b\times c\) 的和与 \(d \times e\) 的和。

那合并后增加的部分就为 \(a \times d+a\times e+b\times d+b\times e+c\times d+c\times e\) 的和，提取公因式得 \(a\times(d+e)+b\times(d+e)+c\times(d+e)\)，再提取公因式得 \((a+b+c)\times(d+e)\)，我们发现 \(a+b+c\) 与 \(d+e\) 都是维护区间的和，可以在线段树合并时维护区间和就可以了。

具体操作为我们对于每个区间维护两个信息，一个为这个区间的两两元素乘积之和 \(ans_2\)，另一个为这个区间所有元素的和 \(sum\)。

例如在合并 \(A\) 与 \(B\) 区间到 \(C\) 时，可以这么合并：\(C.ans_2=A.ans_2+B.ans_2+A.sum\times B.sum\)，\(C.sum=A.sum+B.sum\)。

\(\text{Part} 2\)

再考虑第一个操作，仿照第二个操作的做法，假设对于一个区间我们已经求出了它左右两个子区间的相邻两数乘积之和，例如左区间的数为 \(a,b,c\)，我们右区间的数为 \(d,e\)，我们已经知道了 \(a\times b,b\times c\) 的和与 \(d \times e\) 的和。

那合并后增加的部分就为 \(c\times d\)，我们发现 \(c\) 与 \(d\) 区间的左右元素，可以在线段树合并时维护左右元素是谁就可以了。

具体操作为我们对于每个区间维护三个信息，一个为这个区间的两两元素乘积之和 \(ans_1\)，另一个为这个区间最左边元素为 \(l\)，最右边元素为 \(r\)。

例如在合并 \(A\) 与 \(B\) 区间到 \(C\) 时，可以这么合并：\(C.ans_1=A.ans_1+B.ans_1+A.r\times B.l\)，\(C.l=A.l,C.r=B.r\)。

这道题启发我们往往不能只维护题目所求的信息（因为这样很有可能无法直接维护）还要维护一些其它的信息。

例 \(2\) 小白逛公园

题目传送门

做法

在例 \(1\) 的引导下，我们可以考虑一个区间的答案可以由左右两个区间的答案更新而来，也可以是左右两个区间的最大子段和，也就是左区间的后缀最大和再加上右区间的前缀最大和。而一个区间的前缀最大和可以是由它的左区间的前缀最大和更新过来，也可使左区间加上右区间的前缀最大和更新过来，右区间同理。所以我们还要维护区间和的信息。

\(Code\)

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+50;
int a[N],n,m;
struct data{
	int sum,leftmax,rightmax,totalmax;
}tree[N*4];
data merge(data A,data B){
	data C;
	C.sum=A.sum+B.sum;
	C.leftmax=max(A.leftmax,A.sum+B.leftmax);
	C.rightmax=max(B.rightmax,B.sum+A.rightmax);
	C.totalmax=max(max(A.totalmax,B.totalmax),A.rightmax+B.leftmax);
	return C;
}
void build(int p,int l,int r){
	if(l==r){
		tree[p].sum=tree[p].leftmax=tree[p].rightmax=tree[p].totalmax=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(p*2,l,mid);build(p*2+1,mid+1,r);
	tree[p]=merge(tree[p*2],tree[p*2+1]);
	return;
}
void modify(int p,int l,int r,int x,int y){
	if(l==r){
		tree[p].sum=y;
		tree[p].leftmax=y;
		tree[p].rightmax=y;
		tree[p].totalmax=y;
		return;
	}
	else{
		int mid=(l+r)/2;
		if(x>mid) modify(p*2+1,mid+1,r,x,y);
		else modify(p*2,l,mid,x,y);
		tree[p]=merge(tree[p*2],tree[p*2+1]);
	}
}
data query(int p,int l,int r,int x,int y){
	if(l>=x&&r<=y){
		return tree[p];
	}
	int mid=(l+r)/2;
	if(y<=mid)return query(p*2,l,mid,x,y);
	else if(x>mid)return query(p*2+1,mid+1,r,x,y);
	else{
		data A=query(p*2,l,mid,x,mid);
		data B=query(p*2+1,mid+1,r,mid+1,y);
		data C;
		
		C.sum=A.sum+B.sum;
		C.leftmax=max(A.leftmax,A.sum+B.leftmax);
		C.rightmax=max(B.rightmax,B.sum+A.rightmax);
		C.totalmax=max(max(A.totalmax,B.totalmax),A.rightmax+B.leftmax);
		return C;
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	build(1,1,n);
	for(int i=1;i<=m;i++){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		if(a==1){
			if(b>c)swap(b,c);
			printf("%d\n",query(1,1,n,b,c).totalmax);
		}
		else{
			modify(1,1,n,b,c);
		}
	}
	return 0;
}

题 \(1\) 【线段树】序列和

题目

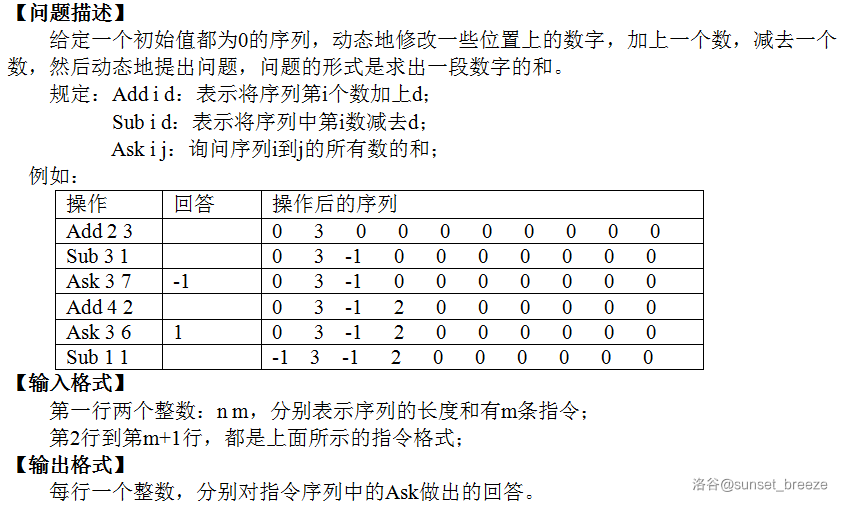
思路

线段树板题，不说了。

\(Code:\)

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 1e5 + 50;
int n,m;
int a[N];
struct Segment
{
	struct node{
		ll sum,tag;
	}T[N * 4];
	void pushup(int p)
	{
		T[p].sum = T[p * 2].sum + T[p * 2 + 1].sum;
		return;
	}
	void build(int p,int l,int r)
	{
		T[p].tag = 0;T[p].sum = 0;
		if(l == r)
		{
			T[p].sum = a[l];
			return;
		}
		int mid = (l + r) >> 1;
		build(p * 2,l,mid);build(p * 2 + 1,mid + 1,r);
		pushup(p);
		return;
	}
	void f(int p,int l,int r,int k)
	{
		T[p].sum += (r - l + 1) * k;
		T[p].tag += k;
		return;
	}
	void pushdown(int p,int l,int r)
	{
		int mid = (l + r) >> 1;
		f(p * 2,l,mid,T[p].tag);f(p * 2 + 1,mid + 1,r,T[p].tag);
		T[p].tag = 0;
		return;
	}
	void update(int p,int l,int r,int x,int y,int k)
	{
		if(x <= l && r <= y)
		{
			T[p].tag += k;
			T[p].sum += (r - l + 1) * k;
			return;
		}
		pushdown(p,l,r);
		int mid = (l + r) >> 1;
		if(x <= mid)update(p * 2,l,mid,x,y,k);
		if(y > mid)update(p * 2 + 1,mid + 1,r,x,y,k);
		pushup(p);
		return;
	}
	ll query(int p,int l,int r,int x,int y)
	{
		if(x <= l && r <= y)
			return T[p].sum;
		pushdown(p,l,r);
		int mid = (l + r) >> 1;
		ll res = 0;
		if(x <= mid)res += query(p * 2,l,mid,x,y);
		if(y > mid)res += query(p * 2 + 1,mid + 1,r,x,y);
		return res;
	}
}
T;
int main()
{
	scanf("%d %d",&n,&m);
	T.build(1,1,n);
	while(m--)
	{
		getchar();
		char op[3];
		scanf("%s",op);
		if(op[0] == 'A' && op[1]=='s')
		{
			int x,y,k;
			scanf("%d %d",&x,&y);
			printf("%lld\n",T.query(1,1,n,x,y));
		}
		else
		{
			int x,y;
			scanf("%d %d",&x,&y);
			if(op[0]=='S')y=-y;
			T.update(1,1,n,x,x,y);
		}
	}
	return 0;
}

题 \(2\) 【线段树】简单题（CQOI2006）

思路

区间翻转，考虑为护 \(tag\)，表示一个区间被翻转几次。查询时直接下传标记即可。

\(Code:\)

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 1e5 + 50;
int n,m;
int a[N];
struct Segment
{
	struct node{
		int len,sum,lmax1,rmax1,max1,lmax0,rmax0,max0;
		bool tag,tag1,tag2;
	}T[N * 4];
	void pushup(int p)
	{
		T[p].sum = T[p * 2].sum + T[p * 2 + 1].sum;
		T[p].max1 = max(T[p * 2].max1,T[p * 2 + 1].max1);
		T[p].max1 = max(T[p].max1,T[p * 2].rmax1 + T[p * 2 + 1].lmax1);
		T[p].max0 = max(T[p * 2].max0,T[p * 2 + 1].max0);
		T[p].max0 = max(T[p].max0,T[p * 2].rmax0 + T[p * 2 + 1].lmax0);
		if(T[p * 2].rmax1 == T[p * 2].len)T[p].max1 = max(T[p].max1,T[p * 2].len + T[p * 2 + 1].lmax1);
		if(T[p * 2 + 1].lmax1 == T[p * 2 + 1].len)T[p].max1 = max(T[p].max1,T[p * 2 + 1].len + T[p * 2].rmax1);
		if(T[p * 2].rmax0 == T[p * 2].len)T[p].max0 = max(T[p].max0,T[p * 2].len + T[p * 2 + 1].lmax0);
		if(T[p * 2 + 1].lmax0 == T[p * 2 + 1].len)T[p].max0 = max(T[p].max0,T[p * 2 + 1].len + T[p * 2].rmax0);
		T[p].lmax1 = T[p * 2].lmax1;T[p].lmax0 = T[p * 2].lmax0;
		T[p].rmax1 = T[p * 2 + 1].rmax1;T[p].rmax0 = T[p * 2 + 1].rmax0;
		if(T[p * 2].lmax1 == T[p * 2].len)T[p].lmax1 = max(T[p].lmax1,T[p * 2].len + T[p * 2 + 1].lmax1);
		if(T[p * 2].lmax0 == T[p * 2].len)T[p].lmax0 = max(T[p].lmax0,T[p * 2].len + T[p * 2 + 1].lmax0);
		if(T[p * 2 + 1].rmax1 == T[p * 2 + 1].len)T[p].rmax1 = max(T[p].rmax1,T[p * 2 + 1].len + T[p * 2].rmax1);
		if(T[p * 2 + 1].rmax0 == T[p * 2 + 1].len)T[p].rmax0 = max(T[p].rmax0,T[p * 2 + 1].len + T[p * 2].rmax0);
		return;
	}
	void build(int p,int l,int r)
	{
		T[p].tag = 0;T[p].sum = 0;T[p].len = r - l + 1;T[p].max1 = 0;T[p].tag = T[p].tag1 = T[p].tag2 = 0;
		T[p].lmax1 = T[p].rmax1 = 0;
		if(l == r)
		{
			if(a[l] == 1)
				T[p].max1 = T[p].lmax1 = T[p].rmax1 = T[p].sum = 1;
			if(a[l] == 0)
				T[p].max0 = T[p].lmax0 = T[p].rmax0 = 1;
			return;
		}
		int mid = (l + r) >> 1;
		build(p * 2,l,mid);build(p * 2 + 1,mid + 1,r);
		pushup(p);
		return;
	}
	void f(int p,int l,int r)
	{
		T[p].sum = T[p].len - T[p].sum;
		swap(T[p].lmax1,T[p].lmax0);swap(T[p].rmax1,T[p].rmax0);swap(T[p].max1,T[p].max0);
		if(T[p].tag1 || T[p].tag2)
			swap(T[p].tag1,T[p].tag2);
		else
			T[p].tag ^= 1;
		return;
	}
	void pushdown(int p,int l,int r)
	{
		int mid = (l + r) >> 1;
		f(p * 2,l,mid);f(p * 2 + 1,mid + 1,r);
		T[p].tag = 0;
		return;
	}
	void f1(int p,int l,int r)
	{
		T[p].tag = 0;T[p].tag2 = 0;
		T[p].max1 = T[p].lmax1 = T[p].rmax1 = T[p].sum = 0;
		T[p].max0 = T[p].lmax0 = T[p].rmax0 = T[p].len;
		T[p].tag1 = 1;
		return;
	}
	void pushdown1(int p,int l,int r)
	{
		int mid = (l + r) >> 1;
		f1(p * 2,l,mid);f1(p * 2 + 1,mid + 1,r);
		T[p].tag1 = 0;
		return;
	}
	void f2(int p,int l,int r)
	{
		T[p].tag = 0;T[p].tag1 = 0;
		T[p].max1 = T[p].lmax1 = T[p].rmax1 = T[p].sum = T[p].len;
		T[p].max0 = T[p].lmax0 = T[p].rmax0 = 0;
		T[p].tag2 = 1;
		return;
	}
	void pushdown2(int p,int l,int r)
	{
		int mid = (l + r) >> 1;
		f2(p * 2,l,mid);f2(p * 2 + 1,mid + 1,r);
		T[p].tag2 = 0;
		return;
	}
	void update(int p,int l,int r,int x,int y,int op)
	{
//		cout << l << " " << r << " " << x << " " << y <<endl;
		if(x <= l && r <= y)
		{
			if(op == 2)
				f(p,l,r);
			else if(op == 0)
			{
				T[p].tag = 0;T[p].tag2 = 0;
				T[p].max1 = T[p].lmax1 = T[p].rmax1 = T[p].sum = 0;
				T[p].max0 = T[p].lmax0 = T[p].rmax0 = T[p].len;
				T[p].tag1 = 1;
			}
			else if(op == 1)
			{
				T[p].tag = 0;T[p].tag1 = 0;
				T[p].max1 = T[p].lmax1 = T[p].rmax1 = T[p].sum = T[p].len;
				T[p].max0 = T[p].lmax0 = T[p].rmax0 = 0;
				T[p].tag2 = 1;
			}
			return;
		}
		if(T[p].tag)
			pushdown(p,l,r);
		if(T[p].tag1)
			pushdown1(p,l,r);
		if(T[p].tag2)
			pushdown2(p,l,r);
		int mid = (l + r) >> 1;
		if(x <= mid)update(p * 2,l,mid,x,y,op);
		if(y > mid)update(p * 2 + 1,mid + 1,r,x,y,op);
		pushup(p);
		return;
	}
	int query1(int p,int l,int r,int x,int y)
	{
//		cout << l << " " << r << " " << x << " " << y << " " << T[p].sum << " " <<T[p].tag1 << " " << T[p].tag2 << endl;
		if(x <= l && r <= y)
			return T[p].sum;
		if(T[p].tag)
			pushdown(p,l,r);
		if(T[p].tag1)
			pushdown1(p,l,r);
		if(T[p].tag2)
			pushdown2(p,l,r);
		int mid = (l + r) >> 1;
		int res = 0;
		if(x <= mid)res += query1(p * 2,l,mid,x,y);
		if(y > mid)res += query1(p * 2 + 1,mid + 1,r,x,y);
		return res;
	}
	node query2(int p,int l,int r,int x,int y)
	{
//		cout << l << " " << r << " " << x << " " << y <<endl;
		if(x <= l && r <= y)
			return T[p];
		if(T[p].tag)
			pushdown(p,l,r);
		if(T[p].tag1)
			pushdown1(p,l,r);
		if(T[p].tag2)
			pushdown2(p,l,r);
		int mid = (l + r) >> 1;
		if(x <= mid && y <= mid)
			return query2(p * 2,l,mid,x,y);
		if(y > mid && x > mid)
			return query2(p * 2 + 1,mid + 1,r,x,y);
		else
		{
			node res;
			res.rmax1 = res.lmax1 = res.max1 = 0;
			res.rmax0 = res.lmax0 = res.max0 = 0;
			node res1 = query2(p * 2,l,mid,x,y);
			node res2 = query2(p * 2 + 1,mid + 1,r,x,y);
			res.len = res1.len + res2.len;
			res.max1 = max(res.max1,max(res1.max1,res2.max1));
			res.max1 = max(res.max1,res1.rmax1 + res2.lmax1);
			if(res1.rmax1 == res1.len)res.max1 = max(res.max1,res1.len + res2.lmax1);
			if(res2.lmax1 == res2.len)res.max1 = max(res.max1,res2.len + res1.rmax1);
			res.lmax1 = res1.lmax1;res.lmax0 = res1.lmax0;
			res.rmax1 = res2.rmax1;res.rmax0 = res2.rmax0;
			if(res1.lmax1 == res1.len)res.lmax1 = max(res.lmax1,res1.len + res2.lmax1);
			if(res1.lmax0 == res1.len)res.lmax0 = max(res.lmax0,res1.len + res2.lmax0);
			if(res2.rmax1 == res2.len)res.rmax1 = max(res.rmax1,res2.len + res1.rmax1);
			if(res2.rmax0 == res2.len)res.rmax0 = max(res.rmax0,res2.len + res1.rmax0);
			return res;
		}
	}
}
T;
int main()
{
	scanf("%d %d",&n,&m);
	T.build(1,1,n);
	while(m--)
	{
		int op,a,b;
		scanf("%d",&op);
		if(op == 1)
		{
			scanf("%d %d",&a,&b);
			T.update(1,1,n,a,b,2);
		}
		else
		{
			scanf("%d",&a);
			int x=T.query1(1,1,n,a,a);
			printf("%d\n",x);
		}
	}
	return 0;
}

题 \(3\) 【线段树】线段统计

题目

在数轴上进行一系列操作。每次操作有两种类型，一种是在线段[a,b]上涂上颜色，另一种将[a,b]上的颜色擦去。问经过一系列的操作后，有多少条单位线段[k,k+1]被涂上了颜色。

思路

就是一个区间赋值为 \(1\) 和 \(0\) 的两种操作。最后查询时直接返回整个数列的和即可。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
const int N=6e4+50;
int n,m,a[N];
struct Segment
{
	struct node{
		int sum,tag;
	}T[N * 4];
	void pushup(int p)
	{
		T[p].sum = T[p * 2].sum + T[p * 2 + 1].sum;
		return;
	}
	void build(int p,int l,int r)
	{
		T[p].tag = -1;T[p].sum = 0;
		if(l == r)
		{
			T[p].sum = a[l];
			return;
		}
		int mid = (l + r) >> 1;
		build(p * 2,l,mid);build(p * 2 + 1,mid + 1,r);
		pushup(p);
		return;
	}
	void f(int p,int l,int r,int k)
	{
		T[p].sum = (r - l + 1) * k;
		T[p].tag = k;
		return;
	}
	void pushdown(int p,int l,int r)
	{
		int mid = (l + r) >> 1;
		f(p * 2,l,mid,T[p].tag);f(p * 2 + 1,mid + 1,r,T[p].tag);
		T[p].tag = -1;
		return;
	}
	void update(int p,int l,int r,int x,int y,int k)
	{
		if(x <= l && r <= y)
		{
			T[p].tag=k;
			T[p].sum=(r-l+1)*k;
			return;
		}
		if(T[p].tag!=-1)pushdown(p,l,r);
		int mid = (l + r) >> 1;
		if(x <= mid)update(p * 2,l,mid,x,y,k);
		if(y > mid)update(p * 2 + 1,mid + 1,r,x,y,k);
		pushup(p);
		return;
	}
	int query(int p,int l,int r,int x,int y)
	{
		if(x <= l && r <= y)
			return T[p].sum;
		if(T[p].tag!=-1)pushdown(p,l,r);
		int mid = (l + r) >> 1;
		int res = 0;
		if(x <= mid)res += query(p * 2,l,mid,x,y);
		if(y > mid)res += query(p * 2 + 1,mid + 1,r,x,y);
		return res;
	}
}
T;
int main()
{
	scanf("%d %d",&n,&m);
	T.build(1,1,n);
	for(int i=1;i<=m;i++)
	{
		int op,l,r;
		scanf("%d %d %d",&op,&l,&r);
		if(op==1)T.update(1,1,n,l,r-1,1);
		else T.update(1,1,n,l,r-1,0);
	}
	printf("%d\n",T.query(1,1,n,1,n));
	return 0;
}

题 \(4\) 【线段树】售票系统

题目

某次列车经C个城市，城市编号依次为1到C，列车上共有S个座位，铁路局规定售出的车票只能是坐票，即车上所有的旅客都有座。售票系统是由计算机执行的，每一个售票申请包含三个参数，分别用O,D,N表示，O为起始，D为目的地站，N为车票张数。售票系统对该售票申请作出受理和不受理的决定，只有在从O到D的区段内列车上都有N个和N个以上的空座位时该售票申请才被受理。

　　请你写一个程序，实现这个自动售票系统。

思路

题意可转化为：

  • 修改：将一个区间整体加上一个数，并更新最值，注意这里的一个点 \(i\) 表示 原序列的 \([i,i+1]\)。

  • 查询：统计一个区间的最大值是否大于一个值，如果没有这个区间就加上这个值，否则跳过。

通过分析我们要快速修改与询问区间的最值，注意到这些信息都可以合并也就是可以 \(pushup\) ，所以我们可以考虑用线段树解决此题。

\(Code:\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e4+50;
int n,s,m;
struct SegmentTree{
	struct node{
		int tag,maxx;
	}T[N*4];
	void pushup(int p)
	{
		T[p].maxx=max(T[p*2].maxx,T[p*2+1].maxx);
		return;
	}
	void build(int p,int l,int r)
	{
		T[p].tag=T[p].maxx=0;
		if(l==r)
		{
			T[p].maxx=0;
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		pushup(p);
		return;
	}
	void pushdown(int p)
	{
		T[p*2].tag+=T[p].tag;
		T[p*2+1].tag+=T[p].tag;
		T[p*2].maxx+=T[p].tag;
		T[p*2+1].maxx+=T[p].tag;
		T[p].tag=0;
		return;
	}
	void update(int p,int l,int r,int x,int y,int k)
	{
		if(x<=l&&r<=y)
		{
			T[p].maxx+=k;
			T[p].tag+=k;
			return;
		}
		if(T[p].tag!=0)pushdown(p);
		int mid=(l+r)>>1;
		if(x<=mid)update(p*2,l,mid,x,y,k);
		if(y>mid)update(p*2+1,mid+1,r,x,y,k);
		pushup(p);
		return;
	}
	int query(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
			return T[p].maxx;
		if(T[p].tag!=0)pushdown(p);
		int mid=(l+r)>>1,res=0;
		if(x<=mid)res=max(res,query(p*2,l,mid,x,y));
		if(y>mid)res=max(res,query(p*2+1,mid+1,r,x,y));
		return res;
	}
}T;
signed main()
{
	scanf("%lld %lld %lld",&n,&s,&m);
	T.build(1,1,n);
	for(int i=1;i<=m;i++)
	{
		int l,r,x;
		scanf("%lld %lld %lld",&l,&r,&x);
		if(T.query(1,1,n,l,r-1)+x<=s)
		{
			T.update(1,1,n,l,r-1,x);
			printf("YES\n");
		}
		else printf("NO\n");
	}
	return 0;
}

题 \(5\) 【线段树】影子的宽度

题目

桌子上零散地放着若干个盒子，盒子都平行于墙。桌子的后方是一堵墙。如图所示。现在从桌子的前方射来一束平行光，把盒子的影子投射到了墙上。问影子的总宽度是多少？

思路

题意可转化为：

  • 修改：将一个区间整体赋值为 \(1\)，并更新区间和，注意这里的一个点 \(i\) 表示 原序列的 \([i,i+1]\)。

  • 查询：统计区间和。

通过分析我们要快速修改与询问区间和，典型的线段树，但是注意要加上偏移量，避免下标出现负数。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+60,M=1e5+10;
int xc,n;
struct SegmentTree{
	struct node{
		int ans,tag;
	}T[N*4];
	node merge(node A,node B)
	{
		node C;
		C.tag=-1;C.ans=A.ans+B.ans;
		return C; 
	}
	void pushup(int p)
	{
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	void build(int p,int l,int r)
	{
		T[p].tag=-1;
		if(l==r)
		{
			T[p].ans=0;
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		pushup(p);
		return;
	}
	void f(int p,int l,int r)
	{
		T[p].tag=1;T[p].ans=r-l+1;
		return;
	}
	void pushdown(int p,int l,int r)
	{
		int mid=(l+r)>>1;
		f(p*2,l,mid);f(p*2+1,mid+1,r);
		T[p].tag=0;
		return;
	}
	void update(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
		{
			T[p].ans=r-l+1;
			T[p].tag=1;
			return;
		}
		if(T[p].tag==1)
			pushdown(p,l,r);
		int mid=(l+r)>>1;
		if(x<=mid)update(p*2,l,mid,x,y);
		if(y>mid)update(p*2+1,mid+1,r,x,y);
		pushup(p);
		return;
	}
}T;
int L,R;
int main()
{
	scanf("%d %d %d",&L,&R,&n);
	L+=M;R+=M; 
	T.build(1,1,200050);
	for(int i=1;i<=n;i++)
	{
		int l,r;
		scanf("%d %d",&l,&r);
		l+=M;r+=M;
		T.update(1,1,200050,l,r-1);
	}
	printf("%d\n",T.T[1].ans);
	return 0;
}

题 \(6\) 【线段树】盒子的个数

题目

桌子上零散地按照后先后顺序放着若干个盒子，盒子都平行于墙。桌子的后方是一堵墙。如图所示。问从桌子前方可以看到多少个盒子？假设人站得足够远。（注意，只能看到墙范围内的盒子）

思路

考虑到后面插入的线段更不容易被覆盖，所以从后往前处理，依次插入线段，如果这个线段没有被完全覆盖，那么 \(ans+1\)，并覆盖剩余区间，否则就跳过。

\(Code:\)

#include <bits/stdc++.h>
#define int long long
#define maxm 2000005
#define maxn 1005
#define uni 100005
#define inf 0x3f3f3f3fa
using namespace std;
int t,ll,rr,n,w,sum,ans;
int x[maxm],y[maxm];
bool flag;
#define lc 2*k
#define rc 2*k+1
struct Seg{
	int l,r,flag;
}tree[maxm];
void Build(int k,int l,int r){
	tree[k]=(Seg){l,r,0};
	if(l==r)return ;
	int mid=(l+r)>>1;
	Build(lc,l,mid);
	Build(rc,mid+1,r);
}
void pushup(int k){
	if(tree[lc].flag&&tree[rc].flag)tree[k].flag=1;
}
void pushdown(int k){
	if(!tree[k].flag)return;
	tree[lc].flag=tree[rc].flag=1;
}
void Ask(int k,int l,int r){
	if(tree[k].l>r||tree[k].r<l)return ;
	if(tree[k].l>=l&&tree[k].r<=r){
		if(tree[k].flag==0){
			flag=true;
			tree[k].flag=1;
		}
		return;
	}
	pushdown(k);
	Ask(lc,l,r);
	Ask(rc,l,r);
	pushup(k);
}
signed main(){
	cin>>ll>>rr>>n;
	ll+=uni;
	rr+=uni;
	rr--; 
	Build(1,ll,rr);
	for(int i=1;i<=n;i++)cin>>x[i]>>y[i];
	for(int i=n;i>=1;i--){
		flag=false;
		Ask(1,x[i]+uni,y[i]+uni-1);
		if(flag==true)ans++;
	}
	cout<<ans;
	
    return 0;
}

题 \(7\) 【线段树】线段颜色条数

题目

X轴上从下向上依次叠放一定长度的某种颜色的线段。问从上向下看X轴，它被分成了不同颜色的多少段？

思路

乍眼一看分块or莫队模板题？但是看到只有一次询问，就可以直接上线段树了，直接暴力模拟即可。统计每个线段树区间的左右端点所处的颜色连续块的颜色。进行合并即可。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+60,M=1e5+50;
int xc,n;
struct SegmentTree{
	struct node{
		int lc,rc,ans,tag;
	}T[N*4];
	node merge(node A,node B)
	{
		node C;C.lc=C.rc=C.ans=0;C.tag=-1;
		if(A.rc==B.lc)C.ans=A.ans+B.ans-1;
		else C.ans=A.ans+B.ans;
		C.lc=A.lc;C.rc=B.rc;
		return C; 
	}
	void pushup(int p)
	{
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	void build(int p,int l,int r)
	{
		T[p].tag=-1;T[p].lc=T[p].rc=T[p].ans=0;
		if(l==r)
		{
			T[p].lc=T[p].rc=xc;T[p].ans=1;
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		pushup(p);
		return;
	}
	void f(int p,int k)
	{
		T[p].tag=k;
		T[p].ans=1;T[p].lc=T[p].rc=k;
		return;
	}
	void pushdown(int p)
	{
		f(p*2,T[p].tag);f(p*2+1,T[p].tag);
		T[p].tag=-1;
		return;
	}
	void update(int p,int l,int r,int x,int y,int k)
	{
		if(x<=l&&r<=y)
		{
			T[p].ans=1;T[p].lc=T[p].rc=k;
			T[p].tag=k;
			return;
		}
		if(T[p].tag!=-1)
			pushdown(p);
		int mid=(l+r)>>1;
		if(x<=mid)update(p*2,l,mid,x,y,k);
		if(y>mid)update(p*2+1,mid+1,r,x,y,k);
		pushup(p);
		return;
	}
}T;
int main()
{
	scanf("%d %d",&xc,&n);
	T.build(1,1,200010);
	for(int i=1;i<=n;i++)
	{
		int l,r,x;
		scanf("%d %d %d",&l,&r,&x);
		l+=M;r+=M;
		T.update(1,1,200010,l,r-1,x);
	}
	cout<<T.T[1].ans<<endl;
	return 0;
}

题 \(8\) 【线段树】线段的条数

题目

X轴上从下向上依次叠放一定长度某种颜色的线段。问在某个单位区间上一共叠放了多少条线段？

思路

好像不用线段树更简单？因为只有一次询问，直接 \(O(n)\) 暴力枚举即可。这提示我们有时候不要一看到题就开始想复杂的解法，而是要看完整个题目后彻底思考后再设计算法解决。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+50;
int h,n,m;
int l[N],r[N];
int main()
{
	scanf("%d %d",&h,&n);
	for(int i=1,x;i<=n;i++)
		scanf("%d %d %d",&l[i],&r[i],&x);
	scanf("%d",&m);
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		if(l[i]<=m&&r[i]>=m+1)
			ans++;
	}
	printf("%d\n",ans);
	return 0; 
}

题 \(9\) GSS1 - Can you answer these queries I

思路

这就是一个求区间最大子段和模板题。直接上线段树就行了。维护一个节点的 \(ans\)（表示区间内的答案），\(lans\) 表示以左端点开始的最大子段和，\(rans\) 表示以右端点开始的最大子段和。

\(pushup\) 操作即为

node merge(node A,node B)
{
	node C;C.lans=C.rans=C.ans=C.sum=0;
	C.ans=max(A.ans,B.ans);C.lans=A.lans;C.rans=B.rans;C.sum=A.sum+B.sum;
	C.ans=max(C.ans,A.rans+B.lans);
	C.lans=max(C.lans,A.sum+B.lans);C.rans=max(C.rans,A.rans+B.sum);
	return C;
}

结合代码还是很好理解的。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e4+50;
int n,m;
int a[N];
struct SegmentTree{
	struct node{
		int lans,rans,ans,sum;
	}T[N*4];
	node merge(node A,node B)
	{
		node C;C.lans=C.rans=C.ans=C.sum=0;
		C.ans=max(A.ans,B.ans);C.lans=A.lans;C.rans=B.rans;C.sum=A.sum+B.sum;
		C.ans=max(C.ans,A.rans+B.lans);
		C.lans=max(C.lans,A.sum+B.lans);C.rans=max(C.rans,A.rans+B.sum);
		return C;
	}
	void build(int p,int l,int r)
	{
		T[p].lans=T[p].rans=T[p].ans=T[p].sum=0;
		if(l==r)
		{
			T[p].sum=T[p].lans=T[p].rans=T[p].ans=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	void update(int p,int l,int r,int x,int y)
	{
		if(l==r)
		{
			T[p].ans=T[p].lans=T[p].rans=T[p].sum=y;
			return;
		}
		int mid=(l+r)>>1;
		if(x<=mid)update(p*2,l,mid,x,y);
		else update(p*2+1,mid+1,r,x,y);
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	node query(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
			return T[p];
		int mid=(l+r)>>1;
		if(x<=mid&&y<=mid)return query(p*2,l,mid,x,y);
		else if(x>mid&&y>mid)return query(p*2+1,mid+1,r,x,y);
		else return merge(query(p*2,l,mid,x,y),query(p*2+1,mid+1,r,x,y));
	}
}T;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	T.build(1,1,n);
	scanf("%d",&m);
	while(m--)
	{
		int x,y;
		scanf("%d %d",&x,&y);
		printf("%d\n",T.query(1,1,n,x,y).ans);
	}
	return 0;
}

题 \(10\) GSS3 - Can you answer these queries III

思路

题意就是要求带单点修改的区间最大子段和，还是直接线段树。

具体实现看上一道题即可。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e4+50;
int n,m;
int a[N];
struct SegmentTree{
	struct node{
		int lans,rans,ans,sum;
	}T[N*4];
	node merge(node A,node B)
	{
		node C;C.lans=C.rans=C.ans=C.sum=0;
		C.ans=max(A.ans,B.ans);C.lans=A.lans;C.rans=B.rans;C.sum=A.sum+B.sum;
		C.ans=max(C.ans,A.rans+B.lans);
		C.lans=max(C.lans,A.sum+B.lans);C.rans=max(C.rans,A.rans+B.sum);
		return C;
	}
	void build(int p,int l,int r)
	{
		T[p].lans=T[p].rans=T[p].ans=T[p].sum=0;
		if(l==r)
		{
			T[p].sum=T[p].lans=T[p].rans=T[p].ans=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	void update(int p,int l,int r,int x,int y)
	{
		if(l==r)
		{
			T[p].ans=T[p].lans=T[p].rans=T[p].sum=y;
			return;
		}
		int mid=(l+r)>>1;
		if(x<=mid)update(p*2,l,mid,x,y);
		else update(p*2+1,mid+1,r,x,y);
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	node query(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
			return T[p];
		int mid=(l+r)>>1;
		if(x<=mid&&y<=mid)return query(p*2,l,mid,x,y);
		else if(x>mid&&y>mid)return query(p*2+1,mid+1,r,x,y);
		else return merge(query(p*2,l,mid,x,y),query(p*2+1,mid+1,r,x,y));
	}
}T;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	T.build(1,1,n);
	scanf("%d",&m);
	while(m--)
	{
		int op,x,y;
		scanf("%d %d %d",&op,&x,&y);
		if(op==1)
		{
			if(x>y)swap(x,y);
			printf("%d\n",T.query(1,1,n,x,y).ans);
		}
		else T.update(1,1,n,x,y);
	}
	return 0;
}

题 \(11\) 【线段树】最大子段和

思路

和上一道题一模一样。

#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef long long ll;
const int N=5e5+50;
int n,m;
int a[N];
struct SegmentTree{
	struct node{
		int lans,rans,ans,sum;
	}T[N*4];
	node merge(node A,node B)
	{
		node C;C.lans=C.rans=C.ans=C.sum=0;
		C.ans=max(A.ans,B.ans);C.lans=A.lans;C.rans=B.rans;C.sum=A.sum+B.sum;
		C.ans=max(C.ans,A.rans+B.lans);
		C.lans=max(C.lans,A.sum+B.lans);C.rans=max(C.rans,A.rans+B.sum);
		return C;
	}
	void build(int p,int l,int r)
	{
		T[p].lans=T[p].rans=T[p].ans=T[p].sum=0;
		if(l==r)
		{
			T[p].sum=T[p].lans=T[p].rans=T[p].ans=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	void update(int p,int l,int r,int x,int y)
	{
		if(l==r)
		{
			T[p].ans=T[p].lans=T[p].rans=T[p].sum=y;
			return;
		}
		int mid=(l+r)>>1;
		if(x<=mid)update(p*2,l,mid,x,y);
		else update(p*2+1,mid+1,r,x,y);
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	node query(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
			return T[p];
		int mid=(l+r)>>1;
		if(x<=mid&&y<=mid)return query(p*2,l,mid,x,y);
		else if(x>mid&&y>mid)return query(p*2+1,mid+1,r,x,y);
		else return merge(query(p*2,l,mid,x,y),query(p*2+1,mid+1,r,x,y));
	}
}T;
signed main()
{
	scanf("%lld %lld",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%lld",&a[i]);
	T.build(1,1,n);
	while(m--)
	{
		int op,x,y;
		scanf("%lld %lld %lld",&op,&x,&y);
		if(op==1)
		{
			if(x>y)swap(x,y);
			printf("%lld\n",T.query(1,1,n,x,y).ans);
		}
		else T.update(1,1,n,x,y);
	}
	return 0;
}

题 \(12\) GSS5 - Can you answer these queries V

思路

  • 先考虑两个区间不重合的情况：直接求出 \([y1,x2]\) 的和再加上 \([l,y1-1] ~~(l \in [x,y1-1])\) 的后缀最大和与 \([x2+1,r]~~(r \in [x2+1,y2])\) 的前缀最大和。最后相加求和即可，用线段树+前缀和维护即可。
  • 再考虑两个区间重合的情况：我们可以考虑成三部分：\([x1,x2],[x2,y1],[y1,y2]\)。只有一种情况起点和终点在三个区间的同一个区间中，就是 \([x2,y1]\) 中所以直接用线段树求出最大子段和即可。还有就是不在同一个区间时有以下几种情况：\(x \in [x1,x2],y \in [x2,y1]\)，\(x \in [x1,x2],y \in[y1,y2]\)，\(x \in [x2,y1],y \in [y1,y2]\)。直接用线段树维护即可。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+50;
int cas;
int n,a[N],m;
struct SegmentTree{
	struct node{
		int lans,rans,sum,ans;
	}T[N*4];
	node merge(node A,node B)
	{
		node C;C.lans=C.rans=C.sum=C.ans=0;
		C.sum=A.sum+B.sum;
		C.ans=max(A.ans,B.ans);C.ans=max(C.ans,A.rans+B.lans);
		C.lans=A.lans;C.lans=max(C.lans,A.sum+B.lans);
		C.rans=B.rans;C.rans=max(C.rans,A.rans+B.sum);
		return C; 
	}
	void pushup(int p)
	{
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	void build(int p,int l,int r)
	{
		T[p].ans=T[p].lans=T[p].rans=T[p].sum=0;
		if(l==r)
		{
			T[p].lans=T[p].rans=T[p].ans=T[p].sum=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		pushup(p);
		return;
	}
	node query(int p,int l,int r,int x,int y)
	{
		if(x>y)
			return node{0,0,0,0};
		if(x<=l&&r<=y)
			return T[p];
		int mid=(l+r)>>1;
		if(x<=mid&&y<=mid)return query(p*2,l,mid,x,y);
		else if(x>mid&&y>mid)return query(p*2+1,mid+1,r,x,y);
		else return merge(query(p*2,l,mid,x,y),query(p*2+1,mid+1,r,x,y));
	}
}T;
int main()
{
//	freopen("data.in","r",stdin);
//	freopen("baoli.out","w",stdout);
	scanf("%d",&cas);
	while(cas--)
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			scanf("%d",&a[i]);
		T.build(1,1,n);
		scanf("%d",&m);
		while(m--)
		{
			int a1,b1,a2,b2;
			scanf("%d %d %d %d",&a1,&b1,&a2,&b2);
			if(b1>=a2)
			{
				int x=T.query(1,1,n,a2,b1).ans;
//				cout<<x<<endl;
//				cout<<T.query(1,1,n,a2,b1).sum<<" "<<T.query(1,1,n,a1,a2-1).rans<<" "<<T.query(1,1,n,b1+1,b2).lans<<endl<<endl;
				x=max(x,T.query(1,1,n,a2,b1).sum+max(0,T.query(1,1,n,a1,a2-1).rans)+max(0,T.query(1,1,n,b1+1,b2).lans));
				x=max(x,T.query(1,1,n,a1,a2-1).rans+T.query(1,1,n,a2,b1).lans);
				x=max(x,T.query(1,1,n,a2,b1).rans+T.query(1,1,n,b1+1,b2).lans);
				printf("%d\n",x);
			}
			else
				printf("%d\n",T.query(1,1,n,b1,a2).sum+max(0,T.query(1,1,n,a1,b1-1).rans)+max(0,T.query(1,1,n,a2+1,b2).lans));
		}
	}
	return 0;
}

题 \(13\) 【线段树】最大连续和（POJ2750）

题目

给出一个含有N个结点的环，编号分别为1..N，环上的点带有权值（可正可负），现要动态的修改某个点的权值，求每次修改后环上的最大连续和，但不能是整个序列的和。

思路

环上问题一般有两种思考方向：

  • 破环为链，直接二倍倍长数组即可。但放这道题上明显不是很好做。因为要枚举左端点，一共要枚举 \(n\) 次，且每次枚举时间复杂度为 \(O(log_n)\)，一共 \(Q\) 次修改所以总时间复杂度为 \(O(Q\times nlog_n)\)，T到家了。
  • 但还有一种不是很常见的环问题处理方式，就是直接暴力在原数组上维护即可。

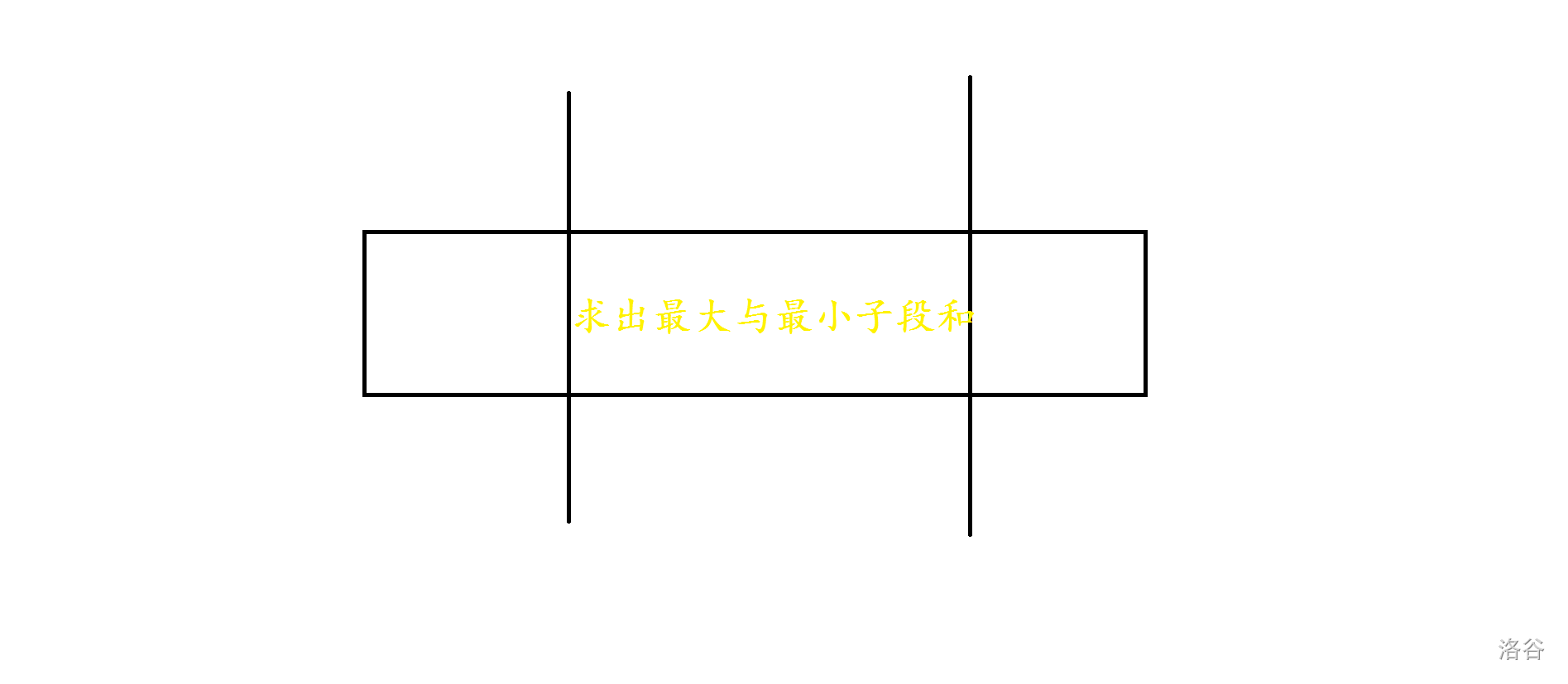
考虑到是在环上选取最大子段和区间，那么可以分两种情况：

  • 答案区间被完全连续包含在原定数组上，那么直接求出线段树维护带单点修该+区间查询最大子段和即可。
  • 否则，答案不被连续包含在原定数组上，答案区间一定是原数组的前缀的一部分和后缀的一部分，那么加起来为最大值的条件即为原数组所有元素的和再减去原数组的最小子段和，用线段树维护即可。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+50;
int n,q;
int a[N];
struct SegmentTree{
	struct node{
		int ans,lans,rans,sum;
		int ans2,lans2,rans2;
		int tag;
	}T[N*4];
	node merge(node A,node B)
	{
		node C;C.ans=C.lans=C.rans=0;
		C.sum=A.sum+B.sum;
		C.ans=max(A.ans,B.ans);C.lans=A.lans;C.rans=B.rans;
		C.ans=max(C.ans,A.rans+B.lans);
		C.lans=max(C.lans,A.sum+B.lans);C.rans=max(C.rans,A.rans+B.sum);
		
		C.ans2=min(A.ans2,B.ans2);C.lans2=A.lans2;C.rans2=B.rans2;
		C.ans2=min(C.ans2,A.rans2+B.lans2);
		C.lans2=min(C.lans2,A.sum+B.lans2);C.rans2=min(C.rans2,B.sum+A.rans2);
		return C;
	}
	void build(int p,int l,int r)
	{
		T[p].ans=T[p].lans=T[p].rans=0;T[p].ans2=T[p].lans2=T[p].rans2=0;
		if(l==r)
		{
			T[p].ans=T[p].lans=T[p].rans=a[l];
			T[p].ans2=T[p].lans2=T[p].rans2=a[l];
			T[p].sum=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	void update(int p,int l,int r,int x,int y,int k)
	{
		if(x<=l&&r<=y)
		{
			T[p].ans=T[p].lans=T[p].rans=k;
			T[p].ans2=T[p].lans2=T[p].rans2=k;
			T[p].sum=k;
			return;
		}
		int mid=(l+r)>>1;
		if(x<=mid)update(p*2,l,mid,x,y,k);
		if(y>mid)update(p*2+1,mid+1,r,x,y,k);
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	node query_max(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
			return T[p];
		int mid=(l+r)>>1;
		if(x<=mid&&y<=mid)return query_max(p*2,l,mid,x,y);
		if(x>mid&&y>mid)return query_max(p*2+1,mid+1,r,x,y);
		return merge(query_max(p*2,l,mid,x,y),query_max(p*2+1,mid+1,r,x,y));
	}
}T;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	T.build(1,1,n);
	scanf("%d",&q);
	while(q--)
	{
		int x,y;
		scanf("%d %d",&x,&y);
		T.update(1,1,n,x,x,y);
		printf("%d\n",max(T.T[1].sum-T.T[1].ans2,max(T.query_max(1,1,n,1,n-1).ans,T.query_max(1,1,n,2,n).ans)));
	}
	return 0;
}

题 \(14\) 【线段树】[USACO08FEB] Hotel G

题目

第一行输入 \(n,m\)，\(n\) 代表有 \(n\) 个房间 \((1\leq n \leq 50,000)\)，编号为 \(1 \sim n\)，开始都为空房，\(m\) 表示以下有 \(m\) 行操作 \((1\leq m < 50,000)\)，以下每行先输入一个数 \(i\) ，表示一种操作：

若 \(i\) 为 \(1\)，表示查询房间，再输入一个数 \(x\)，表示在 \(1,2,...,n\) 房间中找到长度为 \(x\) 的连续空房，输出连续 \(x\) 个房间中左端的房间号，尽量让这个房间号最小，若找不到长度为 \(x\) 的连续空房，输出 \(0\)。若找得到，在这 \(x\) 个空房间中住上人。

若 \(i\) 为 \(2\)，表示退房，再输入两个数 \(x,y\) 代表房间号 \(x \sim x+y-1\) 退房，即让房间为空。

你需要对每个输入 \(1\) 输出对应的答案。

思路

区间查询+区间修改，且信息具有可合并性，还要支持动态查询。所以首选线段树。

先考虑操作 \(1\)，如果整个旅馆都没有连续的 \(x\) 的空房，那么直接输出 \(0\)。否则对线段树进行搜索：

  • 如果左子树有大于等于连续的 \(x\) 个房间，那么返回左子树的答案。
  • 如果左子树的后缀连续 \(0\) 的个数 \(a\) 加上右子树前缀连续 \(0\) 的个数 \(b\) 大于等于 \(x\)，那么返回 \(mid-a+1\)。
  • 最后返回右子树的答案。

这三种情况就包含了所有答案情况了，所以考虑怎么实现，用线段树维护前缀连续 \(0\) 和后缀连续 \(0\) 的个数，还要维护每个区间的最长连续 \(0\) 的个数即可。

修改直接线段树维护即可。

\(Code\):

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 5e4 + 50;
int n,m;
int a[N];
struct Segment
{
	struct node{
		int len,lmax,rmax;
		int sum,tag;
	}T[N * 4];
	void pushup(int p)
	{
		T[p].sum = max(T[p * 2].sum,T[p * 2 + 1].sum);
		T[p].sum = max(T[p].sum,T[p * 2].rmax + T[p * 2 + 1].lmax);
		T[p].lmax = T[p * 2].lmax;T[p].rmax = T[p * 2 + 1].rmax;
		if(T[p * 2].len == T[p * 2].sum)T[p].sum = max(T[p].sum,T[p * 2].len + T[p * 2 + 1].lmax),T[p].lmax = max(T[p].lmax,T[p * 2].len + T[p * 2 + 1].lmax);
		if(T[p * 2 + 1].len == T[p * 2 + 1].sum)T[p].sum = max(T[p].sum,T[p * 2 + 1].len + T[p * 2].rmax),T[p].rmax = max(T[p].rmax,T[p * 2 + 1].len + T[p * 2].rmax);
		return;
	}
	void build(int p,int l,int r)
	{
		T[p].tag = 0;T[p].lmax = T[p].rmax = T[p].sum = T[p].len = r - l + 1;
		if(l == r)
			return;
		int mid = (l + r) >> 1;
		build(p * 2,l,mid);build(p * 2 + 1,mid + 1,r);
		pushup(p);
		return;
	}
	void f(int p,int k)
	{
		if(k == 1)
			T[p].sum = T[p].lmax = T[p].rmax = 0,T[p].tag = 1;
		else
			T[p].sum = T[p].lmax = T[p].rmax = T[p].len,T[p].tag = 2;
		return;
	}
	void pushdown(int p)
	{
		f(p * 2,T[p].tag);f(p * 2 + 1,T[p].tag);
		T[p].tag = 0;
		return;
	}
	void update(int p,int l,int r,int x,int y,int op)
	{
		if(x <= l && r <= y)
		{
			if(op == 1)
				T[p].sum = T[p].lmax = T[p].rmax = 0,T[p].tag = 1;
			else
				T[p].sum = T[p].lmax = T[p].rmax = T[p].len,T[p].tag = 2;
			return;
		}
		if(T[p].tag)pushdown(p);
		int mid = (l + r) >> 1;
		if(x <= mid)update(p * 2,l,mid,x,y,op);
		if(y > mid)update(p * 2 + 1,mid + 1,r,x,y,op);
		pushup(p);
		return;
	}
	int query(int p,int l,int r,int k)
	{
		if(l == r)return l;
		if(T[p].tag)pushdown(p);
		int mid = (l + r) >> 1;
		if(T[p * 2].sum >= k)return query(p * 2,l,mid,k);
		if(T[p * 2].rmax + T[p * 2 + 1].lmax >= k)return mid - T[p * 2].rmax + 1;
		else return query(p * 2 + 1,mid + 1,r,k);
	}
}
T;
int main()
{
	scanf("%d %d",&n,&m);
	T.build(1,1,n);
	for(int i = 1;i <= m;i++)
	{
		int op;
		scanf("%d",&op);
		if(op == 1)
		{
			int x;
			scanf("%d",&x);
			if(T.T[1].sum >= x)
			{
				int ans = T.query(1,1,n,x);
				printf("%d\n",ans);
				T.update(1,1,n,ans,ans + x - 1,op);
			}
			else printf("0\n");
		}
		else
		{
			int x,y;
			scanf("%d %d",&x,&y);
			T.update(1,1,n,x,x + y - 1,op);
		}
	}
	return 0;
}

题 \(15\) 【线段树】买水果

题目

　　　　水果姐今天心情不错，来到了水果街。
　　　　水果街有n家水果店，呈直线结构，编号为1~n，每家店能买水果也能卖水果，并且同一家店卖与买的价格一样。
　　　　学过oi的水果姐迅速发现了一个赚钱的方法：在某家水果店买一个水果，再到另外一家店卖出去，赚差价。
　　　　就在水果姐窃喜的时候，cgh突然出现，他为了为难水果姐，给出m个问题，每个问题要求水果姐从第x家店出发到第y家店，途中只能选一家店买一个水果，然后选一家店（可以是同一家店，但不能往回走）卖出去，求每个问题中最多可以赚多少钱。

思路

预处理出每个区间的最大值与最小值。

先考虑 \(x\le y\) 的情况：

  • 由左子树的答案更新。
  • 由右子树的答案更新。
  • 由右子树的最大值 \(-\) 左子树的最小值更新。

再考虑 \(x>y\) 的情况：

  • 由左子树的答案更新。
  • 由右子树的答案更新。
  • 由左子树的最大值 \(-\) 右子树的最小值更新。

所以线段树适合这些操作，维护区间最大最小值还有记录每个区间的答案。

\(Code\):

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+50;
int n,a[N],q;
struct SegmentTree{
	struct node{
		int ans,maxx,minn,ans2;
	}T[N*4];
	node merge(node a,node b)
	{
		node c;
		c.ans=max(a.ans,b.ans);c.ans2=max(a.ans2,b.ans2);
		c.maxx=max(a.maxx,b.maxx);c.minn=min(a.minn,b.minn);
		c.ans=max(c.ans,b.maxx-a.minn);c.ans2=max(c.ans2,a.maxx-b.minn);
		return c;
	}
	void build(int p,int l,int r)
	{
		T[p].maxx=T[p].minn=T[p].ans=T[p].ans2=0;
		if(l==r)
		{
			T[p].maxx=T[p].minn=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		T[p]=merge(T[p*2],T[p*2+1]);
		return;
	}
	node query(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
			return T[p];
		int mid=(l+r)>>1;
		if(x<=mid&&y<=mid)return query(p*2,l,mid,x,y);
		else if(x>mid&&y>mid)return query(p*2+1,mid+1,r,x,y);
		else return merge(query(p*2,l,mid,x,y),query(p*2+1,mid+1,r,x,y));
	}
}T;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	T.build(1,1,n);
	scanf("%d",&q);
	while(q--)
	{
		int x,y;
		scanf("%d %d",&x,&y);
		if(x<y)printf("%d\n",T.query(1,1,n,x,y).ans);
		else printf("%d\n",T.query(1,1,n,y,x).ans2);
	}
	return 0;
}

题 \(16\) 【线段树】奶牛排队（USACO 2007 January Gold）

题目

　　　　在每天挤奶的时候，农民约翰的N头牛（1≤n≤50000）总是排成一列。有一天，约翰决定与他的牛们一起玩一个极限飞盘游戏。为了简单起见，他将从奶牛队列里面选一定范围内的奶牛来玩这个游戏。然而所有的牛对这个游戏都很感兴趣。农民约翰列出了Q份名单（1≤Q≤200000）和每个奶牛的高度（1≤高度≤1000000）。对于每一份名单，他想你帮助他确定在每份名单中高度最高的奶牛与高度最低的奶牛的高度差是多少。

思路

用线段树求出区间最大最小值，然后再输出区间极差即可，模板题。

\(Code\):

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e4+50;
int a[N],n,q;
struct SegmentTree{
	struct node{
		int maxx,minn;
	}T[N*4];
	void pushup(int p)
	{
		T[p].maxx=max(T[p*2].maxx,T[p*2+1].maxx);
		T[p].minn=min(T[p*2].minn,T[p*2+1].minn);
		return;
	}
	void build(int p,int l,int r)
	{
		if(l==r)
		{
			T[p].maxx=T[p].minn=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		pushup(p);
		return;
	}
	int query_max(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
			return T[p].maxx;
		int mid=(l+r)>>1,res=-2e9;
		if(x<=mid)res=max(res,query_max(p*2,l,mid,x,y));
		if(y>mid)res=max(res,query_max(p*2+1,mid+1,r,x,y));
		return res;
	}
	int query_min(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
			return T[p].minn;
		int mid=(l+r)>>1,res=2e9;
		if(x<=mid)res=min(res,query_min(p*2,l,mid,x,y));
		if(y>mid)res=min(res,query_min(p*2+1,mid+1,r,x,y));
		return res;
	}
}T;
int main()
{
	scanf("%d %d",&n,&q);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	T.build(1,1,n);
	while(q--)
	{
		int l,r;
		scanf("%d %d",&l,&r);
		printf("%d\n",T.query_max(1,1,n,l,r)-T.query_min(1,1,n,l,r));
	}
	return 0;
}

题 \(17\) 【线段树】常见数字Frequent values（POJ3368）

题目

　　　　给你一个含有n个整数的非递减序列a1 , a2 , ... , an，要求你回答一系列的询问，如i和j (1 ≤ i ≤ j ≤ n)，回答出ai , ... , aj之间出现频率最多数字为多少次？

思路

线段树不能维护区间信息并问题，但注意到非递减序列，也就是相同元素是连续的，也就是信息有可合并性，可以考虑线段树，所以我们可以从这下文章。

线段树合并子区间信息时，答案由这几种情况更新：

  • 左子树最大次数与右子树最大次数取一个 \(max\) 更新。
  • 左子树的后缀连续一个数的出现次数加上右子树的前缀连续一个数的出现次数和更新。（前提是左子树的右端点的数要等于右子树的左端点的数）。

\(Code\):

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+50;
int a[N],n,q;
struct SegmentTree{
	struct node{
		int lans,rans,ans;
	}T[N*4];
	void pushup(int p,int l,int r)
	{
		int mid=(l+r)>>1;
		T[p].ans=max(T[p*2].ans,T[p*2+1].ans);T[p].lans=T[p*2].lans;T[p].rans=T[p*2+1].rans;
		if(a[mid]==a[mid+1])
			T[p].ans=max(T[p].ans,T[p*2].rans+T[p*2+1].lans);
		if(a[l]==a[mid]&&a[mid]==a[mid+1])
			T[p].lans=max(T[p].lans,mid-l+1+T[p*2+1].lans);
		if(a[r]==a[mid+1]&&a[mid]==a[mid+1])
			T[p].rans=max(T[p].rans,r-mid+T[p*2].rans);
		return;
	}
	void build(int p,int l,int r)
	{
		T[p].ans=T[p].lans=T[p].rans=0;
		if(l==r)
		{
			T[p].ans=T[p].lans=T[p].rans=1;
			return;
		}
		int mid=(l+r)>>1;
		build(p*2,l,mid);build(p*2+1,mid+1,r);
		pushup(p,l,r);
		return;
	}
	node merge(node A,node B,int l,int r,int x)
	{
		node C;C.lans=C.rans=C.ans=0;
		C.ans=max(A.ans,B.ans);C.lans=A.lans;C.rans=B.rans;
		if(a[x]==a[x+1])
			C.ans=max(C.ans,A.rans+B.lans);
		if(a[x]==a[x+1]&&a[l]==a[x])
			C.lans=max(C.ans,x-l+1+B.lans);
		if(a[x]==a[x+1]&&a[r]==a[x])
			C.rans=max(C.rans,r-x+A.rans);
		return C;
	}
	node query(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)
			return T[p];
		int mid=(l+r)>>1;
		if(x<=mid&&y<=mid)return query(p*2,l,mid,x,y);
		else if(x>mid&&y>mid)return query(p*2+1,mid+1,r,x,y);
		else
		{
			node xx=query(p*2,l,mid,x,y),yy=query(p*2+1,mid+1,r,x,y);
			return merge(xx,yy,max(l,x),min(r,y),mid);
		}
	}
}T;
int main()
{
	scanf("%d %d",&n,&q);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	T.build(1,1,n);
	while(q--)
	{
		int l,r;
		scanf("%d %d",&l,&r);
		printf("%d\n",T.query(1,1,n,l,r).ans);
	}
	return 0;
}
posted @ 2023-12-31 17:51  CQWYB  阅读(15)  评论(0)  编辑  收藏  举报