[题解]Codeforces Round #519 - B. Lost Array
【题目】
【描述】
Bajtek有一个数组x[0],x[1],...,x[k-1]但被搞丢了，但他知道另一个n+1长的数组a，有a[0]=0，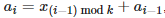
对i=1,2,...,n。由此可以找到数组x[0],x[1],...,x[k-1]的一些可能情况，即满足这个关系的数组x[0],x[1],...,x[k-1]。问一共有多少种可能的数组x[0],x[1],...,x[k-1]的长度k，输出可能的数量以及所有可能的长度k。
数据范围：1<=n<=1000，1<=a[i]<=10^6（这里不包括a[0]，默认a[0]=0）
【思路】
先不考虑数组x是循环的，即不考虑数组x是有限长的，那么由数组a可以反解出与数组a等长的一个数组“x”，我们要找的真正的数组x实际上是这个反解出来的“x”的一个周期，我们要找的就是这个“x”有多少种周期长度。
要验证i是不是“x”的一个周期长度，则将“x”的元素分为i组，即下标模i相同的分到一组，检查每一组从前往后数第某个元素是不是都是相同的。这里复杂度是O(n)的。
对i进行枚举，即可找到所有可能的周期长度。至此复杂度为O(n^2)。
【我的实现】
复杂度：O(n^2)
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 6 using namespace std; 7 #define MaxN 1020 8 int x[MaxN]; 9 int Ans[MaxN]; 10 11 int main() 12 { 13 int n; 14 int a, pre_a = 0; 15 int i, j, k; 16 //int cur; 17 bool flag; 18 scanf("%d", &n); 19 for(i = 1; i <= n; i++) 20 { 21 scanf("%d", &a); 22 x[i-1] = a - pre_a; 23 pre_a = a; 24 } 25 for(i = 1; i <= n; i++) //step = i 26 { 27 flag = false; 28 for(j = 0; j < i; j++) //start at j for each zhouqi 29 { 30 for(k = j; k < n; k += i) 31 { 32 if(k > j && x[k] != x[k-i]) 33 { 34 flag = true; 35 break; 36 } 37 } 38 if(flag) 39 break; 40 } 41 if(!flag) 42 Ans[++Ans[0]] = i; 43 } 44 printf("%d\n", Ans[0]); 45 for(i = 1; i <= Ans[0]; i++) 46 printf("%d ", Ans[i]); 47 return 0; 48 }
【评测结果】
