飞扬的小鸟

题目描述

Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度，让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话，便宣告失败。

为了简化问题，我们对游戏规则进行了简化和改编：

1. 游戏界面是一个长为n ，高为 m 的二维平面，其中有k 个管道（忽略管道的宽度）。

2. 小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。

3. 小鸟每个单位时间沿横坐标方向右移的距离为1 ，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度X ，每个单位时间可以点击多次，效果叠加；

如果不点击屏幕，小鸟就会下降一定高度Y 。小鸟位于横坐标方向不同位置时，上升的高度X 和下降的高度Y 可能互不相同。

4. 小鸟高度等于0 或者小鸟碰到管道时，游戏失败。小鸟高度为 m 时，无法再上升。

现在，请你判断是否可以完成游戏。如果可以 ，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

输入输出格式

输入格式：

 

输入文件名为 bird.in 。

第1 行有3 个整数n ，m ，k ，分别表示游戏界面的长度，高度和水管的数量，每两个

整数之间用一个空格隔开；

接下来的n 行，每行2 个用一个空格隔开的整数X 和Y ，依次表示在横坐标位置0 ~n- 1

上玩家点击屏幕后，小鸟在下一位置上升的高度X ，以及在这个位置上玩家不点击屏幕时，

小鸟在下一位置下降的高度Y 。

接下来k 行，每行3 个整数P ，L ，H ，每两个整数之间用一个空格隔开。每行表示一

个管道，其中P 表示管道的横坐标，L 表示此管道缝隙的下边沿高度为L ，H 表示管道缝隙

上边沿的高度（输入数据保证P 各不相同，但不保证按照大小顺序给出）。

 

输出格式：

 

输出文件名为bird.out 。

共两行。

第一行，包含一个整数，如果可以成功完成游戏，则输出1 ，否则输出0 。

第二行，包含一个整数，如果第一行为1 ，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

 

输入输出样例

输入样例#1：

10 10 6 
3 9  
9 9  
1 2  
1 3  
1 2  
1 1  
2 1  
2 1  
1 6  
2 2  
1 2 7 
5 1 5 
6 3 5 
7 5 8 
8 7 9 
9 1 3 

输出样例#1：

1
6

输入样例#2：

10 10 4 
1 2  
3 1  
2 2  
1 8  
1 8  
3 2  
2 1  
2 1  
2 2  
1   2  
1 0 2 
6 7 9 
9 1 4 
3 8 10  

输出样例#2：

0
3

说明

【输入输出样例说明】

如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

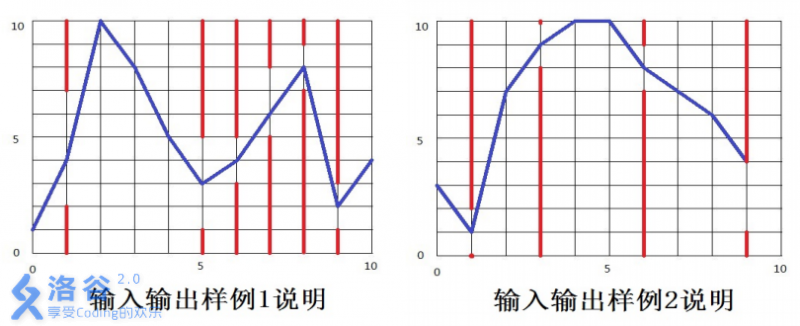
【数据范围】

对于30% 的数据：5 ≤ n ≤ 10，5 ≤ m ≤ 10，k = 0 ，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于50% 的数据：5 ≤ n ≤ 2 0 ，5 ≤ m ≤ 10，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于70% 的数据：5 ≤ n ≤ 1000，5 ≤ m ≤ 1 0 0 ；

对于100%的数据：5 ≤ n ≤ 100 0 0 ，5 ≤ m ≤ 1 0 00，0 ≤ k < n ，0<X < m ，0<Y <m，0<P <n，0 ≤ L < H ≤ m ，L +1< H 。

思路：

　　首先是个dp。

　　数组f[i][j]表示，到达i,j这个位置,最少的点击次数。

　　转移方程

　　　　　　f[i][j]=min

　　　　　　　　　　{  

　　　　　　　　　　　f[ i-1 ][ j-up[i-1] ]+1  ,(从前一个跳过来）j>=up[i-1]

　　　　　　　　　　　f[ i ][ j-up[i-1] ]+1,(连续点击得到),j>=up[i-1].

　　　　　　　　　　　f[ i-1 ][ j+down[i-1] ] (下落得到 ）j+down[i-1] <=m

　　　　　　　　　　}

　　　　　　特别的f[i][m]=

　　　　　　　　　　   min{ f[ i ][ j ]+1,f[ i-1 ][ j]+1}, j+up[i-1]>=m　

 

#include<iostream>
#include<queue>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int n,m,k;
const int N=10010;
int f[N][N/10];
int up[N],down[N];
int top[N],end[N],have[N]; 
int maxx=0;
const int INF=99999999;
int main()
{
//freopen("bird.in","r",stdin);
//    freopen("bird.out","w",stdout); 
    scanf("%d%d%d",&n,&m,&k);
    for(int i=0;i<n;i++)
        scanf("%d%d",&up[i],&down[i]);    
    for(int i=0;i<=n;i++)
        top[i]=m+1,end[i]=0,have[i]=0;
    
    for(int i=1;i<=k;i++)
    {
        int x;scanf("%d",&x);
        scanf("%d%d",&end[x],&top[x]);have[x]=1;
    }
    memset(f,0,sizeof(f));
    for(int i=1;i<=n;i++)
    for(int j=0;j<=m;j++)
        f[i][j]=INF;
    f[0][0]=INF;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(j>=up[i-1])
            {
                f[i][j]=min(f[i][j],f[i-1][j-up[i-1]]+1);    
                 f[i][j]=min(f[i][j],f[i][j-up[i-1]]+1);
            }
            if(j==m)            
            for(int p=m-up[i-1];p<=m;p++)
            {
                f[i][m]=min(f[i][m],f[i-1][p]+1);
                f[i][m]=min(f[i][m],f[i][p]+1);
            }
            
        }
        for(int j=end[i]+1;j<=top[i]-1;j++)
        {  
            if(j+down[i-1]<=m)
                f[i][j]=min(f[i][j],f[i-1][j+down[i-1]]);
        }
        for(int j=1;j<=end[i];j++) f[i][j]=INF;
        for(int j=top[i];j<=m;j++) f[i][j]=INF;
    }
    int ans=INF,tot=k;
    for(int i=n;i>=1;i--)
    {
        for(int j=end[i]+1;j<=top[i]-1;j++)
             ans=min(ans,f[i][j]);
        if(ans!=INF) break;
        if(have[i]) tot--;
    }
    if(tot==k)
        printf("1\n%d",ans);    
    else
        printf("0\n%d",tot);
    return 0;
    
}