套题8.20
T1
【问题描述】
在银行柜台前，有 n 个顾客排队办理业务。队伍中从前往后，第 i 位顾客办理业务需要
t i 分钟时间。一位顾客的等待时间定义为：队伍中在他之前的所有顾客和他自己的办理业务
时间的总和。 第 i 位顾客有一个最长等待时间 d i ， 如果超过了时间 d i ， 业务还没有办理完成，
那么这位顾客就会觉得不满意。具体来说，假设第 i 位顾客的等待时间为 f i ，若 f i > d i ，则这
位顾客的不满意度为 f i -d i ，否则不满意度为 0。
你作为银行里的职员， 需要安排这 n 位顾客的初始排队顺序， 使得不满意度最大的那位
顾客不满意度最小。
【输入】
输入的第 1 行包含一个正整数 n，表示顾客的数量。
输入的第 2 行包含 n 个正整数，第 i 个数表示 t i ，单位为分钟。
输入的第 3 行包含 n 个正整数，第 i 个数表示 d i ，单位为分钟。
【输出】
输出包含 1 个整数，表示最大不满意度的最小值。
【输入输出样例 1】
transact.in transact.out
3
5 8 10
11 15 13
8
见选手目录下的 transact / transact1.in 与 transact / transact1.out
【输入输出样例 1 说明】
排队顺序 1 3 2
业务办理时间 5 10 8
等待时间 5 15 23
最长等待时间 11 13 15
不满意度 0 2 8
最大不满意度为 8。这是最大不满意度能达到的最小值。
【输入输出样例 2】
见选手目录下的 transact / transact2.in 与 transact / transact2.out
【数据规模与约定】
对于 50%的数据，n≤10
对于 70%的数据，n≤1,000
对于 100%的数据，n≤100,000，1≤t i ≤10 4 ，0≤d i ≤10 9
有点贪心吧，有耐性的放在后边显然比没耐心的放在后边的不满意度小。
那么，就按照耐心排一下序，取一遍max
#include<iostream> #include<cstdio> #include<queue> #include<vector> #include<algorithm> #include<cstring> using namespace std; struct node{ int t,d; }a[100009]; int n; bool cmp(node x,node y){return x.d<y.d;} int main() { freopen("transact.in","r",stdout); freopen("transact.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i].t); for(int i=1;i<=n;i++) scanf("%d",&a[i].d); sort(a+1,a+1+n,cmp); long long tot=0,maxn=0; for(int i=1;i<=n;i++) { tot+=a[i].t; if(tot>a[i].d) maxn=max(maxn,tot-a[i].d); } cout<<maxn; return 0; }
2.传球接力
（pass.cpp/c/pas）
【问题描述】
n 个小朋友在玩传球。小朋友们用 1 到 n 的正整数编号。每个小朋友有一个固定的传球
对象，第 i 个小朋友在接到球后会将球传给第 a i 个小朋友，并且第 i 个小朋友与第 a i 个小朋
友之间的距离为 d i 。
一次传球接力是这样进行的：由一个小朋友发球，将球传给他的传球对象，之后接到球
的小朋友再将球传给自己的传球对象，如此传球若干次后停止。期间，包括发球者在内，每
个小朋友至多只能拿到球一次。一次传球接力的总距离是每次传球的距离的总和。
小朋友们想进行一次总距离最长的传球接力， 现在需要你帮助他们求出满足上述要求的
传球接力的最长总距离。
【输入】
输入的第 1 行包含 1 个整数 n。
接下来的 n 行，第 i 行包含两个整数 ai 和 di，意义如题目中所述，两个数间用一个空格
隔开。
【输出】
输出包含 1 个数，表示传球接力总距离的最大值。
【输入输出样例 1】
pass.in pass.out
5
2 1
3 2
4 1
2 3
3 3
7
见选手目录下的 pass / pass1.in 与 pass / pass1.out
【输入输出样例 1 说明】
由第 5 个小朋友发球，传给第 3 个小朋友，再传给第 4 个小朋友，总距离为 3+1+3=7
【输入输出样例 2】
见选手目录下的 pass / pass2.in 与 pass / pass2.out
【数据规模与约定】
对于 50%的数据，n≤1,000
对于 100%的数据，n≤500,000，1≤a i ≤n，a i ≠i，1≤d i ≤10,000
开始只写了80分栈溢出（递归层数太多了）
#include<iostream>
#include<cstdio>
#include<queue>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
int n,a[500009],d[500009];
int f[500009],maxn,first,last;
bool vis[500009],o[500009];
void work()
{
int tot=f[first];
for(int i=first;i;i=a[i])
{
o[i]=1;
f[a[i]]=tot-d[i];
if(a[i]==first) break;
}
}
int dfs(int x)
{
vis[x]=1;
if(!vis[a[x]]) f[x]=d[x]+dfs(a[x]);
else
f[x]=d[x]+f[a[x]],first=a[x],last=x;
if(x==first&&(!o[x])) work(),first=last=0;
return f[x];
}
int main()
{
freopen("pass.in","r",stdout);
freopen("pass.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&a[i],&d[i]);
for(int i=1;i<=n;i++)
if(!vis[i])
dfs(i);
for(int i=1;i<=n;i++)
maxn=max(maxn,f[i]);
printf("%d",maxn);
return 0;
}
然后，参考了题解，终于A了。
既要处理环，还要统计环外的长度。单独处理的话，麻烦+费时。
不知哪位大神想到了这种做法：
（1）找入度为零的点U，加入队列Q，它所连的点V入度减1，如果点V的入度也变为了1，V也加入队列。
（2）在进行（1）的同时，处理出从叶节点到环上的根的最大长度。
（3）现在已经缩成一个环了，剩下的就是处理环上某个点走一圈的长度（不能走回起点，而是和起点相邻的点）。
（4）在处理出（3）之后，加上叶到该点的最大长度，维护最大值。
#include<iostream>
#include<cstdio>
#include<queue>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
int n,a[500009],d[500009];
int f[500009];
long long maxn=0;
bool vis[500009];
int ru[500009],pre[500009];
queue<int>q;
int main()
{
freopen("pass.in","r",stdin);
freopen("pass.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&a[i],&d[i]),ru[a[i]]++;
for(int i=1;i<=n;i++)
if(ru[i]==0) q.push(i);
int u,v;
while(!q.empty())
{
u=q.front(),q.pop();
v=a[u];
f[v]=max(f[v],d[u]+f[u]);
--ru[v];
if(!ru[v]) q.push(v);
}//缩成环
for(int i=1;i<=n;i++)
if(ru[i]&& ( !vis[i] ))
{
u=i;long long tot=0;
do
{
vis[u]=1;
q.push(u);
pre[a[u]]=d[u];
tot+=d[u];
u=a[u];
}while(u!=i);
while(!q.empty())
{
u=q.front(),q.pop();
long long sum=(long long )(tot-pre[u]+f[u]);
if(sum>maxn) maxn=sum;
}
}
printf("%lld\n",maxn);
return 0;
}
3.捡金币（coin.cpp/c/pas）
【问题描述】
小空正在玩一个叫做捡金币的游戏。 游戏在一个被划分成n行n列的网格状场地中进行。
每一个格子中都放着若干金币， 并且金币的数量会随着时间而不断变化。 小空的任务就是在
网格中移动，拾取尽量多的金币。并且，小空还有一个特殊技能“闪现”，能帮助她在网格间
快速移动。
捡金币游戏的具体规则如下：在每一秒开始时，每个网格内都会出现一定数量的金币，
而之前在这格没有被拾取的金币就消失了。在游戏开始时，也就是第 1 秒的开始，小空可以
选择任意一个网格作为起点开始本次游戏，并拾取起点内的金币。之后，在下一秒到来前，
小空可以选择走路移动到与她所在的格子上、下、左、右相邻的一个格子中，或者呆在原地
不动， 并在下一秒开始时拾取到她所在的格子中的金币。 或者， 小空可以选择使用闪现技能，
使用一次闪现时，她先选择上、下、左、右一个方向，之后向该方向移动两格。小空可以在
一秒内使用多次闪现，但不能超过 C 次。在一秒内使用的多次闪现必须向同一个方向移动，
若使用 x 次闪现，便可以向一个方向移动正好 2x 格，并且她也只能在下一秒开始时收集到
连续闪现结束后所在的那一格中的金币。 如果在某一秒钟小空使用了闪现， 那么她就不能选
择通过走路移动了，反过来也是如此。无论走路或者使用闪现，小空都不能移动到整个场地
之外。整个游戏共进行 T 秒，在第 T 秒开始时，小空将会拾取她所在的格子中的金币，并结
束游戏。小空在整局游戏内一共只能使用最多 W 次闪现。
举个例子，在如下 3*3 的场地中，游戏共进行 3 秒，下表列出了 3 秒开始时每一格内的
金币数量。
如果小空选择在第 1 行第 1 列开始游戏， 那么在第 1 秒开始时她会获得 1 枚金币。 接下
来，如果她选择向右走，那么在第 2 秒开始时她会出现在第 1 行第 2 列并获得 3 枚金币。接
下来，过她选择向下进行 1 次闪现，那么在第 3 秒开始时她会出现在第 3 行第 2 列并获得 2
枚金币，游戏结束，一共获得 6 枚金币。
又如，在如下 5*5 的场地中（只列出了第 1 行所含金币数） ，游戏共进行 2 秒，如果小
空选择在第 1 行第 1 列开始游戏，则她会获得 1 枚硬币，之后若向右连续闪现 2 次，那么在
第 2 秒开始时她会出现在第 1 行第 5 列，并获得 2 枚硬币，总共获得 3 枚硬币。
现在，给出游戏场地的大小 n，每秒钟开始时各个位置会出现的金币数，小空一秒内最
多使用闪现的次数 C，小空在整局游戏中使用闪现的最多次数 W，整局游戏的总时间 T，请
你告诉小空她最多可以获得多少枚金币。
【输入】
输入的第 1 行包含 4 个整数 n，C，W，T，意义如问题描述中所述。
接下来包含 n 个 n*n 的矩阵，第 k 个矩阵的第 i 行第 j 列表示第 i 行第 j 列的格子在第 k
秒开始时出现的金币数（记作s i,j,k ） 。相邻两个矩阵间用一个空行隔开。
【输出】
输出包含一个整数，表示游戏结束时小空最多可以获得的金币数量。
【输入输出样例 1】
coin.in coin.out
3 1 1 3
1 3 4
3 2 1
1 3 2
2 3 1
1 3 2
2 1 4
3 3 1
3 2 1
2 3 1
11
见选手目录下的 coin / coin1.in 与 coin / coin1.out
【输入输出样例 1 说明】
选择在第 1 行第 3 列开始游戏，获得 4 枚金币；在第 2 秒开始时向下闪现到第 3 行第 3
列，获得 4 枚金币；在第 3 秒开始时向左走到第 3 行第 2 列，获得 3 枚金币，游戏结束。一
共获得 11 枚金币。
【输入输出样例 2】
见选手目录下的 coin / coin2.in 与 coin / coin2.out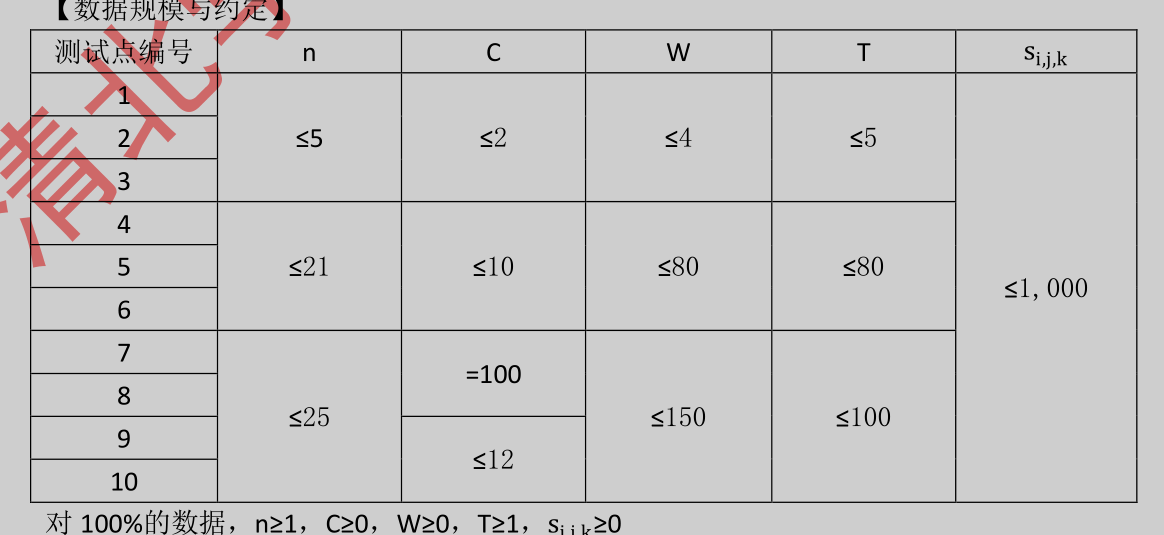
可以看出应该是个dp，状态是 f[t][i][j][k]表示时间t时（i,j）位置，闪现K次 的金币数。
如果只是走路的话那就是一个简单的dp。但，事与愿违啊。。
【闪现】的出现打乱了我们的部署，因为每一秒能闪现C次，如果再去枚举闪现次数的话。复杂度就达到了O( T * n^2 * W *C ) 达到了10^8以上。当然，C比较小的时侯如C<=30 时，勉强能过80分（前提是你把时间开到了3s）
但为了能优雅的过这道题，我们维护一个单调队列q[i]，表示该行前i列的最大值。 这样，完美的A掉了它。
#include<iostream> #include<queue> #include<cstring> #include<vector> #include<cstdio> #include<algorithm> using namespace std; #define INF 1000000007 int a[209][30][30],f[2][30][30][209]; int q[30],qc[30],v[30][209]; int cnt,n,C,W,T,i,j,k,ii,jj,kk,t,tt,l,r; int ans,ch,tag; void up(int &x,int y) { if(y>x) x=y; } void clear() { l=1,r=0; q[0]=INF; q[1]=-INF; cnt=0; } void push(int x) { q[++r]=x; q[r+1]=-INF; qc[r]=1; while(q[r] >= q[r-1]) { qc[r-1]+=qc[r]; q[r-1]=q[r]; q[r--]=-INF; } if(++cnt>C) if(--qc[l] == 0) q[l++]=INF; } int main() { freopen("coin.in","r",stdin); freopen("coin.out","w",stdout); scanf("%d%d%d%d",&n,&C,&W,&T); for(t=1;t<=T;t++) for(i=1;i<=n;i++) for(j=1;j<=n;j++) scanf("%d",&a[t][i][j]); for(i=1;i<=n;i++) for(j=1;j<=n;j++) f[0][i][j][0] = a[1][i][j]; t=0; for(tt=2;tt<=T;tt++) { t= t^1; for(i=1;i<=n;i++) for(j=1;j<=n;j++) for(k=0;k<=W;k++) f[t][i][j][k]= -INF; for(i=1;i<=n;i++) { ++tag; for(jj=1;jj<=n;jj++) for(kk=0;kk<=W;kk++) if(v[jj][kk]!=tag) { clear(); j=jj; k=kk; while(j<=n&&k<=W) { v[j][k]=tag; up(f[t][i][j][k],q[l]); push(f[t^1][i][j][k]); j+=2;//右闪 k++; } } ++tag; for(jj=n;jj>=1;jj--) for(kk=0;kk<=W;kk++) if(v[jj][kk]!=tag) { clear(); j=jj; k=kk; while(j>=1&&k<=W) { v[j][k]=tag; up(f[t][i][j][k],q[l]); push(f[t^1][i][j][k]); j-=2;//左闪 k++; } } } for(j=1;j<=n;j++) { ++tag; for(ii=1;ii<=n;ii++) for(kk=0;kk<=W;kk++) if(v[ii][kk]!=tag) { clear(); i=ii; k=kk; while(i<=n&&k<=W) { v[i][k]=tag; up(f[t][i][j][k],q[l]); push(f[t^1][i][j][k]); i+=2;//右闪 k++; } } ++tag; for(ii=n;ii>=1;ii--) for(kk=0;kk<=W;kk++) if(v[ii][kk]!=tag) { clear(); i=ii; k=kk; while(i>=1&&k<=W) { v[i][k]=tag; up(f[t][i][j][k],q[l]); push(f[t^1][i][j][k]); i-=2;//左闪 k++; } } } for(i=1;i<=n;i++) for(j=1;j<=n;j++) for(k=0;k<=W;k++) { up(f[t][i][j][k],f[t^1][i-1][j][k]); up(f[t][i][j][k],f[t^1][i+1][j][k]); up(f[t][i][j][k],f[t^1][i][j-1][k]); up(f[t][i][j][k],f[t^1][i][j+1][k]); up(f[t][i][j][k],f[t^1][i][j][k]); f[t][i][j][k]+=a[tt][i][j]; } } for(i=1;i<=n;i++) for(j=1;j<=n;j++) for(k=0;k<=W;k++) up(ans,f[t][i][j][k]); cout<<ans; return 0; }
