Conditional Probability Models for Deep Image Compression

目录

• 简介
• 模型
  • Quantization
  • Entropy estimation

简介

\(\quad\)训练这种基于网络的压缩方法有一个关键的挑战：优化编码器中潜在表示的比特率R，为了使用数量有限的比特对图像进行编码，需要将潜在的表示离散化映射到有限值的集合。而离散化是不可微的，这就给基于梯度的优化方法带来挑战，人们提出很多方法来解决这个问题。
\(\quad\)本文重点就是如何对熵进行建模以便在优化过程中权衡\(D+\lambda H(R)\)
\(\quad\)该文章提出的模型基于上下文模型，上下文模型之前被用来证明已训练模型的编码率，直接作为优化项中的熵。同时训练自动编码器和上下文模型，其中上下文模型学习图像表征的卷积概率模型，而自动编码器则利用它进行熵估计，以实现速率-失真权衡。

模型

Quantization

\(\quad\)量化过程是把连续的数 离散到有限数集中，减少储存压力，但是要处理好反向传播的问题。

\[\hat{z}_i=Q(z_i):=\arg\min_j\|z_i-c_j\|, \]

思考：这个有限的数集如何确定？
在反向传播时，使用如下软量化

\[\tilde{z}_i=\sum_{j=1}^L\frac{\exp(-\sigma\|z_i-c_j\|)}{\sum_{l=1}^L\exp(-\sigma\|z_i-c_l\|)}c_j \]

Entropy estimation

\(\quad\)这篇文章在PixelRNN的基础上，将离散后的概率分布分解为条件概率的累乘。

\[p(\hat{\mathbf{z}})=\prod_{i=1}^mp(\hat{z}_i|\hat{z}_{i-1},\ldots,\hat{z}_1), \]

然后使用神经网络\(P(\hat z)\)作为上下文模型，来估计条件概率。过程为：
使用

\[P_{i,l}(\hat{\mathbf{z}})\approx p(\hat{z}_i=c_l|\hat{z}_{i-1},\ldots,\hat{z}_1), \]

作为向量\(\hat z\)中第i个位置量化为有限集C中元素l的概率。将这种近似的概率分布称为\(q(\hat z)\)
由于这种条件分布\(p(\hat{z}_i|\hat{z}_{i-1},\ldots,\hat{z}_1)\)只依赖之前的值\(\hat{z}_{i-1},\ldots,\hat{z}_1\),这就对网络P施加了因果约束。因为如果想在网络P中并行的计算\(P_{i,l}\)，就必须保证它只依赖之前的\(\hat{z}_{i-1},\ldots,\hat{z}_1\)。
\(\quad\)为了学习P，训练P的最大似然，或者使用交叉熵损失来训练\(P_i\)来对\(\hat z_i\)在C中的序号进行分类。（交叉熵损失如下）

\[CE:=\mathbb{E}_{\hat{z}\sim p(\hat{z})}[\sum_{i=1}^{m}-\log P_{i,I(\hat{z}_{i})}]. \]

我们学习\(P\)使得\(P=q\approx p\)可以使用交叉熵作为熵的估计。所以，在训练自编码器的时候，可以通过最小化CE间接最小化H。因此编码成本为：

\[C(\hat{\mathbf{z}}):=\sum_{i=1}^{m}-\log P_{i,I(\hat{z}_{i})}, \]

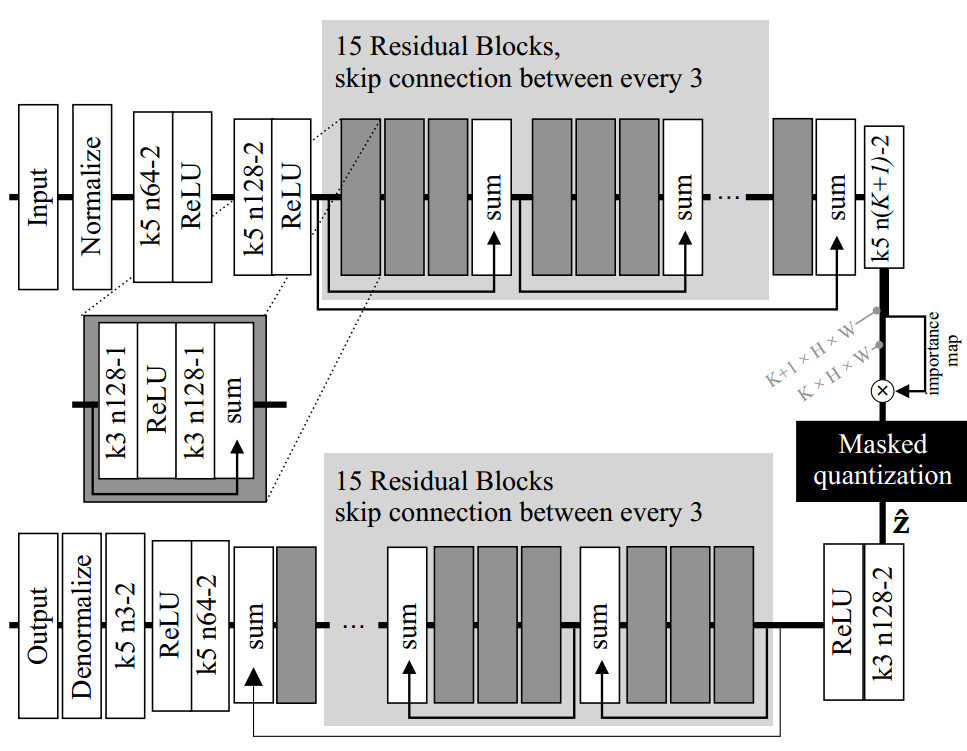
整个模型结构如图所示：

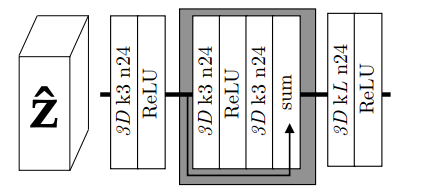
上下文概率模型结构如图所示：

对量化后的结果进行概率统计。