Checkerboard Context Model for Efficient Learned Image Compression

目录

• Abstract
• Introduction
• Preliminary 初步介绍
  • Variational Image Compression with Hyperprior(超先验变分图像压缩)
  • Autoregressive Context(自回归上下文模型)
• Parallel Context Modeling 并行上下文模型
  • Random-Mask Model: Test Arbitrary Masks(随机掩码模型)
  • How Distance Influences Rate Saving
  • Parallel Decoding with Checkerboard Context（棋盘模型并行解码）

Abstract

自回归模型有效提高了RD表现，因为它有效减少了潜表示的空间冗余，但其解码时需要按照特定的顺序，而不能并行。本文的棋盘上下文模型，重新组织解码顺序，解码速度快了40倍。

Introduction

减少冗余的三个途径，空间、视觉和统计冗余。JPEG,JPEG2000 and BPG 都是用无损熵编码，内容损失只发生在量化阶段。

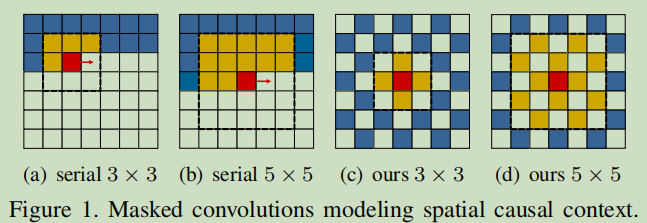
图1为空间因果上下文的掩码卷积模型，红色块代表要编码/解码的部分，Latents in yellowand blue locations are currently visible (all of them are visible during encoding, and those who have been decoded are visible during decoding).上下文模型可使用掩码卷积来进行上下文建模，以红色块为中心，与黄色块做卷积。
图(a)(b)是常用的串行上下文模型。(c)(d)是棋盘模型，当黄色与蓝色位置解码后，其他位置都可以并行解码。

Preliminary 初步介绍

Variational Image Compression with Hyperprior(超先验变分图像压缩)

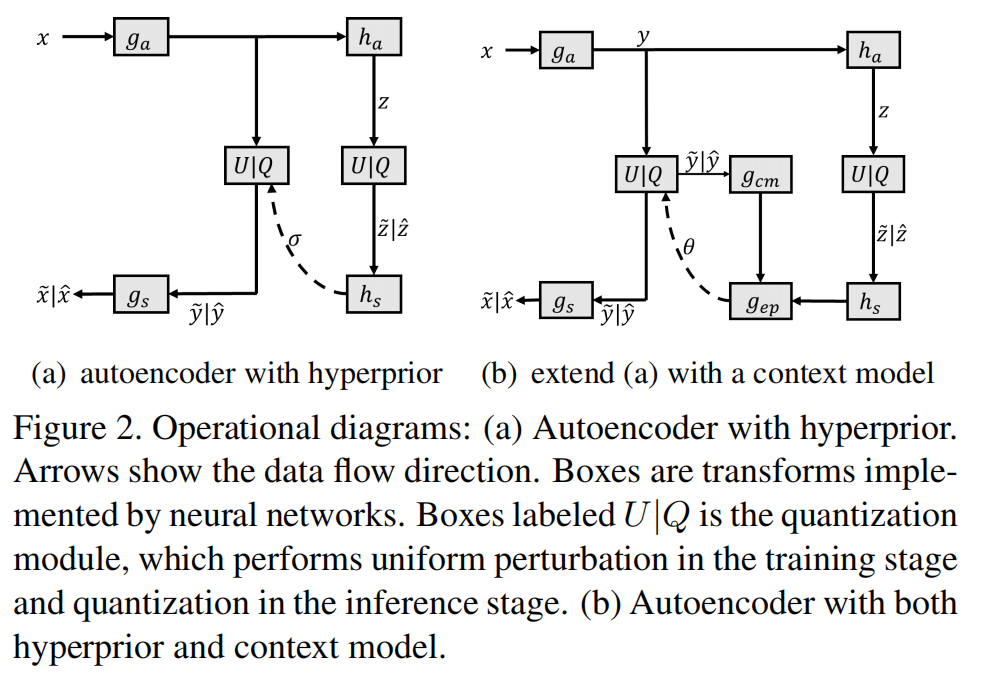
尺度超先验框架如图2所示，
\(\quad\) \(g_s\),\(h_a\),\(h_s\)是神经网络实现的nonlinear transforms
\(\quad\) \(x\)是原始图像
\(\quad\) \(y=g_a(x)\)和\(\hat{y}=Q(y)\),分别是量化前后的 latent representations
\(\quad\) \(\hat{x}=g_s(\hat{y})\)是重构图像。
\(\quad\) \(z=h_a(y)\)和\(\hat{z}=Q(z)\),分别是量化前后的hyper latent
\(\quad\) \(\hat{z}\)被用作边信息，为latent \(\hat{y}\)的熵模型估计尺度参数\(\sigma\)
在训练时，通过加均匀噪声来近似量化操作，得到可微的\(\tilde{y},\tilde{z},\tilde{x}\)
The tradeoff between rate and distortion(loss function):

\[\begin{aligned} \begin{aligned}R+\lambda\cdot D\end{aligned}& \begin{aligned}&=\mathbb{E}_{\boldsymbol{x}\sim p_{\boldsymbol{x}}}[-\log_{2}p_{\boldsymbol{\hat{y}}|\boldsymbol{\hat{z}}}(\boldsymbol{\hat{y}}|\boldsymbol{\hat{z}})-\log_{2}p_{\boldsymbol{\hat{z}}}(\boldsymbol{\hat{z}})]\end{aligned} \\ &+\lambda\cdot\mathbb{E}_{\boldsymbol{x}\sim p_{\boldsymbol{x}}}|d(\boldsymbol{x},\boldsymbol{x})| \end{aligned}\]

其中，\(\hat{y}\) 和 hyper latent \(\hat{z}\)通过估计熵来预测， \(\lambda\) controls the bit rate,\(\lambda\)越大，图像重构质量越好。D通常用评价指标MSE或者MS-SSIM.E是指数分布
使用超先验尺度scale hyperprior，latents, \(\hat{y}\)的概率可以通过条件高斯尺度混合模型(GSM)来进行建模:

\[\begin{aligned}p_{\boldsymbol{\hat{y}}|\boldsymbol{\hat{z}}}(\hat{y}_i|\boldsymbol{\hat{z}})&=\left[\mathcal{N}(\mu_i,\sigma_i^2)*\mathcal{U}(-\frac12,\frac12)\right](\hat{y}_i)\end{aligned} \]

\[p_{\boldsymbol{\hat{y}}|\boldsymbol{\hat{z}}}(\boldsymbol{\hat{y}}|\boldsymbol{\hat{z}})=\prod_ip_{\boldsymbol{\hat{y}}|\boldsymbol{\hat{z}}}(\hat{y}_i|\boldsymbol{\hat{z}}) \]

其中，位置参数\(\mu_i\)假设为0，尺度参数\(\sigma_i\)是\(\sigma=h_s(\hat{z})\)第i个元素，因为\(\hat{y}\)中每个代码给定了超先验。hyper latent \(\hat{z}\)的概率可以用为参数全因分解密度模型建模。

Autoregressive Context(自回归上下文模型)

\(\quad\)自回归上下文模型包括自编码器(\(g_a,g_s\)),超自动编码器（\(h_a,h_s\)）,上下文模型\(g_cm\),用于估计潜在 y 的熵模型位置参数和比例参数Φ = (µ,σ)的参数推理网络\(g_{ep}\)
\(\quad\) \(h_s(\hat{z})\)表示超先验特征，\(g_{cm}(\hat{y}_{<i})\)表示上下文特征
the parameter prediction for i-th representation \(yˆi\) is:

\[\begin{aligned} \phi_i=(\mu_i,\sigma_i)=g_{ep}(h_s(\hat{z}),g_{cm}(\hat{y}_{<i})) \end{aligned} \]

\(\quad\)其中，\(\hat{y}_{<i}\) 表示因果上下文（即潜变量 \(\hat{y}_i\) 附近的一些可见潜变量）。这种上下文模型可以通过掩码卷积实现。给一个\(k\times k\)的二进制掩码M，和卷积权重W，有\(k\times k\)卷积核的掩码卷积，可以将x以重新参数化的形式表示。

\[\begin{aligned} g_{cm}(x)=(M \bigodot W)x+b \end{aligned} \]

其中， \bigodot是Hadamard (哈达玛乘积，即矩阵对应元素相乘)。M描述了上下文模型建模，通过手动设置不同掩码M

通过手动设置不同的掩码 M 可以获得各种上下文参照方案 就能获得不同的上下文参照方案。

Parallel Context Modeling 并行上下文模型

Random-Mask Model: Test Arbitrary Masks(随机掩码模型)

\(\quad\)上下文模型可视为权重W以二进制掩码M为条件的卷积，在以下公式中掩码M描述了上下文的模型的模式。

\[\begin{aligned} g_{cm}(x)=(M \bigodot W)x+b \end{aligned} \]

每次反向传播，权重W会在随机掩码的引导下更新，这就隐含地建立了一个由所有以 5×5 掩码为条件的上下文模型组成的超级网。
这种随机掩码模型适合度量各种上下文模型带来的保存比特率的能力。保存失真率的能力被定义为：
\(R_0\)表示每位比特的非参考位，\(R_M\)表示将掩码 M 输入随机掩码模型的 BPP。

How Distance Influences Rate Saving

串行模型保留失真率是通过参考已经解码相邻潜变量(latents)来更精准的预测当前解码潜变量的熵。通过使用上述随机掩码模型，我们发现位置越近，减少的比特率越多。

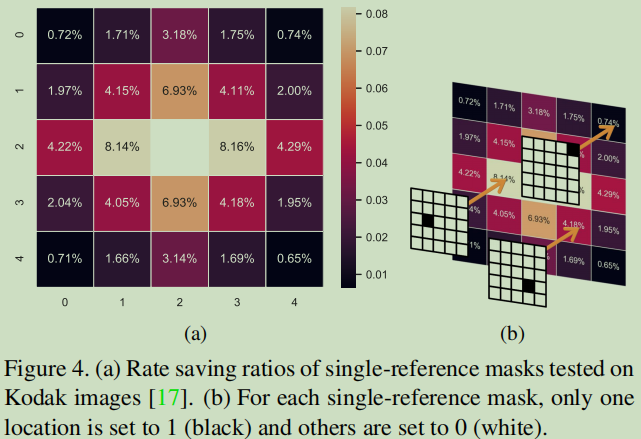
通过上下文建模，熵模型基于已经解码的潜变量\(\hat{y}_{i<j}\)预测解码潜变量\(\hat{y_j}\)
以上研究证明了使用并行的

Parallel Decoding with Checkerboard Context（棋盘模型并行解码）

现进行一次编码，在解码时，先解码锚点的元素，然后解码其他元素。