ML——week3

七、正则化(Regularization)

7.1 过拟合的问题

线性回归和逻辑回归能够有效地解决许多问题，但是当将它们应用到某些特定的机器学习场景时，会遇到过拟合(over-fitting)的问题，可能会导致它们效果很差。因此，我们需要一种正则化(regularization)的技术，它可以改善或者减少过度拟合问题。

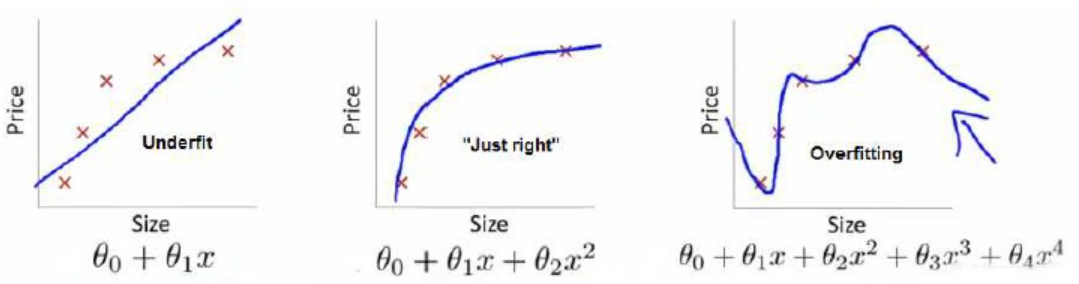
左图是一个线性模型，欠拟合，不能很好的适应我们的数据。

而右图是一个四次模型，过于拟合原数据，却没有很好的预测数据变化趋势。对于新的数据可能不能得到很好的效果。相比之下，中间的模型就很合适。

分类问题其实也是如此，

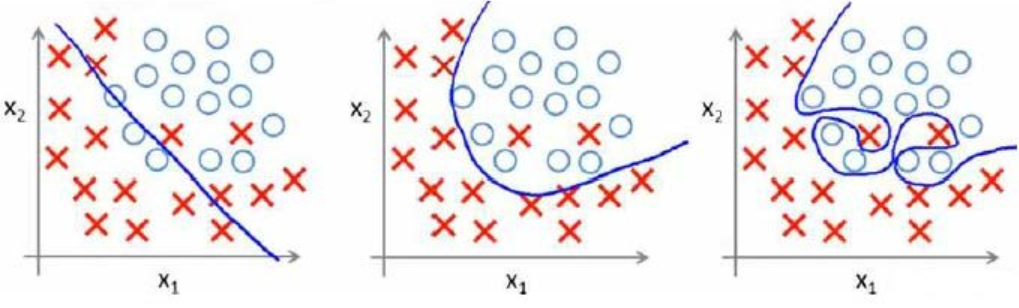
就以多项式理解，x的次数越高，拟合的越好，但相应的预测的能力就可能变差。

当发现模型过拟合时，该如何解决？

1 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如主成分分析法 PCA）

2 正则化。 保留所有的特征，但是减少参数的大小。

7.2 代价函数

  我们可以从之前的事例中看出，正是那些高次项导致了过拟合的产生，所以如果我们能让这些高次项的系数接近于0的话，我们就能很好的拟合了。这就是正则化的基本方法。我们要做的便是修改代价函数，对高次项的系数做惩罚项修改后的代价函数如下：

  假如我们有非常多的特征，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚。

7.3 正则化线性回归

正规化的线性回归与未正规化的类似，只是代价函数的计算发生了变化。

7.4 正则化的逻辑回归模型

针对逻辑回归，我们可以使用梯度下降法来优化代价函数。同样需要再代价函数里添加系数惩罚项：

       

虽然看上去它与线性回归一样，但是这里的h(x)是g(sita*X)，与线性回归并不完全相同。

高级的学习算法

第八、神经网络：表述(Neural Networks: Representation)

8.1 非线性假设

    无论是线性回归还是逻辑回归都有这样一个缺点，即：当特征太多时，计算的负荷会非常大。假设我们有非常多的特征，例如大于100个变量，我们希望用这100个特征来构建一个非线性的多项式模型，即便我们只采用两两特征的组合，我们也会有接近5000个组合而成的特征。这对于一般的逻辑回归来说需要计算的特征太多了。而对于图像我们会有更多的输入特征，普通的逻辑回归模型，不能有效地处理这么多的特征，这时候我们需要神经网络。

8.2 神经元和大脑

  神经网络逐渐兴起于二十世纪八九十年代，应用得非常广泛。但由于各种原因，在90年代的后期应用减少了。但是最近，神经网络又东山再起了。其中一个原因是：神经网络是计算量有些偏大的算法。然而大概由于近些年计算机的运行速度变快，才足以真正运行起大规模的神经网络。

8.3 模型表示1

神经网络模型是许多逻辑单元按照不同层级组织起来的网络，每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络，第一层成为输入层（Input Layer），最后一层称为输出层（Output Layer），中间一层成为隐藏层（Hidden Layers）。我们为每一层都增加一个偏差单位（bias unit）：

九、神经网络的学习(Neural Networks: Learning)

9.1需求预测

我们用四个特征（价格、运费、特定T恤的销量以及材料质量）来预测T恤的会畅销的概率，因此想通过构造神经元来实现此功能。

这四个特征  可能会影响三个因素 （可负担性，产品知名度，客户对产品的质量预期），进而影响畅销概率。

因此神经网络结构为： 四个输入，三个中间神经元，一个输出神经元。

但这些函数是我们手工制作的。

但我们知道的只有输入和输出，所以认为中间的层是隐藏的，我们看不到的。我们不知道会出现什么。

9.2 图像识别

一个1000*1000的图像，展开为向量后是一个维度为百万的特征向量，人脸识别的问题就是：能不能训练一个网络，以该特征向量为输入，识别图像中的人？

在训练好的人脸识别 神经网络中，可视化隐藏层参数发现：

    第一个隐藏层正在寻找低垂直线或垂直线边缘的神经元

    在早期的层中神经元再找非常短的线或者非常短的边缘。

  然后下一层的神经元，可能会学习将小短线和小短边组合到一起。

    最后将不同面部形状对应创建一组丰富的特征，然后通过输出层做预测。