ML——week2
4.1 多维特征
现在我们对房价模型增加更多的特征，例如房间数楼层等，构成一个含有多个变量的模型，模型中的特征为(x1,x2,x3,....,xn).
因此，用n表示特征的数量，用x(i)j 表示第i个实例的第j个特征。
则支持多变量的假设h可表示为：h(x(i))=sita0+sita1*x(i)1+sita2*x(i)2+...+sitan*x(i)n
4.2 多变量梯度下降
在多变量线性回归中，我们也构建一个代价函数，则这个代价函数是所有建模误差的平方和,即
则梯度下降算法为：
我们开始随机选择一系列的参数值，计算所有的预测结果后，再对所有的参数进行更新，如此循环直到收敛。
4.3 梯度下降法实践1-特征缩放
在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。例如在房屋预测中，房屋尺寸的值为 0-2000平方英尺，而房间数量的值则是0-5，因此我们希望将所以特征的尺度尽量统一一下。解决的办法是将其都缩放到-1到+1之间即可。
4.4 梯度下降法实践2-学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。当曲线趋于平缓，则说明算法开始收敛。
梯度下降算法的每次迭代受到学习率的影响，如果学习率过小，则达到收敛所需的迭代次数会非常高；如果学习率过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。
特征和多项式回归
线性的模型不一定适合所有的数据，因此有时我们需要选择曲线来适应数据，比如一个二次、三次或者更高次的模型。通常可以先观察数据，然后再决定尝试哪种模型。在使用多项式模型时，特征缩放十分有必要。
正规方程
到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法是更好的解决方案。如果代价函数是个二次函数：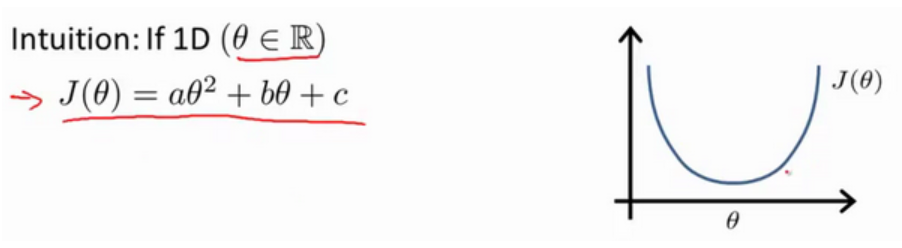 
则使得该代价函数最小的参数值可以根据正规方程的性质直接求出：sita=(XT X)-1 XT y.
但是这种方法是有适用范围的：对于不可逆的矩阵（特征之间不独立，或者特征数大于训练样本数），该方法不可用。
正规方程的实现
import numpy as np
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X)
return theta正规方程及不可逆性（可选）
在Octave里，有两个函数可以求解矩阵的逆，一个被称为pinv()，另一个是inv()，这两者之间的差异是些许计算过程上的，一个是所谓的伪逆，另一个被称为逆。使用pinv() 函数可以展现数学上的过程，这将计算出XTX的值，即便矩阵是不可逆的。
如果遇到XTX是奇异矩阵，则我们可以这样做：首先，看特征值里是否有一些多余的特征，像这些x1和x2是线性相关的。同时，当有一些多余的特征时，可以删除这两个重复特征里的其中一个，无须两个特征同时保留，将解决不可逆性的问题。如果矩阵是不可逆的，（通常来说，不会出现这种情况），如果在Octave里，可以用伪逆函数pinv() 来实现。这种使用不同的线性代数库的方法被称为伪逆。即使的结果是不可逆的，但算法执行的流程是正确的。
逻辑回归(Logistic Regression)
6.1 分类问题
在分类问题中，你要预测的变量不再是连续的值，而是离散的值，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前最流行使用最广泛的一种学习算法。
在分类问题中，我们尝试预测的是结果是否属于某一个类（例如正确或错误）。分类问题的例子有：判断一封电子邮件是否是垃圾邮件；判断一次金融交易是否是欺诈；之前我们也谈到了肿瘤分类问题的例子，区别一个肿瘤是恶性的还是良性的。
首先关注二元的分类问题，我们希望将输出控制在0-1之间，并以0.5将输出分为两类。
6.2 假说表示
在分类问题中，要用什么样的函数来表示我们的假设。此前我们说过，希望我们的分类器的输出值在0和1之间，因此，我们希望想出一个满足某个性质的假设函数，这个性质是它的预测值要在0和1之间。
如果这里继续使用线性回归，遇到较大的X时输出y就可能会越界，而且对于0.5附近的输出其分类也并不具有说服力。因此引入新的模型，就叫做逻辑回归。该模型的输出变量范围始终在0和1之间。 逻辑回归模型的假设是：
h(x)=g(sita*x) , 这里的g是一个逻辑函数（Sigmoid function）
该函数的图像为：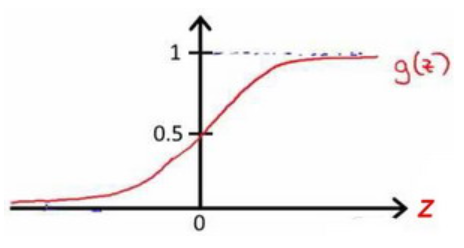 
因此可以看出，该函数将R映射到（0,1）上，从而保证了函数输出的范围。
6.3 判定边界
判定边界或者说，决策边界(decision boundary)的概念：在二元决策时一般认为sigmoid函数值大于0.5时，y=1；当值小于0.5时，y=0.
而令sigmoid函数等于0.5，即令z=0的输入X，属于决策的边界。所以这样所有的x所构成的即为决策边界。
6.4 代价函数
要衡量选定模型后，相应参数对数据的拟合程度，要定义用来拟合参数的优化目标或者叫代价函数，这便是监督学习问题中的逻辑回归模型的拟合问题。
对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将sigmoid函数带入平方差损失时，得到的是一个非凸函数，有着多个局部最小值，影响梯度下降的效果。
因此需要重新定义逻辑回归的代价函数
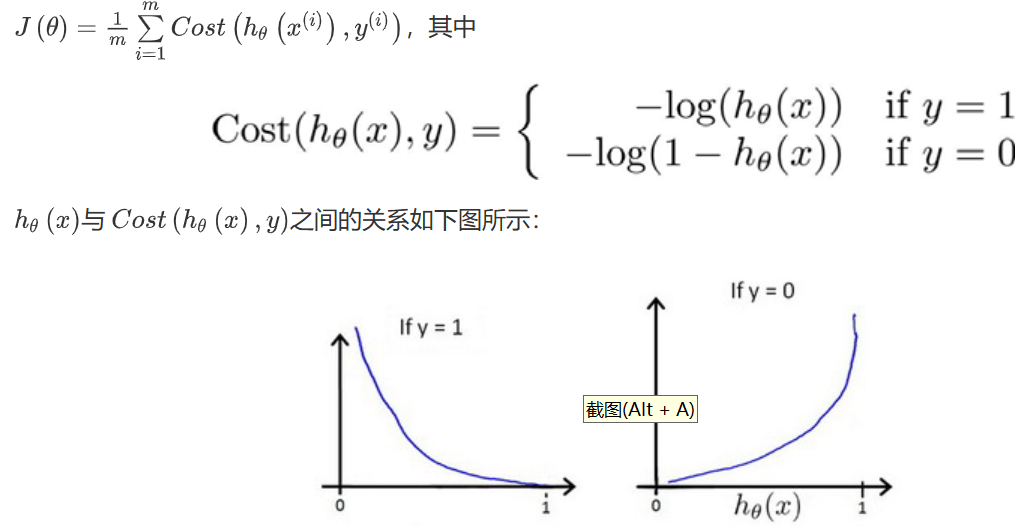
这样的凸函数的优化问题可以使用梯度下降轻松实现。更新算法如下：
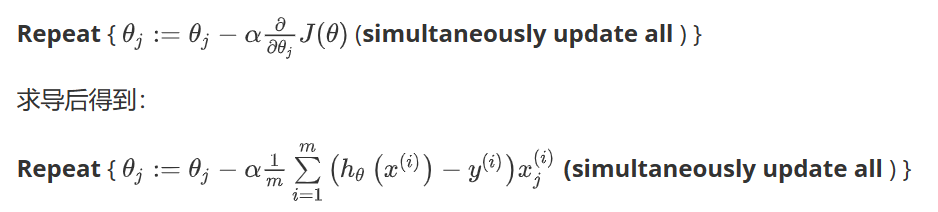
一些梯度下降算法之外的选择： 除了梯度下降算法以外，还有一些常被用来令代价函数最小的算法，这些算法更加复杂和优越，而且通常不需要人工选择学习率，通常比梯度下降算法要更加快速。这些算法有：共轭梯度（Conjugate Gradient），局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)
6.5 简化的成本函数和梯度下降
对于逻辑回归，我们希望简写代价函数，并运用梯度下降，来拟合逻辑回归的参数。
化简该函数，可以得到：
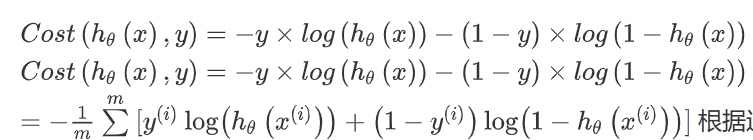
为了找到另J(sita)尽可能小的参数，我们采用梯度下降法。
6.6 高级优化
本届将学习一些高级优化算法和一些高级的优化概念，利用这些方法，我们就能够使通过梯度下降，进行逻辑回归的速度大大提高，而这也将使算法更加适合解决大型的机器学习问题，比如，我们有数目庞大的特征量。
对于梯度下降，我们的目标是最小化代价函数J（sita），对于输入的sita，我们会计算J（sita），以及J对于每个参数的偏导。 然后我们需要做的就是：
当我们构建完成以上功能的函数后，梯度下降就是不断重复以上步骤。
然而梯度下降并不是我们可以使用的唯一算法。共轭梯度法 BFGS (变尺度法) 和L-BFGS (限制变尺度法) 就是其中一些更高级的优化算法，它们需要有一种方法来计算 ，以及需要一种方法计算导数项，然后使用比梯度下降更复杂的算法来最小化代价函数。
6.7 多类别分类：一对多
此前我们一直在讨论二元的分类问题，在二元分类问题中，两个分类是非此即彼的关系。但是有时分类问题可能会有多个选项。
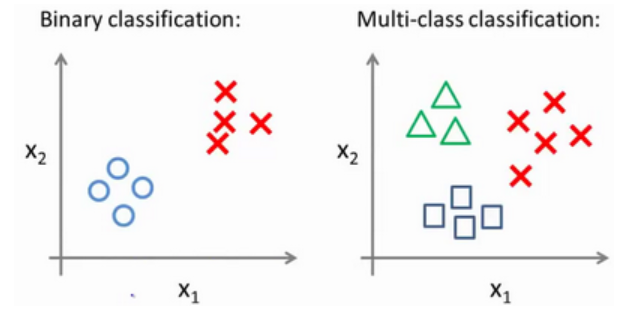
下面将介绍如何进行一对多的分类工作，有时这个方法也被称为"一对余"方法。现在我们有一个训练集，好比上图表示的有3个类别，我们下面要做的就是使用一个训练集，将其分成3个二元分类问题。
我们先从用三角形代表的类别1开始，实际上我们可以创建一个，新的"伪"训练集，类型2和类型3定为负类，类型1设定为正类，我们创建一个新的训练集，如下图所示的那样，我们要拟合出一个合适的分类器。
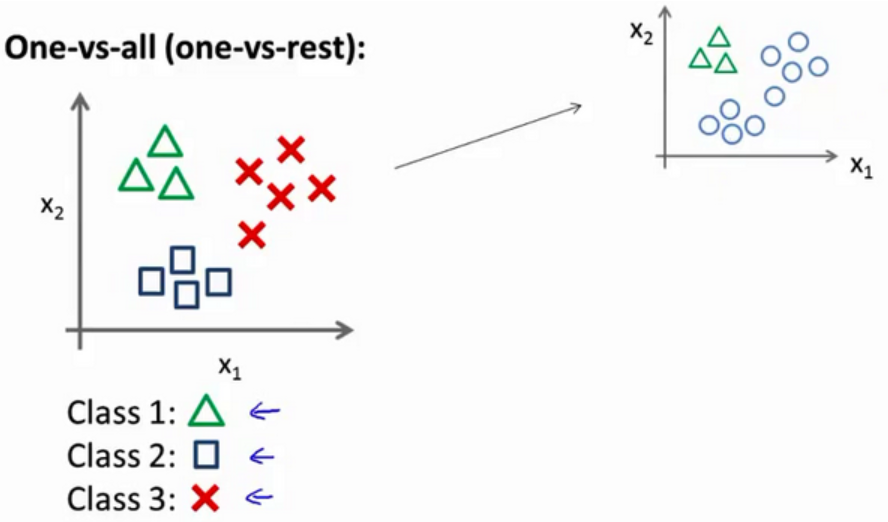
重复三次以上过程，可以得到三个分类机。最后，在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量。
