ML-week1

1.2 机器学习是什么？

Arthur Samuel：他定义机器学习为，在进行特定编程的情况下，给予计算机学习能力的领域。

Tom(卡内基梅隆大学)定义的机器学习是，一个好的学习问题定义如下，一个程序被认为能从经验E中学习，解决任务T，达到性能度量值P，当且仅当有了经验E后，经过P评判，程序在处理T时的性能有所提升。

机器学习主要有两种类型的算法：我们称之为监督学习和无监督学习。

1.3 监督学习

  监督学习指的就是我们给学习算法一个包含正确答案数据集，根据数据集学习所给的数据特征与正确答案的关系。可以是分类问题，也可以是回归问题。

1.4 无监督学习

  无监督学习的数据集中没有任何的标签。其中一个无监督学习就是对数据集进行聚类，也称聚类算法。

最后介绍了一个工具：Octave

2.1 模型表示

本节将通过线性回归来了解监督学习的过程:

对于房价预测模型，我们之所以将其称为监督学习（因为对每个数据都有一个正确答案-真实的房价）。由于房价是一些连续的值，因此这是一个回归问题。

 h代表学习算法的解决方案或函数也称为假设（hypothesis）,监督学习算法的工作方式如下

        

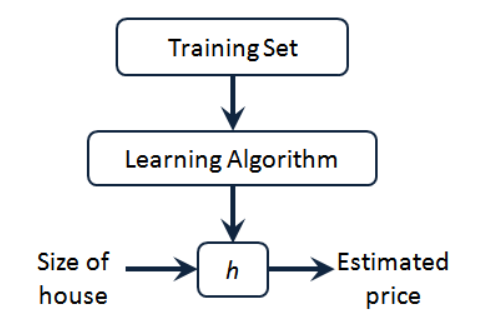
要解决房价预测问题，我们实际上是要将训练集“喂”给我们的学习算法，进而学习得到一个假设h，然后将我们要预测的房屋的尺寸作为输入变量输入给h，预测出该房屋的交易价格作为输出变量输出为结果。那么，对于我们的房价预测问题，我们该如何表达h？

  一种可能的表达是h(x)=ax+b,因为只有一个特征/输入变量，因此称其为单变量线性回归。

2.2 代价函数

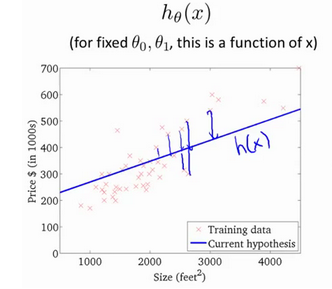
  在假设函数h(x)=ax+b中，我们将a,b称为模型参数。我们希望为模型选择合适的参数（parameters），我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是建模误差（modeling error）。

          

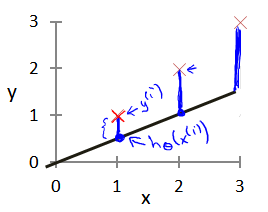
  为了准确的衡量建模误差的大小，用代价函数J(a,b)来表示（这里是平方差公式）

                 

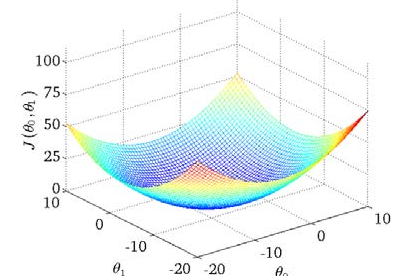
    通过这个三位图像可以看到J(a,b)函数值随自变量的变化情况。我们希望从中找到一组(a,b)使得函数值J(a,b)

2.3 代价函数的直观理解I

在上一个视频中，我们给了代价函数一个数学上的定义。在这个视频里，  让我们通过一些例子来获取一些直观的感受，看看代价函数到底是在干什么。

            

2.4 代价函数的直观理解II

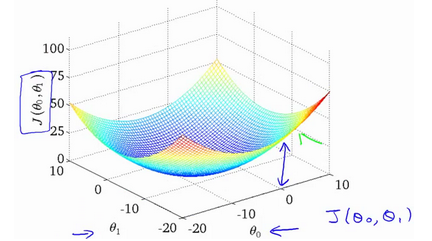
我们将更深入地学习代价函数的作用.左侧是代价函数，右侧是模型。我们训练模型的过程，其实就是不断移动参数(a,b),从而让模型中真实值和预测值直接的差距尽可能小。我们不能总手动解，因此我们真正需要的是编写程序来找出这些最小化代价函数的和的值。

        .

2.5 梯度下降

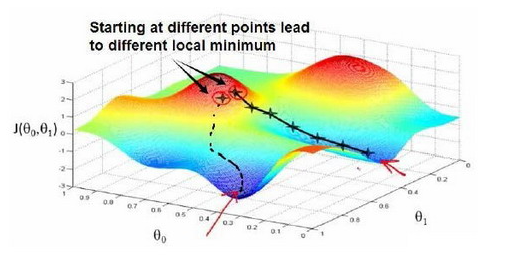
  梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数 的最小值.开始时我们随机选择一个参数的组合，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

          

  在需要更新参数的时候，我们需要根据前一步的结果同时更新下一步的所有参数，同时更新是梯度下降中的一种常用方法。我们之后会讲到，同步更新是更自然的实现方法。(如下图所示)

      

2.6 梯度下降的直观理解

  梯度下降的公式为通过对sita使得按梯度下降最快方向进行，一直迭代下去，最终得到局部最小值。arfa是学习率，它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

  如果arfa太小了，即我的学习速率太小，那就只能在图像上小步移动，最终需要很多步才能到达最低点。

  如果arfa太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛。下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远。  

  当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，这是因为当我们接近局部最低点时，很显然在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。所以实际上没有必要再另外减小。

2.7 梯度下降的线性回归

  我们要将梯度下降和代价函数结合，应用于具体的拟合直线的线性回归算法里。

  如图所示，代价函数的梯度表示为：

        

这个算法有时候也叫批量梯度下降。”批量梯度下降”，指的是在梯度下降的每一步中，我们都用到了所有的训练样本，在梯度下降中，在计算微分求导项时，我们需要进行求和运算，所以，在每一个单独的梯度下降中，需要对所有个训练样本求和。

3.1 矩阵和向量

这一节对矩阵和向量的概念进行描述，不再赘述。

3.2 加法和标量乘法

矩阵和矩阵的加法：对应元素相加

矩阵和标量乘法：矩阵的每个元素都与标量相乘

3.3 矩阵向量乘法    以及  3.4 矩阵乘法

都可以看作是矩阵乘法，第i行乘第j列，对应元素相乘再相加，然后放到结果矩阵的第i行第j列元素。

3.5 矩阵乘法的性质

矩阵乘法不满足交换律: A*B不等于B*A

矩阵乘法满足集合律: (A*B)*C=A*(B*C)

主对角线上元素为1，其他元素为0的矩阵是单位矩阵。

3.6 逆、转置

对于一个m*m 的方阵A，如果存在矩阵B，使得A*B=B*A=E，则称B为A的逆矩阵。

我们一般在OCTAVE或者MATLAB中进行计算矩阵的逆矩阵。

转置是指，对于一个n*m的矩阵A，它的转置矩阵B(m*n)表示为b(i,j)=a(j,i)