AI-11. 优化算法
优化算法对于深度学习非常重要。一方面,训练复杂的深度学习模型可能需要数小时、几天甚至数周。优化算法的性能直接影响模型的训练效率。另一方面,了解不同优化算法的原则及其超参数的作用将使我们能够以有针对性的方式调整超参数,以提高深度学习模型的性能。
11.1. 优化和深度学习
对于深度学习问题,我们通常会先定义损失函数。一旦我们有了损失函数,我们就可以使用优化算法来尝试最小化损失。在优化中,损失函数通常被称为优化问题的目标函数。尽管优化提供了一种最大限度地减少深度学习损失函数的方法,但本质上,优化和深度学习的目标是根本不同的。前者主要关注的是最小化目标,后者则关注在给定有限数据量的情况下寻找合适的模型。
深度学习优化存在许多挑战。其中最令人烦恼的是局部最小值、鞍点和梯度消失。
局部最优:通过最终迭代获得的数值解可能仅使目标函数局部最优,而不是全局最优。只有一定程度的噪声可能会使参数跳出局部最小值。事实上,这是小批量随机梯度下降的有利特性之一。在这种情况下,小批量上梯度的自然变化能够将参数从局部极小值中跳出。
鞍点:鞍点(saddle point)是指函数的所有梯度都消失但既不是全局最小值也不是局部最小值的任何位置。
梯度消失:某些函数会出现梯度很小的情况,例如tanh(x)在x非常大时梯度非常小,
练习:
1考虑一个简单的MLP,它有一个隐藏层,比如,隐藏层中维度为d和一个输出。证明对于任何局部最小值,至少有d!个等效方案。
2假设我们有一个对称随机矩阵M,其中条目Mij=Mji各自从某种概率分布pij中抽取。此外,假设pij(x)=pij(−x),即分布是对称的(详情请参见 (Wigner, 1958))。
证明特征值的分布也是对称的。也就是说,对于任何特征向量v,关联的特征值λ满足P(λ>0)=P(λ<0)的概率为P(λ>0)=P(λ<0)。为什么以上没有暗示P(λ>0)=0.5?
3假设你想在(真实的)鞍上平衡一个(真实的)球。为什么这很难?能利用这种效应来优化算法吗?
虽然鞍点处其导数为0,但是总存在较高的一侧和较低的一侧,球总是从较低的一侧落下。动量法?
11.2. 凸性
凸 集(convex set)是凸性的基础。 简单地说,如果对于任何a,b∈X,连接a和b的线段也位于X中,则向量空间中的一个集合X是凸(convex)的。有了凸集可定义凸函数。
给定一个凸函数f,最有用的数学工具之一就是詹森不等式(Jensen’s inequality)。 它是凸性定义的一种推广:换句话说,凸函数的期望不小于期望的凸函数。
凸函数还有很多很好的性质和定理,便于我们进行优化。
练习:
1假设我们想要通过绘制集合内点之间的所有直线并检查这些直线是否包含来验证集合的凸性。i.证明只检查边界上的点是充分的。ii.证明只检查集合的顶点是充分的。
答:集合A中任一点u都可以由边界上点来表示u=x1*k1+y1*(1-k1),v=x2*k2+y2*(1-k2) ,则线段u-v上的点都可以由边界上的点来表示,只要边界上点满足,整个集合满足。
答:边界上得点可以由定点表示,定点满足,则边界满足,则全集合满足。
2用p-范数表示半径为:r的球,证明Bp[r]:={x|x∈Rd and ‖x‖p≤r},Bp[r]对于所有p≥1是凸的。
3已知凸函数f和g表明max(f,g)也是凸函数。证明min(f,g)是非凸的。
4证明Softmax函数的规范化是凸的,即f(x)=log∑iexp(xi)的凸性。
5证明线性子空间X={x|Wx=b}是凸集。
6证明在线性子空间b=0的情况下,对于矩阵M的投影ProjX可以写成MX。
7证明对于凸二次可微函数f,对于ξ∈[0,ϵ],我们可以写成f(x+ϵ)=f(x)+ϵf′(x)+12ϵ2f″(x+ξ)。
8给定一个凸集X和两个向量x和y证明了投影不会增加距离,即‖x−y‖≥‖ProjX(x)−ProjX(y)‖。

11.3. 梯度下降
一维梯度下降的过程,就是通过泰勒展开,使函数朝导数方向移动。对于多元函数梯度下降仍然适用。
学习率(learning rate)决定目标函数能否收敛到局部最小值,以及何时收敛到最小值。
如果我们把它选得太小,就没有什么进展;如果太大,得到的解就会振荡。 如果我们可以自动确定学习率,或者完全不必选择学习率,会怎么样? 除了考虑目标函数的值和梯度、还考虑它的曲率的二阶方法可以帮我们解决这个问题。 虽然由于计算代价的原因,这些方法不能直接应用于深度学习,但它们为高级优化算法提供了有用的思维。
练习:
1用不同的学习率和目标函数进行梯度下降实验。
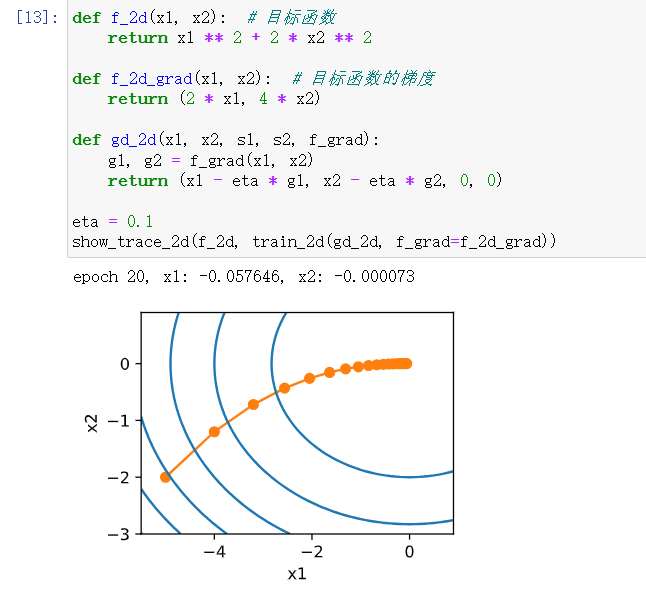
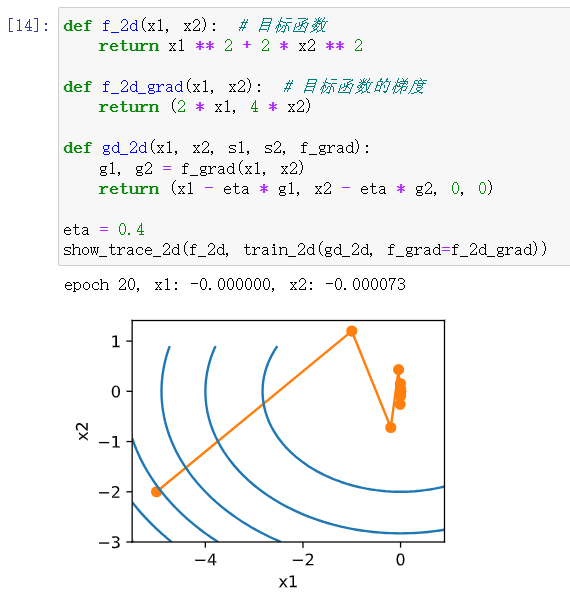
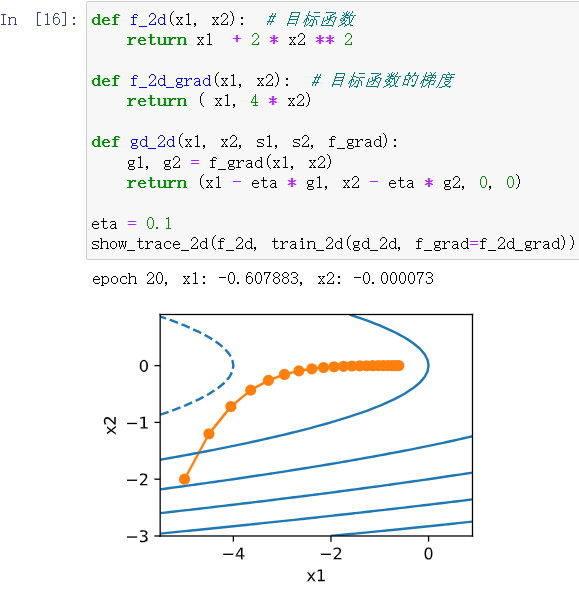
2设计一个定义在R2上的目标函数,它的梯度下降非常缓慢。提示:不同坐标的缩放方式不同。
f(x1,x2)=log(x1+10)+log(x2+10) 导数小的函数?
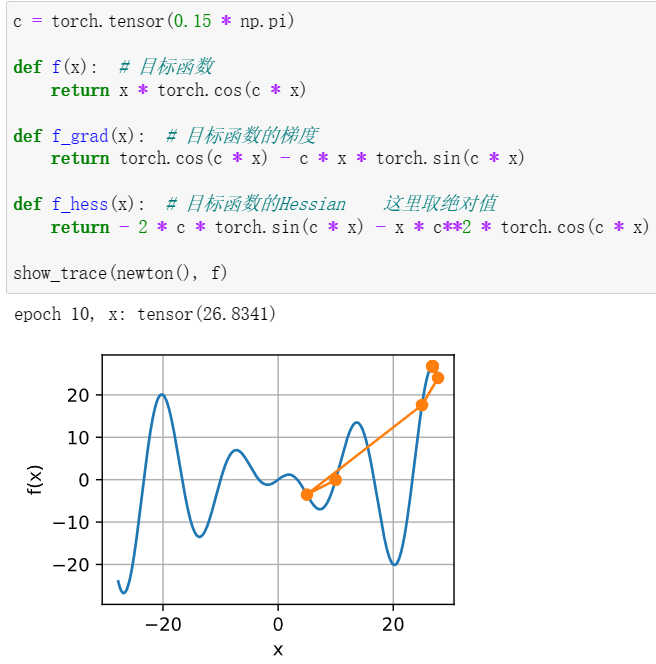
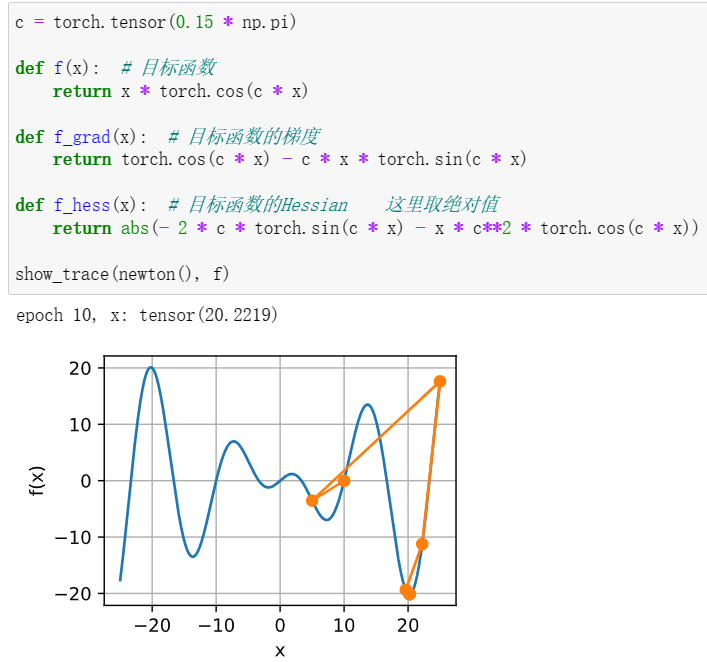
3使用预处理实现牛顿方法的轻量版本。
使用对角Hessian作为预条件子。使用它的绝对值,而不是实际值(可能有符号)。将此应用于上述问题。
左-直接使用海森矩阵 右-使用海森的绝对值(效果明显提升)
11.4. 随机梯度下降
如果使用梯度下降法,则每个自变量迭代的计算代价为O(n),它随n线性增长。因此,当训练数据集较大时,每次迭代的梯度下降计算代价将较高。随机梯度下降(SGD)可降低每次迭代时的计算代价。在随机梯度下降的每次迭代中,我们对数据样本随机均匀采样一个索引i,其中i∈{1,…,n},并计算梯度以更新x:
用与时间相关的学习率(t)取代增长率增加了控制优化算法收敛的复杂性。
常用的几个方法是:分段常数,指数衰减,多项式衰减。一个受欢迎的选择是指数为0.5的多项式衰减(polynomial decay)。在凸优化的情况下,有许多证据表明这种速率表现良好。
练习:

1改变迭代次数,和最优解的距离反而越来越远。
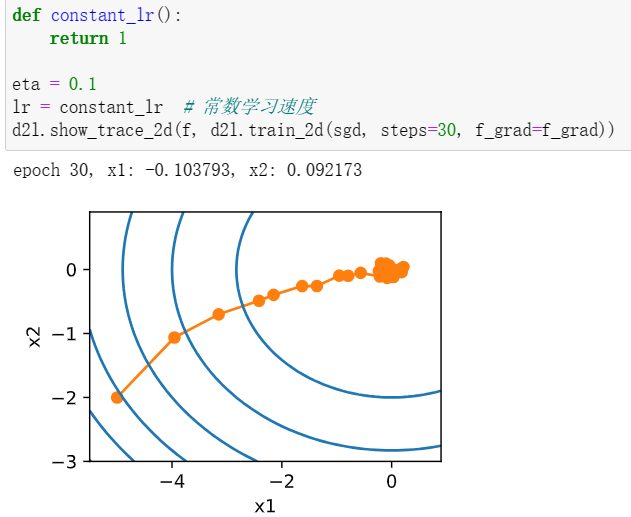
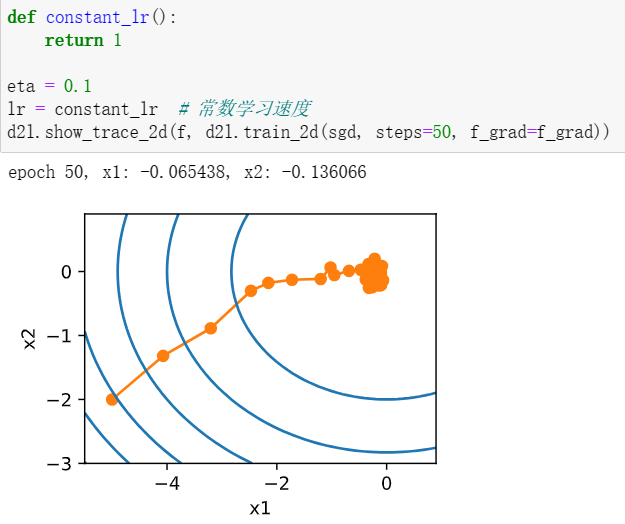
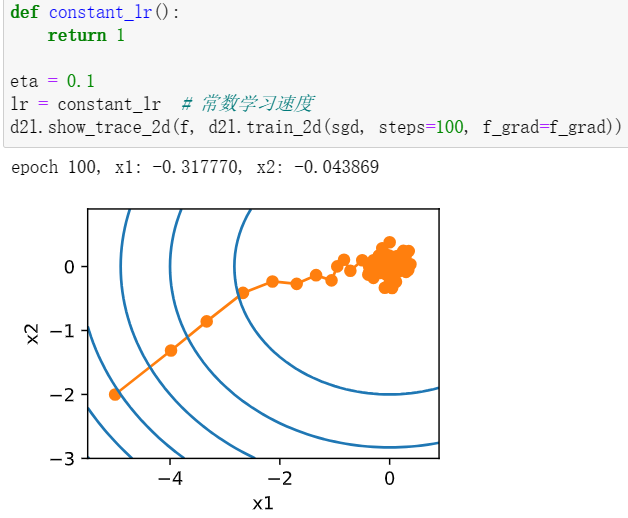
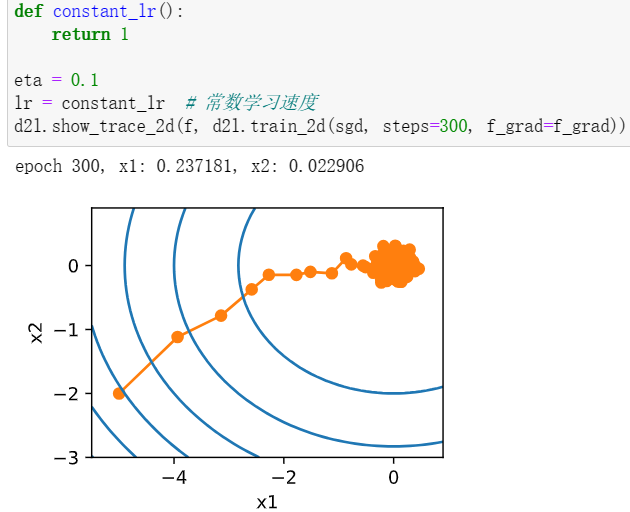
2显然,添加噪声后的f即为所证,w即为噪声
3无替换的下降速率更快
4可以使用动量法,没必要只依靠其梯度
11.5. 小批量随机梯度下降
在梯度下降和随机梯度下降之前进行了一个权衡,使用小批量数据进行随机梯度下降。
小批量随机梯度下降的原因:
- 当样本数据较多时,若将所有样本同时进行计算,则缓存开销巨大,而每次适当缩小样本数量可以缓解此问题。
- 适量多的样本在GPU等高性能运算器中并行运算可以提高运行效率。
在小批量随机梯度下降中,我们处理通过训练数据的随机排列获得的批量数据(即每个观测值只处理一次,但按随机顺序)。
def train_sgd(lr, batch_size, num_epochs=2):
data_iter, feature_dim = get_data_ch11(batch_size)
return train_ch11(
sgd, None, {'lr': lr}, data_iter, feature_dim, num_epochs)比较三种梯度下降法的优劣
gd_res = train_sgd(1, 1500, 10)#梯度下降
sgd_res = train_sgd(0.005, 1)#随机梯度
mini1_res = train_sgd(.4, 100)#小批次
mini2_res = train_sgd(.05, 10)#小批次2接下来,绘图
d2l.set_figsize([6, 3])
d2l.plot(*list(map(list, zip(gd_res, sgd_res, mini1_res, mini2_res))),
'time (sec)', 'loss', xlim=[1e-2, 10],
legend=['gd', 'sgd', 'batch size=100', 'batch size=10'])
d2l.plt.gca().set_xscale('log')
练习:
1修改批量大小和学习率,并观察目标函数值的下降率以及每个迭代轮数消耗的时间。
学习率大的时候,可能会发生发散情况,每轮迭代消耗的时间也会增加。
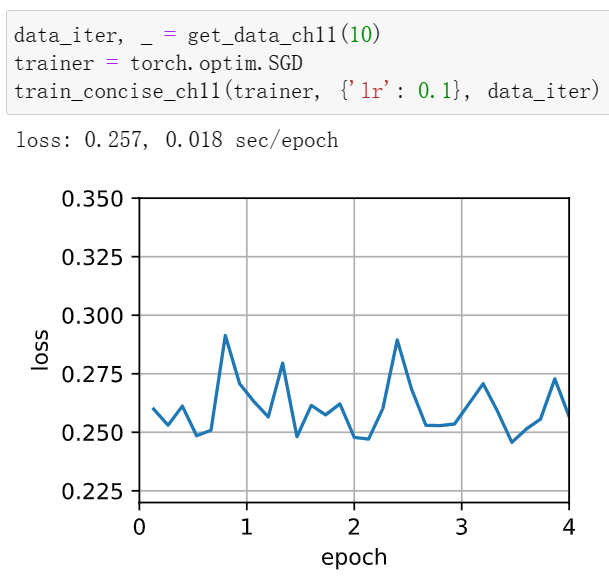
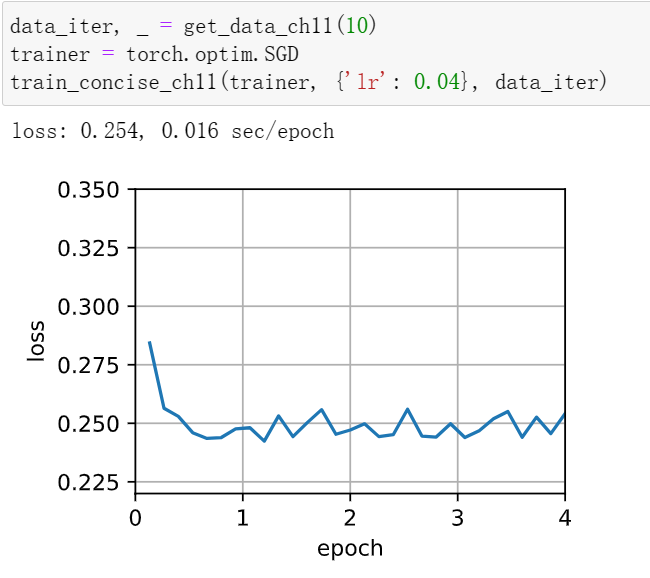
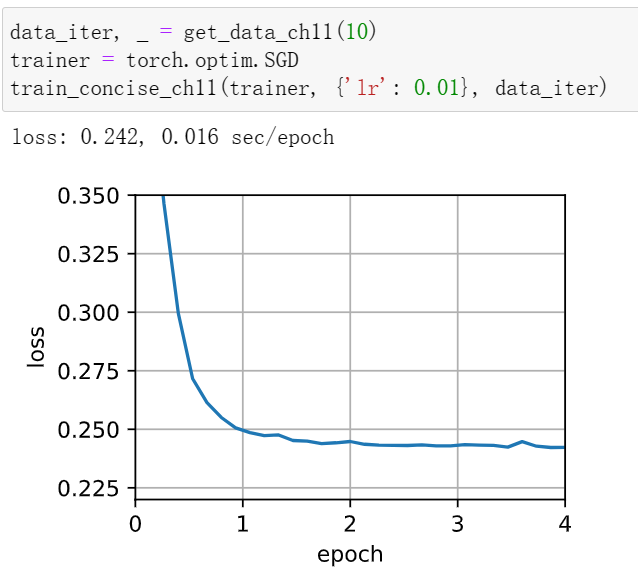
11.6. 动量法
动量法的思路是将瞬时梯度替换为多个“过去”梯度的平均值。 𝐯被称为动量(momentum), 它累加了过去的梯度。
由于对过去的数据进行了指数降权,有效梯度数为1/(1-lambda)。距离越远的梯度,在动量中的权重越小。
练习:
1使用动量超参数和学习率的其他组合,观察和分析不同的实验结果。
学习率减小后收敛效果变好,动量超参数减小后收敛的更快了(但训练时间变长,计算量大)
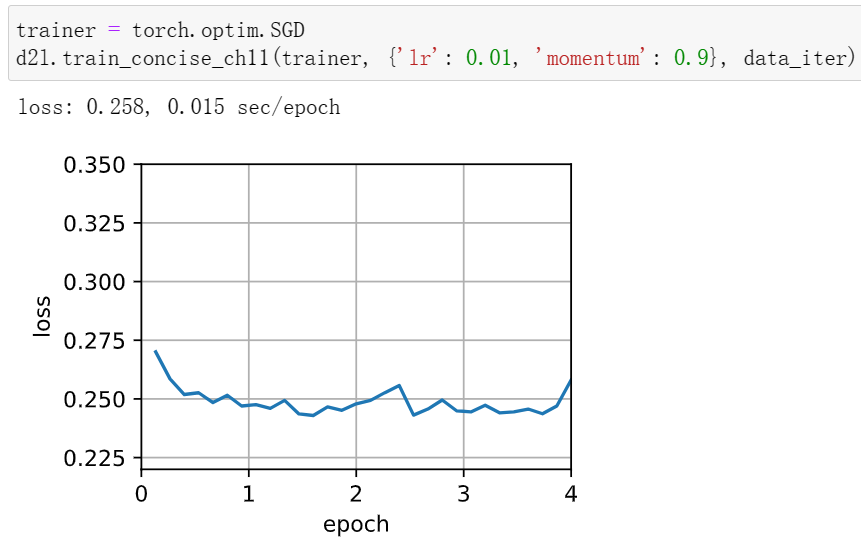
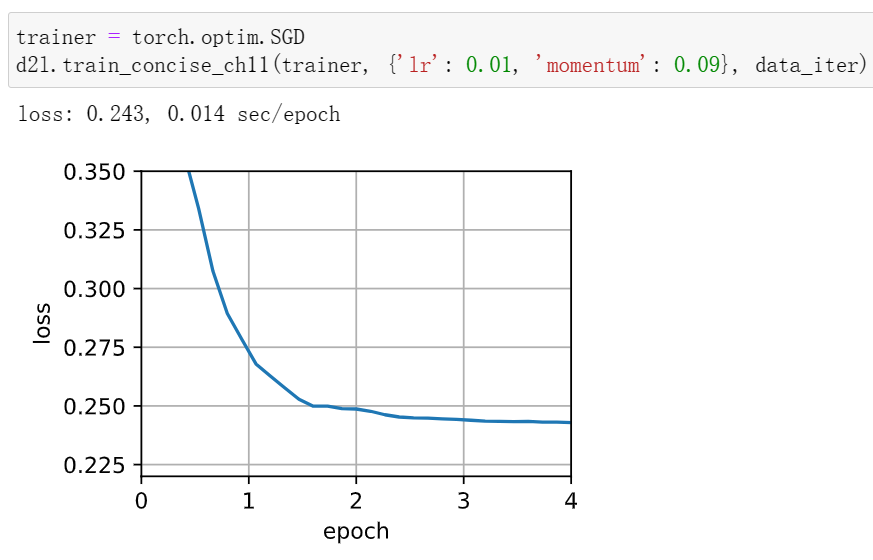
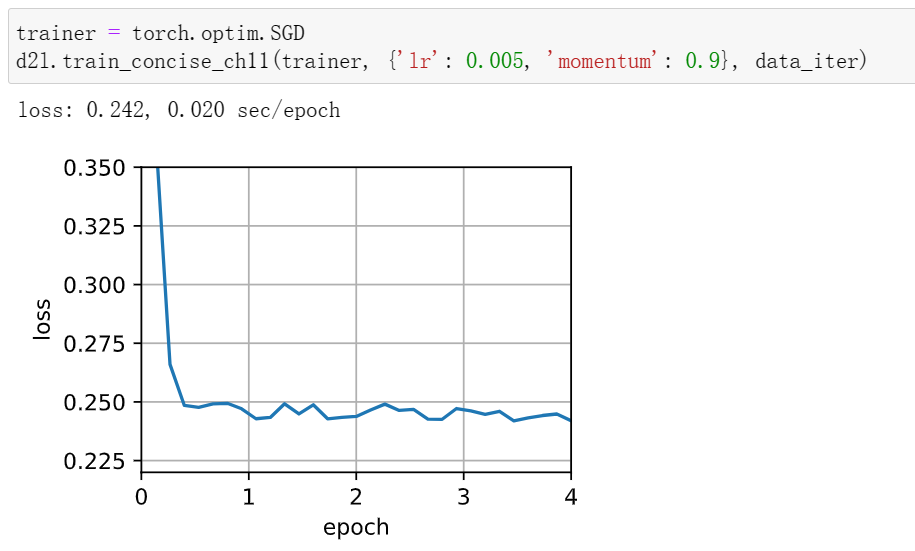
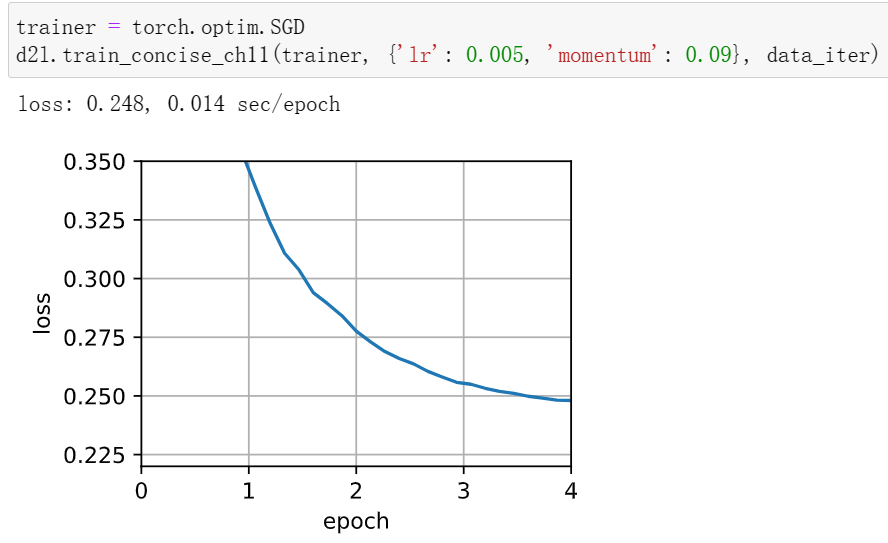

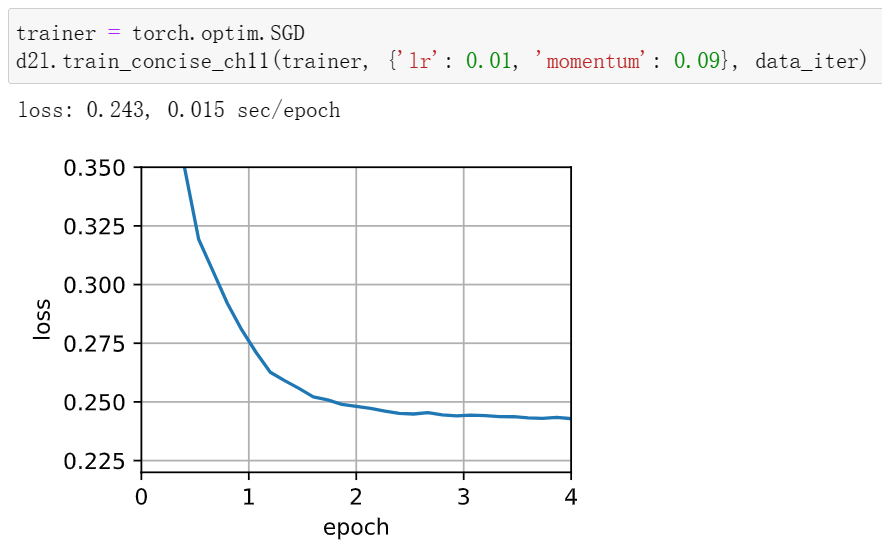
2当我们执行带动量法的随机梯度下降时会有什么变化?当我们使用带动量法的小批量随机梯度下降时会发生什么?试验参数如何?
随机梯度下降
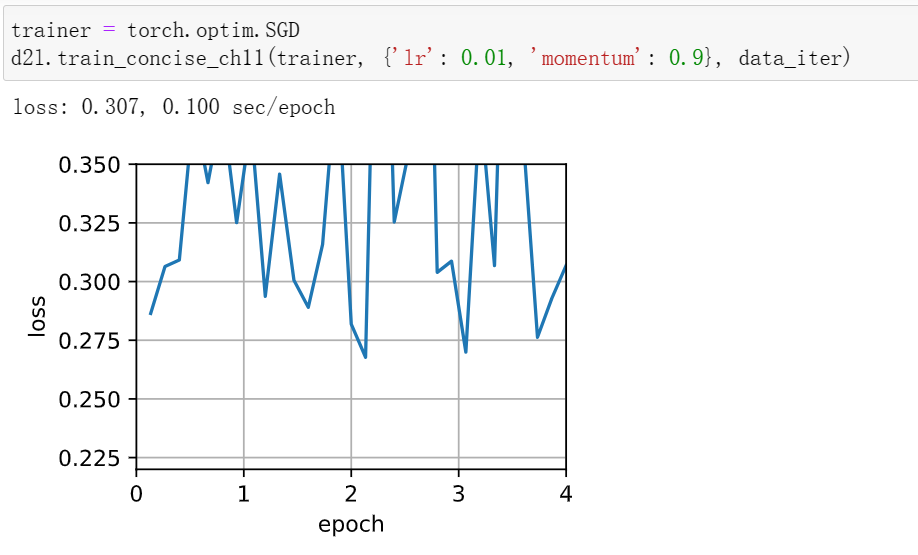
小批量随机梯度
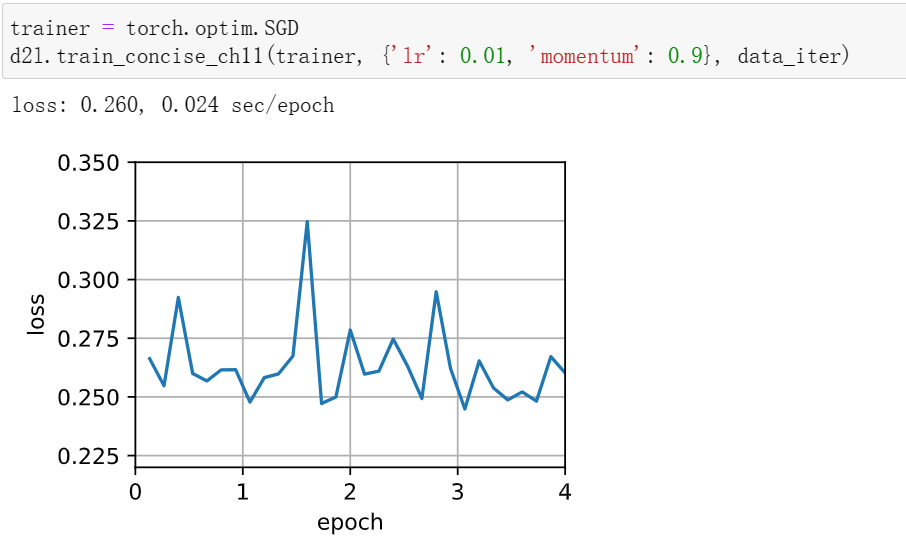
AdaGrad算法:
关于稀疏特征(即只在偶尔出现的特征)的模型训练,某些特征常见,某些特征不常见,常见特征的参数相当迅速地收敛到最佳值,而对于不常见的特征,我们仍缺乏足够的观测以确定其最佳值。解决此问题的一个方法是记录我们看到特定特征的次数,然后将其用作调整学习率。
Adadelta算法:
Adadelta没有学习率参数。相反,它使用参数本身的变化率来调整学习率。
RMSProp算法:
Adagrad算法将梯度的平方累加成状态矢量,RMSProp算法则将其修改为泄露平均值
Adam算法:
Adam算法将许多优化算法的功能结合到了相当强大的更新规则中,它使用指数加权移动平均值来估算梯度的动量和二次矩。
11.11. 学习率调度器
调整学习率通常与实际算法同样重要,有如下几方面需要考虑:
- 学习率的大小
- 学习率的衰减速度
- 如何初始化
常用的策略包括:多项式衰减和分段常数表。 此外,余弦学习率调度在实践中的一些问题上运行效果很好。 在某些问题上,最好在使用较高的学习率之前预热优化器。
预热:
在某些情况下,初始化参数不足以得到良好的解。 这对某些高级网络设计来说尤其棘手,可能导致不稳定的优化结果。 对此,一方面,我们可以选择一个足够小的学习率, 从而防止一开始发散,然而这样进展太缓慢。 另一方面,较高的学习率最初就会导致发散。
解决这种困境的一个相当简单的解决方法是使用预热期,在此期间学习率将增加至初始最大值,然后冷却直到优化过程结束。 为了简单起见,通常使用线性递增。
练习:
-
试验给定固定学习率的优化行为。这种情况下可以获得的最佳模型是什么?
-
如果改变学习率下降的指数,收敛性会如何改变?在实验中方便起见,使用
PolyScheduler。 -
将余弦调度器应用于大型计算机视觉问题,例如训练ImageNet数据集。与其他调度器相比,它如何影响性能?
-
预热应该持续多长时间?



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 如何调用 DeepSeek 的自然语言处理 API 接口并集成到在线客服系统
· 【译】Visual Studio 中新的强大生产力特性
· 2025年我用 Compose 写了一个 Todo App