AI-6卷积神经网络

6.1从全连接层到卷积层

之前的多层感知机，仅仅通过将图像数据展平成一维向量而忽略了每个图像的空间结构信息。

卷积神经网络则改善了这一点，且卷积神经网络需要的参数少于全连接架构的网络同时卷积也很容易用GPU并行计算，因此更适合于高效的进行计算。

练习

1假设卷积层 (6.1.3)覆盖的局部区域Δ=0。在这种情况下，证明卷积内核为每组通道独立地实现一个全连接层。

验证代码

# 代码验证
import torch
import torch.nn as nn

#全连接层
class MyNet1(nn.Module):
    def __init__(self, linear1, linear2):
        super(MyNet1, self).__init__()
        self.linear1 = linear1
        self.linear2 = linear2

    def forward(self, X):
        return self.linear2(self.linear1(nn.Flatten()(X)))

#1x1 的卷积层
class MyNet2(nn.Module):
    def __init__(self, linear, conv2d):
        super(MyNet2, self).__init__()
        self.linear = linear
        self.conv2d = conv2d

    def forward(self, X):
        X = self.linear(nn.Flatten()(X))
        X = X.reshape(X.shape[0], -1, 1, 1)
        X = nn.Flatten()(self.conv2d(X))
        return X


linear1 = nn.Linear(15, 10)
linear2 = nn.Linear(10, 5)
conv2d = nn.Conv2d(10, 5, 1)

linear2.weight = nn.Parameter(conv2d.weight.reshape(linear2.weight.shape))
linear2.bias = nn.Parameter(conv2d.bias)

net1 = MyNet1(linear1, linear2)
net2 = MyNet2(linear1, conv2d)

X = torch.randn(2, 3, 5)
# 两个结果实际存在一定的误差，直接print(net1(X) == net2(X))得到的结果不全是True
print(net1(X))
print(net2(X))

tensor([[ 0.1889,  0.3318,  0.3985, -0.1788, -0.3390],
        [-0.2068,  0.2603, -0.5014,  0.7563, -0.4728]],
       grad_fn=<AddmmBackward0>)
tensor([[ 0.1889,  0.3318,  0.3985, -0.1788, -0.3390],
        [-0.2068,  0.2603, -0.5014,  0.7563, -0.4728]],
       grad_fn=<ReshapeAliasBackward0>)

2为什么平移不变性可能也不是好主意呢？

平移不变性可能会降低模型的准确性和泛化能力。对于某些任务，平移不变性并不是必须的特性。例如，对于图像分类任务，我们通常希望模型能够识别物体的位置和姿态，并根据这些信息对其进行分类。

3当从图像边界像素获取隐藏表示时，我们需要思考哪些问题？

需要考虑填充多大的padding的问题

4描述一个类似的音频卷积层的架构。

卷积神经网络（CNN）是深度学习中常用的网络架构，在智能语音中也不例外，比如语音识别。语音中是按帧来处理的，每一帧处理完就得到了相对应的特征向量，常用的特征向量有MFCC等，通常处理完一帧得到的是一个39维的MFCC特征向量。假设一段语音有N帧，处理完这段语音后得到的是一个39行N列（行表示特征维度，列表示帧数）的矩阵，这个矩阵是一个平面，是CNN的输入。应用在图像问题上的CNN通常是二维卷积（因为图像有RGB三个通道），而语音问题上的CNN输入是一个矩阵平面，可以用一维卷积。所谓一维卷积是指卷积核只在一个方向上移动。具体到语音上，假设一段语音提取特征后是一个M行N列（M表示特征维度，N表示帧数）的矩阵平面，卷积核要在帧的方向上从小到大移动。

原文链接：https://blog.csdn.net/david_tym/article/details/112756785

5卷积层也适合于文本数据吗？为什么？

卷积层也适合于文本数据。在自然语言处理中，文本数据通常表示为词向量矩阵，其中每行代表一个词的向量表示。卷积层可以在这个矩阵上进行卷积操作。此外，卷积层还可以与循环神经网络结合使用，形成卷积神经网络和循环神经网络的混合模型。这种模型可以同时捕捉文本中的局部特征和全局特征，提高模型的性能。

.2图像卷积

在卷积神经网络中，对于某一层的任意元素x，其感受野（receptive field）是指在前向传播期间可能影响x计算的所有元素（来自所有先前层）。

练习

构建一个具有对角线边缘的图像X。
1. 如果将本节中举例的卷积核K应用于X，会发生什么情况？
2. 如果转置X会发生什么？
3. 如果转置K会发生什么？
在我们创建的Conv2D自动求导时，有什么错误消息？
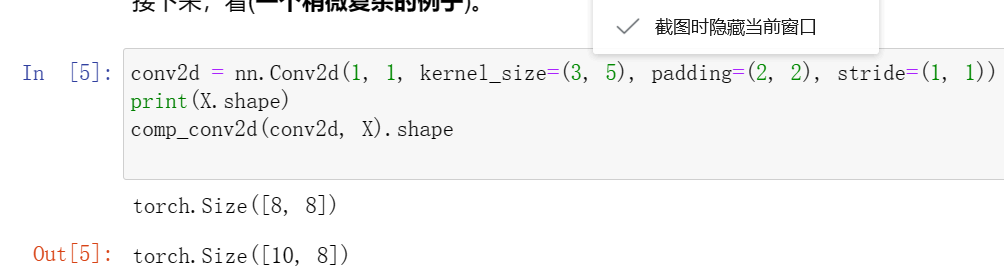
如何通过改变输入张量和卷积核张量，将互相关运算表示为矩阵乘法？
手工设计一些卷积核。
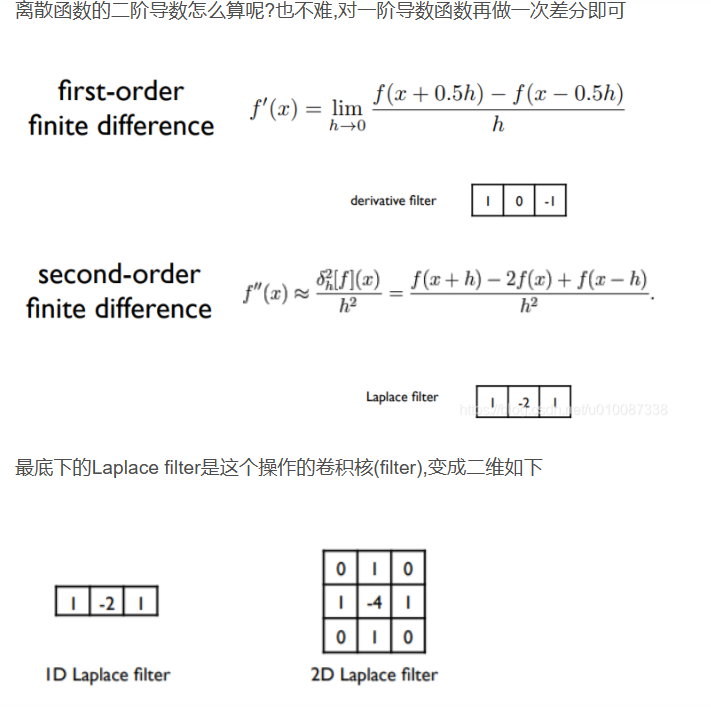
1. 二阶导数的核的形式是什么？
2. 积分的核的形式是什么？
3. 得到d次导数的最小核的大小是多少？

1.1结果如图

import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):  #@save
    """计算二维互相关运算"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

# 如果将本节中举例的卷积核K应用于X，会发生什么情况？
X = torch.eye(8)
K = torch.tensor([[1.0, -1.0]])
Y = corr2d(X, K)
print(Y)

tensor([[ 1.,  0.,  0.,  0.,  0.,  0.,  0.],
        [-1.,  1.,  0.,  0.,  0.,  0.,  0.],
        [ 0., -1.,  1.,  0.,  0.,  0.,  0.],
        [ 0.,  0., -1.,  1.,  0.,  0.,  0.],
        [ 0.,  0.,  0., -1.,  1.,  0.,  0.],
        [ 0.,  0.,  0.,  0., -1.,  1.,  0.],
        [ 0.,  0.,  0.,  0.,  0., -1.,  1.],
        [ 0.,  0.,  0.,  0.,  0.,  0., -1.]])

1.2 转置不影响结果

1.3 Y发生转置

tensor([[ 1., -1.,  0.,  0.,  0.,  0.,  0.,  0.],
        [ 0.,  1., -1.,  0.,  0.,  0.,  0.,  0.],
        [ 0.,  0.,  1., -1.,  0.,  0.,  0.,  0.],
        [ 0.,  0.,  0.,  1., -1.,  0.,  0.,  0.],
        [ 0.,  0.,  0.,  0.,  1., -1.,  0.,  0.],
        [ 0.,  0.,  0.,  0.,  0.,  1., -1.,  0.],
        [ 0.,  0.,  0.,  0.,  0.,  0.,  1., -1.]])

2 会报错

查看代码

 conv2d = Conv2D(kernel_size=(1, 2))

try:
  for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')
except Exception as e:
    print(e)

The size of tensor a (0) must match the size of tensor b (7) at non-singleton dimension 3

需要对输入进行调整

查看代码

 conv2d = Conv2D(kernel_size=(1, 2))

X = X.reshape((6, 8))
Y = Y.reshape((6, 7))
lr = 3e-2  # 学习率

try:
  for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')
except Exception as e:
    print(e)

查看代码

 import torch
from torch import nn
from d2l import torch as d2l

def conv2d_by_mul(X, K):
    # 获取卷积核大小
    h, w = K.shape
    # 计算输出图像大小
    outh = X.shape[0] - h + 1
    outw = X.shape[1] - w + 1
    # 调整卷积核形状以便做乘法
    K = K.reshape(-1, 1)
    # 将输入图像切成卷积核大小的块，打平成一维，存放在列表 Y 中
    Y = []
    for i in range(outh):
        for j in range(outw):
            Y.append(X[i:i + h, j:j + w].reshape(-1))
    # 将列表 Y 转为张量，每行代表一块的打平结果
    Y = torch.stack(Y, 0)
    # 用矩阵乘法表示互相关运算
    res = (torch.matmul(Y, K)).reshape(outh, outw)
    # 返回输出结果
    return res
X = torch.ones((2, 3))
X[:,1]=0
print(X)
K = torch.ones((2, 3))
conv2d_by_mul(X, K)

tensor([[1., 0., 1.],
        [1., 0., 1.]])

tensor([[4.]])

4这个没看懂题，看了看别人的博客还是有点晕

6.3. 填充和步幅

假设输入形状为 $n_{h} \times n_{w}$ ，卷积核形状为 $k_{h} \times k_{w}$ ，那么输出形状将是 $(n_{h} - k_{h} + 1) \times (n_{w} - k_{w} + 1)$ 。因此，卷积的输出形状取决于输入形状和卷积核的形状。

填充：为了防止丢失边缘像素。

步幅：在计算互相关时，卷积窗口从输入张量的左上角开始，向下、向右滑动。在前面的例子中，我们默认每次滑动一个元素。但是，有时候为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。

练习

1对于本节中的最后一个示例，计算其输出形状，以查看它是否与实验结果一致。

根据公式 outshape=⌊(nh−kh+ph∗2+sh)/sh⌋×⌊(nw−kw+pw∗2+sw)/sw⌋

输出应为： $[2.67, 2.25]$ ,向下取整，所以为 $[2, 2]。$

2在本节中的实验中，试一试其他填充和步幅组合。

3对于音频信号，步幅2说明什么？

对于音频信号而言，步幅为2就是以2为周期对信号进行采样计算。

4步幅大于1的计算优势是什么？

减小计算和内存压力，加快训练速度。

6.4. 多输入多输出通道

当多个通道存在时，需要对每个通道分别与卷积核运算，最后将各通道的结果求和。

在流行的神经网络架构中，通常也会增加输出通道的维数。

练习

1假设我们有两个卷积核，大小分别为 $k_{1}$ 和 $k_{2}$ （中间没有非线性激活函数）。

1.1证明运算可以用单次卷积来表示。

意思是，同时用两个卷积核做卷积运算吧。

1.2这个等效的单个卷积核的维数是多少呢？ K1*K2

1.3反之亦然吗？亦然

2假设输入为 $c_{i} \times h \times w$ 卷积核大小为 $c_{o} \times c_{i} \times k_{h} \times k_{w}$ ，填充为 $(p_{h}, p_{w})$ ，步幅为 $(s_{h}, s_{w})$ 。前向传播的计算成本（乘法和加法）是多少？

$f l o p s_{f or w a r d} = c_{i} \times c_{o} \times k_{h} \times k_{w} \times m_{h} \times m_{w}$

其中, m

3如果我们将输入通道 $c_{i}$ 和输出通道 $c_{o}$ 的数量加倍，计算数量会增加多少？如果我们把填充数量翻一番会怎么样？

根据t2等比增加

4如果卷积核的高度和宽度是 $k_{h} = k_{w} = 1$ ，前向传播的计算复杂度是多少？

co x $c_{i} \times h \times w$

5本节最后一个示例中的变量Y1和Y2是否完全相同？为什么？

理论上相同，但由于浮点运算的误差，可能会有微小差异。

6当卷积窗口不是 $1 \times 1$ 时，如何使用矩阵乘法实现卷积

可以将输入张量和卷积核张量分别展开为二维矩阵，然后对这两个矩阵进行乘法运算。

6.5. 汇聚层

汇聚（pooling）层，它具有双重目的：降低卷积层对位置的敏感性，同时降低对空间降采样表示的敏感性。

一般采用最大值或平均值来进行池化

练习

1尝试将平均汇聚层作为卷积层的特殊情况实现。

查看代码

 import torch.nn as nn 
import torch.nn.functional as F

class Net(nn.Module): 
    def init(self): 
      super(Net, self).init() 
      self.pool = nn.Conv2d(1, 1, 2) 
      # 平均池化层 
   
    def forward(self, x):
        x = F.avg_pool2d(x, (2, 2)) 
        # 平均池化层       
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]
        num_features = 1
        for s in size:
            num_features *= s
        return num_features
net = Net()
X = torch.arange(16, dtype=torch.float32).reshape((1,1,4, 4)) # 必须是1144，而44报错？ 因为必须设置通道数嘛
print(X)
Y=net(X)
print(Y)

tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])
tensor([[[[ 2.5000,  4.5000],
          [10.5000, 12.5000]]]])

2尝试将最大汇聚层作为卷积层的特殊情况实现。

将T1改为最大池化

3假设汇聚层的输入大小为 $c \times h \times w$ ，则汇聚窗口的形状为 $p_{h} \times p_{w}$ ，填充为 $(p_{h}, p_{w})$ 步幅为 $(s_{h}, s_{w})$ 。这个汇聚层的计算成本是多少？

flops=sh×swc×h×w×ph×pw

4为什么最大汇聚层和平均汇聚层的工作方式不同？

作用或者说目的不同，最大池化层通常用于提取输入张量中的显著特征，而平均池化层通常用于减少输入张量的大小并提高模型的计算效率。

5我们是否需要最小汇聚层？可以用已知函数替换它吗？

不需要吧，可以对负值做最大池化

查看代码

 import torch.nn.functional as F

def min_pool2d(x, kernel_size, stride=None, padding=0, dilation=1, ceil_mode=False): 
    neg_x = -x 
    neg_min_pool = F.max_pool2d(neg_x, kernel_size, stride=stride, padding=padding, dilation=dilation, ceil_mode=ceil_mode) 
    min_pool = -neg_min_pool 
    return min_pool
X = torch.arange(16, dtype=torch.float32).reshape((1, 1 ,4, 4))
print(X)
print(min_pool2d(X,2))

tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])
tensor([[[[ 0.,  2.],
          [ 8., 10.]]]])

6除了平均汇聚层和最大汇聚层，是否有其它函数可以考虑（提示：回想一下softmax）？为什么它不流行

其他函数，例如Lp池化和随机池化。softmax将输入转化我概率分布，将该函数用于池化可能会导致信息丢失。

6.6. 卷积神经网络（LeNet）

总体来看，LeNet（LeNet-5）由两个部分组成：

卷积编码器：由两个卷积层组成;
全连接层密集块：由三个全连接层组成。

卷积层->稠密块

为了将卷积块的输出传递给稠密块，我们必须在小批量中展平每个样本。换言之，我们将这个四维输入转换成全连接层所期望的二维输入。这里的二维表示的第一个维度索引小批量中的样本，第二个维度给出每个样本的平面向量表示。

练习

1将平均汇聚层替换为最大汇聚层，会发生什么？

平均汇聚层

2尝试构建一个基于LeNet的更复杂的网络，以提高其准确性。

2.1调整卷积窗口大小。2.2调整输出通道的数量。2.3调整激活函数（如ReLU）。2.4调整卷积层的数量。2.5调整全连接层的数量。2.6调整学习率和其他训练细节（例如，初始化和轮数）。

实验1

 net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

实验二增大卷积核和通道

net = nn.Sequential(
    nn.Conv2d(1, 8, kernel_size=7, padding=4), nn.Sigmoid(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(8, 16, kernel_size=7), nn.Sigmoid(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(256, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

改变激活函数（全改ReLU却精度极低）

net = nn.Sequential(
    nn.Conv2d(1, 8, kernel_size=7, padding=4), nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(8, 16, kernel_size=7),nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(256, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

调整卷积层数量

 net = nn.Sequential(
    nn.Conv2d(1, 8, kernel_size=7, padding=4), nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(8, 16, kernel_size=7),nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(16, 256, kernel_size = 4),nn.ReLU(),
    nn.Flatten(),
    nn.Linear(256, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

增加一层全连接

 net = nn.Sequential(
    nn.Conv2d(1, 8, kernel_size=7, padding=4), nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(8, 16, kernel_size=7),nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(16, 256, kernel_size = 4),nn.ReLU(),
    nn.Flatten(),
    nn.Linear(256, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 20),nn.Sigmoid(),
    nn.Linear(20, 10))

改变学习率和训练周期

 #lr, num_epochs = 0.9, 10
lr, num_epochs = 0.1, 40
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

3显示不同输入（例如毛衣和外套）时，LeNet第一层和第二层的激活值

输出第一层激活值

net = nn.Sequential(
    nn.Conv2d(1, 8, kernel_size=7, padding=4), nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(8, 16, kernel_size=7),nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(16, 256, kernel_size = 4),nn.ReLU(),
    nn.Flatten(),
    nn.Linear(256, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 20),nn.Sigmoid(),
    nn.Linear(20, 10))

输出函数

 #@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    x_first_Sigmoid_layer = net[0:2](X)[0:9, 1, :, :]
    d2l.show_images(x_first_Sigmoid_layer.reshape(-1, 30, 30).cpu().detach(), 1, 9)
    x_second_Sigmoid_layer = net[0:5](X)[0:9, 1, :, :]
    d2l.show_images(x_second_Sigmoid_layer.reshape(-1, 9, 9).cpu().detach(), 1, 9)
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

训练

 
lr, num_epochs = 0.1, 40
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

第一层是可以看到轮廓的，但第二层就很模糊。

posted @ 2023-07-16 21:09 浪矢-CL 阅读(164) 评论(0) 编辑收藏举报

刷新页面返回顶部

浪矢\n

AI-6卷积神经网络

6.3. 填充和步幅

6.4. 多输入多输出通道

6.5. 汇聚层

6.6. 卷积神经网络（LeNet）

公告