AI-2预备知识
2.1数据操作笔记
PyTorch和TensorFlow中的Tensor类型可做为张量使用，可支持GPU操作和自动微分。
广播机制：对不同形状的张量可使用广播机制进行运算。
为节省内存，可使用 X[:] = X + Y或X += Y来减少操作的内存开销。
2.1练习
1运行本节中的代码。将本节中的条件语句X==Y更改为 X < Y 或 X > Y，然后看看你可以得到什么样的张量。
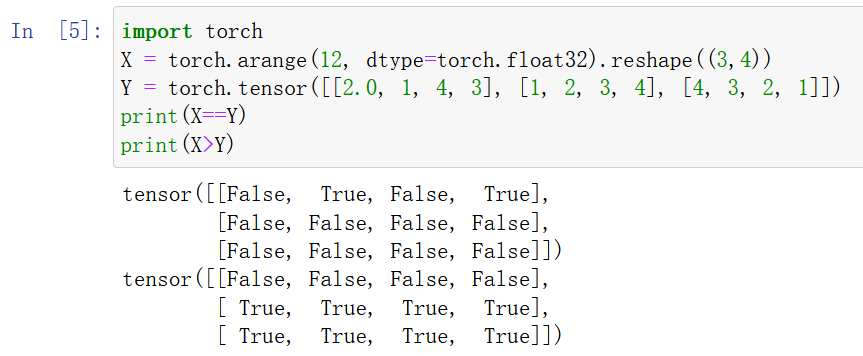
2用其他形状（例如三维张量）替换广播机制中按元素操作的两个张量。结果是否与预期相同？
同样会使用广播机制
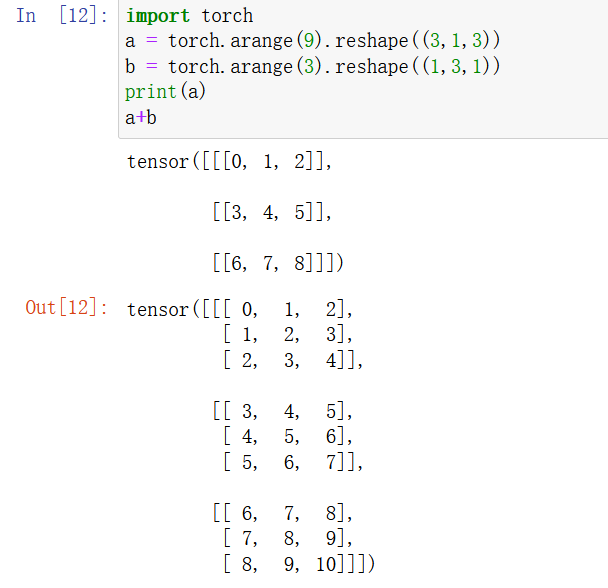
2.2数据预处理
csv类型文件,使用os包的读写操作。
pandas包的read_csv函数似乎也比较常用，可直接读入整个表格。
对于缺失值的处理，有两种方法，一是插值法：插入省缺值NaN , 二是删除法
2.2练习
创建包含更多行和列的原始数据集。
1删除缺失值最多的列。
def drop_max(m):
num = m.isna().sum() #获得缺失值统计信息
num_dict = num.to_dict() #转为字典
max_col =max(num_dict,key=num_dict.get) #取字典中最大值的键
del m[max_col] #删除缺失值最多的列
return m2将预处理后的数据集转换为张量格式。
2.3线性代数
在python中，张量与标量的运算不会改变张量的形状，而是会将标量与张量的每一个元素都进行运算。
张量之间的运算：向量点积，矩阵-向量积，矩阵乘法
书中特别强调了矩阵乘法和Hadamard积的区别(暂时未见过Hadamard积的应用)
2.3练习
1证明一个矩阵A的转置的转置是A，即(A⊤)⊤=A。
2给出两个矩阵A和B，证明“它们转置的和”等于“它们和的转置”，即A⊤+B⊤=(A+B)⊤。
3给定任意方阵A，A+A⊤总是对称的吗?为什么?
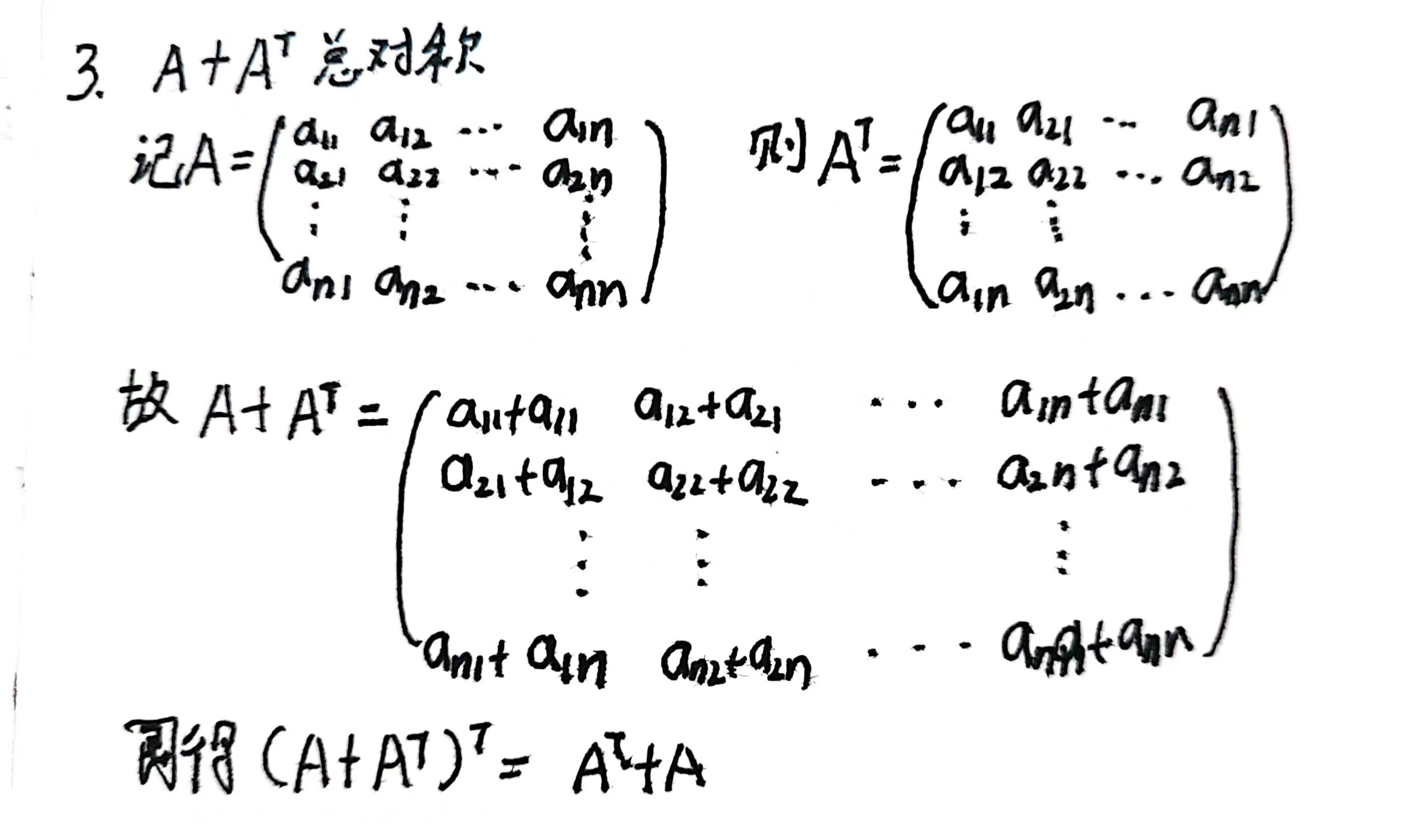
4本节中定义了形状(2,3,4)的张量X。len(X)的输出结果是什么？
5对于任意形状的张量X,len(X)是否总是对应于X特定轴的长度?这个轴是什么?
是，为第一维度的轴
6运行A/A.sum(axis=1)，看看会发生什么。请分析一下原因
参数为0可以运行，参数为1则无法运算。原因是矩阵除向量，长度需要对齐。
7考虑一个具有形状(2,3,4)的张量，在轴0、1、2上的求和输出是什么形状?
8 为linalg.norm函数提供3个或更多轴的张量，并观察其输出。对于任意形状的张量这个函数计算得到什么?
结果显示，范数结果与形状无关
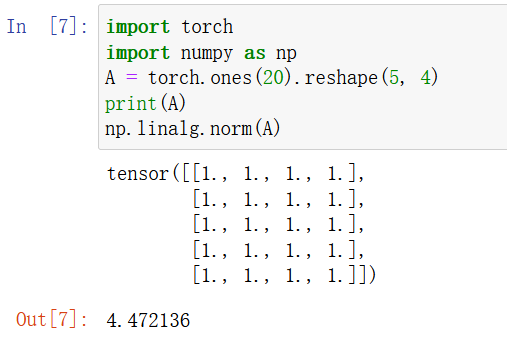
2.4微积分
在深度学习中梯度的计算是一个很重要的环节，通过链式法则可以求复合函数的梯度。
1绘制函数y=f(x)=x**3−1/x和其在x=1处切线的图像。
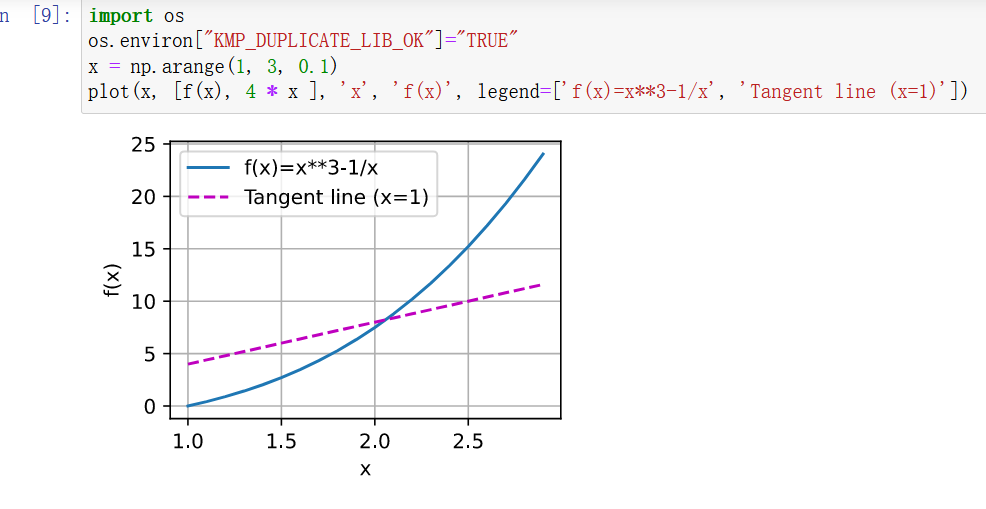
2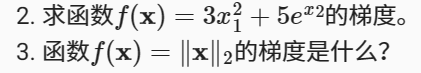
解
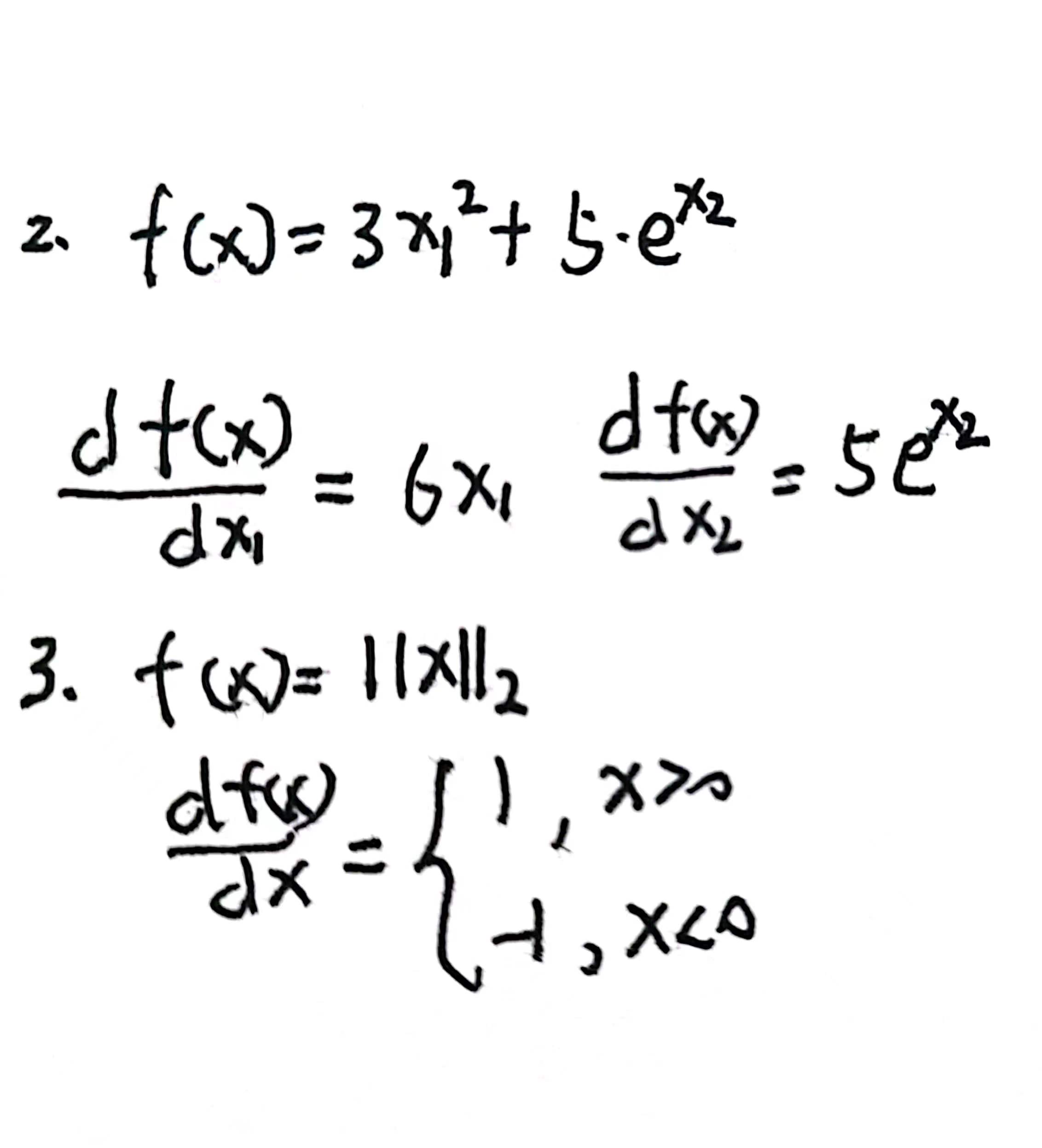
4尝试写出函数u=f(x,y,z)，其中x=x(a,b)，y=y(a,b)，z=z(a,b)的链式法则。
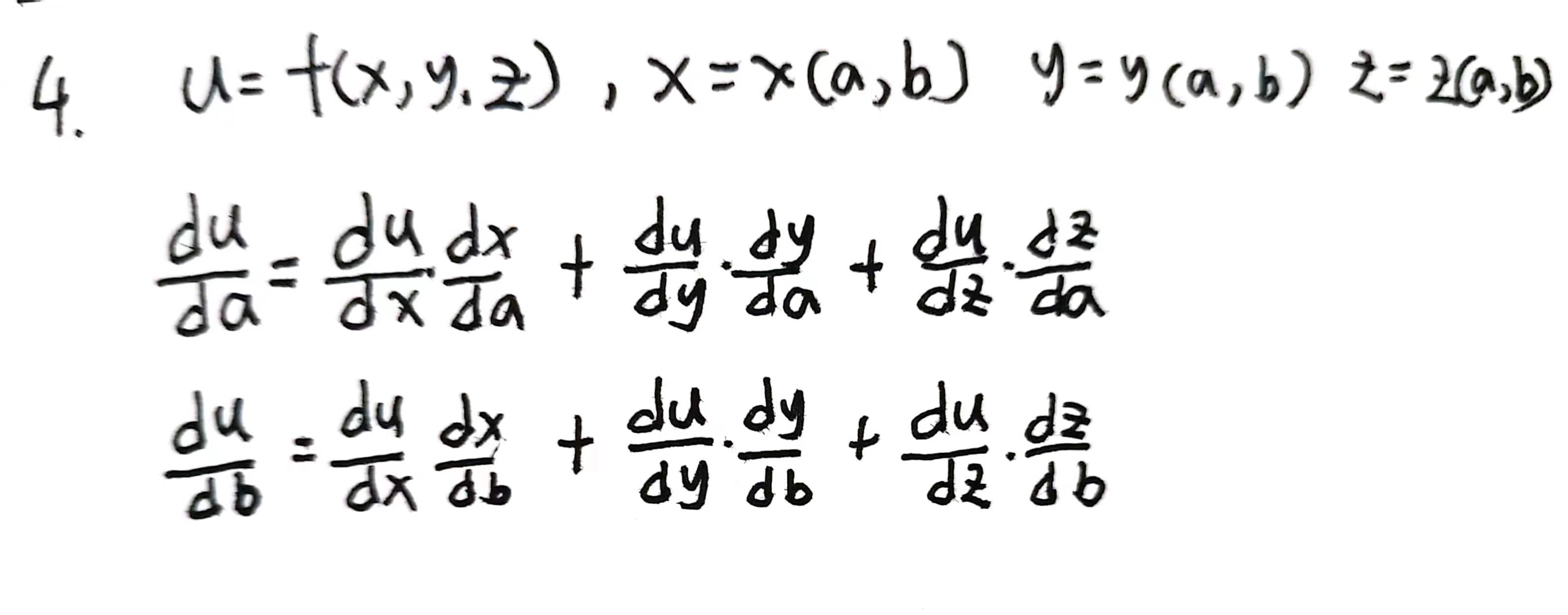
2.5自动微分
通过深度学习框架自动求导，通过自动微分反向传播。
简单的样例是：
y.backward()
x.grad这样即可得到y关于x的导数。
一个很特殊的地方，分离计算时将某一部分视为
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u自动微分还有一个好处是，对于含有条件分支和循环语句这样的函数，也可以得到变量的梯度。
2.5练习
1为什么计算二阶导数比一阶导数的开销要更大？
因为二阶导是在一阶导数的基础上再次进行求导。
2在运行反向传播函数之后，立即再次运行它，看看会发生什么。
pytoch构建的计算图是动态图，为了节约内存，所以每次一轮迭代完也即是进行了一次backward函数计算之后计算图就被在内存释放。因此反向传播后，再次运行反向传播会报错。
参考自 https://blog.csdn.net/sinat_28731575/article/details/90342082
3在控制流的例子中，我们计算d关于a的导数，如果将变量a更改为随机向量或矩阵，会发生什么？
4重新设计一个求控制流梯度的例子，运行并分析结果。
5使f(x)=sin(x)，绘制f(x)和 df(x) / dx 的图像，其中后者不使用f′(x)=cos(x)。
2.6概率
机器学习就是根据已有数据对未来样本做出预测。本节简略描述的概率的一些概念。
2.6练习
1进行m=500组实验，每组抽取n=10个样本。改变m和n，观察和分析实验结果。
2给定两个概率为p(A)和p(B)的事件，计算p(A∪B)和p(A∩B)的上限和下限。（提示：使用友元图来展示这些情况。)
3假设我们有一系列随机变量，例如A、B和C，其中B只依赖于A，而C只依赖于B，能简化联合概率p(A,B,C)吗？（提示：这是一个马尔可夫链。)
4在 2.6.2.6节中，第一个测试更准确。为什么不运行第一个测试两次，而是同时运行第一个和第二个测试?
