[CJ NOIP模拟赛] 细胞（cell）
1. 题目大意
第 \(i\) 天向容器放入 \(i\) 个细胞，每个细胞每过一天可以分裂出（注意不是分裂成） \(x-1\) 个细胞，求第 \(n\) 天细胞个数 \(\% w\) 的值。
对于 \(30\%\) 的数据，\(n \le 10^7\)，暴力即可。
对于所有数据，\(n \le 2^{63} - 1\) 且 \(1 \le x, w \le 2^{31} - 1\)，矩阵快速幂。
另外地，\(10\%\) 的数据保证 \(x = 1\)，即细胞不会分裂，答案使用等差数列求和即可。
2. 前言
膜你退火，膜我退役
这道傻逼题我推了好久，算半天脑子一热以为是秦九韶公式。又算好久，搞出来个复杂的分数套分数，最终这些算法复杂度也还是 \(O(n)\) ，而且这些乱七八糟的公式算法比递推还复杂，差点砸电脑。
最后还是想到了矩阵快速幂。量级贼大、数值贼高、有固定的递推公式的，如斐波那契数列，十有八九可以使用矩阵快速幂。 矩阵快速幂使用很广泛，常用于优化；还有我们熟知的 高斯消元，就要用到矩阵。
具体矩阵是什么、怎么操作、有什么性质，御·Dragon后期将会有详解，敬请期待。
3. 正题
3.1 部分分
应对不同的部分分做法，在“题目大意”中已经大概介绍，这里就放个暴力的代码算了吧。
值得注意的是，这里需要开 \(long long\)，且取模时精度、溢出需要维护一下。
if(x == 1)
{
if(n & 1)
printf("%lld\n",((((n+1)>>1)%w)*(n%w))%w);
else
printf("%lld\n",(((n>>1)%w)*((n+1)%w))%w);
return 0;
}
for(rg ll i = 1; i <= n; ++i)
ans = (((ans*x)%w) + i) % w;
printf("%lld\n", ans%w);
3.2 正解
矩阵快速幂
不妨设第 \(i\) 天的细胞个数为 \(F_i\)，由题意得，\(F_i = F_{i-1} + (x-1) \times F_{i-1} + i\)，化简得 \(F_i = x \times F_{i-1} + i\)。
我们希望能 构造一个初始矩阵，找到（推出）转移矩阵，最后答案矩阵即 \(S\) = 初始矩阵 \(\times\) \(转移矩阵^n\)，答案就藏在 \(S\) 的某个位置中（具体藏在哪里，要看你设的初始矩阵定义）。
============================================================================
我们设第 \(i\) 天的矩阵为 \([原有细胞数\ \ \ 新增细胞数\ \ \ i的递增常数]\)
故，我们得到初始矩阵：
\begin{equation}
F_1 = {
\left[ \begin{array}{ccc}
0 & 1 & 1
\end{array}
\right ]}
\end{equation}
经过\(*#@!#￥%……&*\)操作和\(*&^%(*&!#@\)定理可以得到转移矩阵 \(T\) ：
============================================================================
我们来手动模拟一下。已知
\begin{equation}
F_1 = {
\left[ \begin{array}{ccc}
0 & 1 & 1
\end{array}
\right ]}
\end{equation}
让 \(F_1\) 矩阵 \(\times\) 转移矩阵\(T\) 即可得到 \(F_2\)
而 \(F_2\) 矩阵正好印证了我们对于矩阵的设定 \([原有细胞数\ \ \ 新增细胞数\ \ \ i的递增常数]\)
以此类推（\(LaTex\) 太 \(TM\) 难写了）
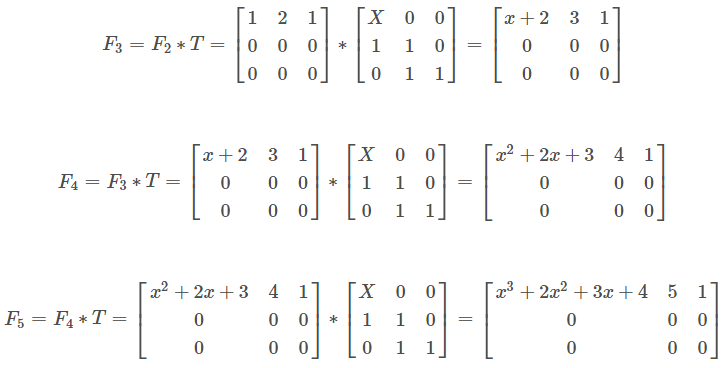
最终得到
附上答案的公式 \(F_n = x^{n-2} + 2\ x^{n-3} + 3\ x^{n-4} ······ + (n-1)\ x + (n-2)\)
3. 代码
#include<bits/stdc++.h>
#include<cctype>
#pragma GCC optimize(2)
#define in(u) u = read()
#define out(a) write(a),putchar(' ')
#define outn(a) out(a),putchar('\n')
#define ll long long
#define rg register
#define New ll
using namespace std;
namespace IO_Optimization{
inline New read()
{
New X = 0,w = 0;
char ch = 0;
while(!isdigit(ch))
{
w |= ch == '-';
ch=getchar();
}
while(isdigit(ch))
{
X = (X << 3) + (X << 1) + (ch ^ 48);
ch = getchar();
}
return w ? -X : X;
}
inline void write(New x)
{
if(x < 0) putchar('-'),x = -x;
if(x > 9) write(x/10);
putchar(x % 10 + '0');
}
#undef New
}
using namespace IO_Optimization;
const int MAXN = 10 + 2;
ll n, mod;
struct Matrix
{
ll m[MAXN][MAXN]; //矩阵数组m
Matrix()
{
memset(m, 0, sizeof(m));
}
};
inline Matrix multiply(Matrix x, Matrix y) //定义矩阵相乘的函数
{
Matrix res; //存结果的矩阵
for(rg int k = 1;k <= 3; ++k)
for(rg int i = 1;i <= 3; ++i)
for(rg int j = 1;j <= 3; ++j)
res.m[i][j] = (res.m[i][j] + x.m[i][k] * y.m[k][j] % mod) % mod;
return res;
}
int main()
{
freopen("cell.in","r",stdin);
freopen("cell.out","w",stdout);
Matrix a, b;
int x;
in(n), in(x), in(mod);
a.m[1][1] = x, a.m[2][1] = a.m[2][2] = a.m[3][2] = a.m[3][3] = 1; //快速幂的矩阵
b.m[1][1] = 0, b.m[1][2] = b.m[1][3] = 1; //我们构造的初始矩阵
while(n)//快速幂
{
if(n & 1)
b = multiply(b, a);
a = multiply(a, a);
n >>= 1;
}
out(b.m[1][1]);//输出即可
return 0;
}
