洛谷P4017 最大食物链计数 题解
\(2020\) 年 \(3\) 月 \(17\) 日更博报告:
1 月的更新虽然完善了一些问题,但是讲得比较快,有些同学看不大懂,故再次更新,还有什么不懂的请私信我。
由于阿里云的各种问题,使得原本在博客园中排版精美的源码在这里丑陋不堪。故更好的阅读效果请点击这里
\(2020\) 年 \(9\) 月 \(5\) 日更博报告:
士别三日,刮目相待。更新一些细节的描述,优化排版。希望这篇题解能够帮助更多初学者,成为最好的题解。
文字讲解
题目分析:
首先 ,要知道这道题是 \(Topo\) 拓扑排序。不妨先从拓扑排序定义下手,分析题目的性质。经分析得:
食物链中的生物 —— 节点
生物之间的关系 —— 有向边
为了方便描述,我们将
不会捕食其他生物的 生产者 叫做 最佳生产者
不会被其他生物捕食的 消费者 叫做 最佳消费者
由于数据中不会出现环,所以 最大食物链 即 左端是 最佳生产者 ,右端是 最佳消费者 的路径
而 只要最左端是 最佳生产者 的路径(即最右端可以不是 最佳消费者 的最大食物链) 我们称之为 类食物链
既然 食物链中的生物 可以看成 节点,那么 最佳生产者 的入度一定为 \(0\), 而 最佳消费者 的出度也为 \(0\)
思路引导
想要找到一条 最大食物链 ,那么这条路径的 起点 入度要为0,终点 出度要为0。 故:
既要记录入度,还要记录出度!
现在的问题转换成了,如何找到图中所有 左端点入度为0 且 右端点出度为0 的路径的数量
正解
我们拿起笔,在草稿纸上画一个图进行推算。接下来将使用 样例 进行举例。
(将 最佳生产者 涂上 蓝色,最佳消费者 涂上 红色)
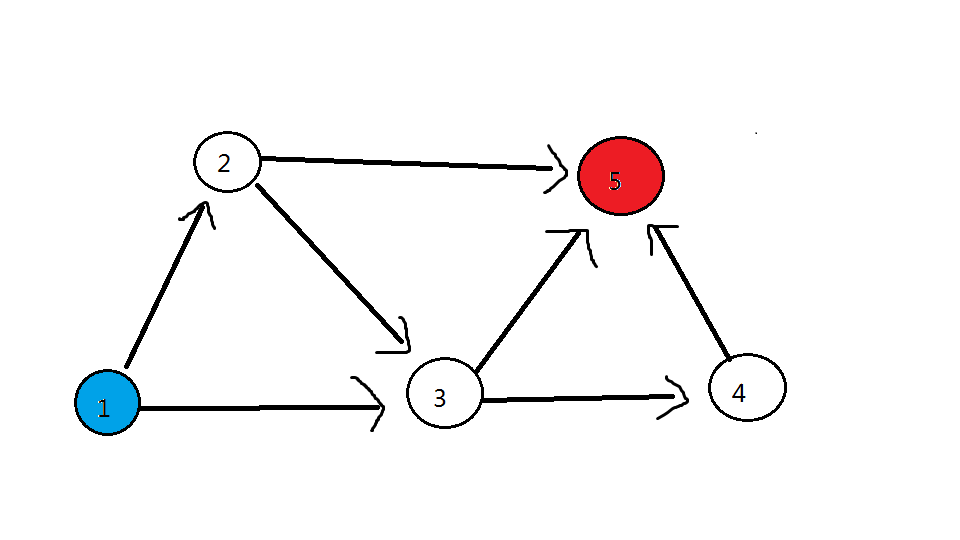
发现: 答案为 到所有 红色点 的路径条数的 总和
(这里的 路径条数总和 不是 连向它有几条边 ,而是以它结束的 最大食物链 数量的总和)
对于上图,\(5\) 号点的对应路径数量 取决于:以 到 \(5\) 号点的三个点( \(2\) 号、\(3\) 号、\(4\) 号) 结尾的 类食物链 条数的总和。
而 以 \(2\) 号、\(3\) 号、\(4\) 号 结尾的 类食物链 取决于:以 可以到达 \(2\) 号、\(3\)号、\(4\)号点 的点 结尾的 类食物链 条数的总和。
以此类推,显然对于 以 任一点 结尾的 类食物链 的数量,都取决于 蓝色点
各点数量对应关系在下图用绿色边标注
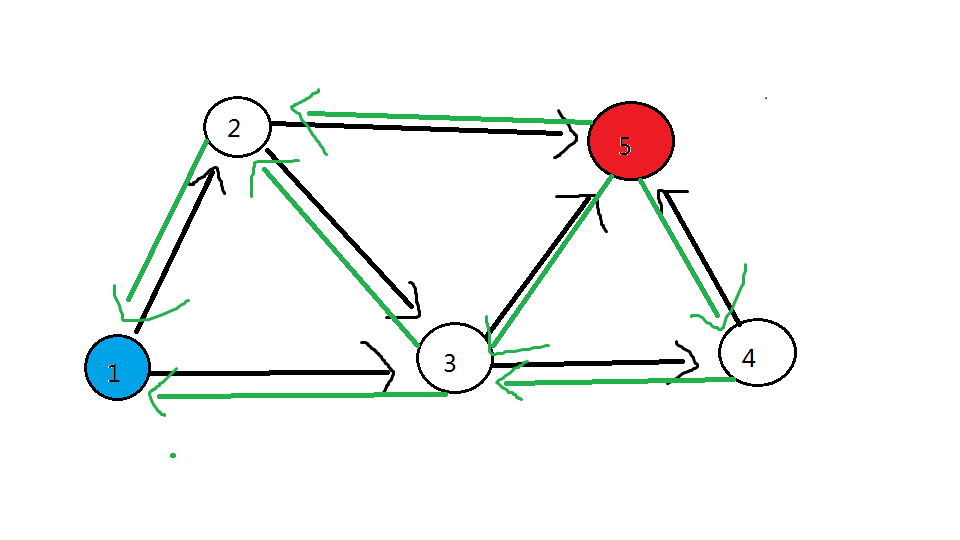
重点:
使用拓扑排序,由题意得知 \(Topo\) 排序第一轮被删掉的点 一定是 蓝色点(最佳生产者),而令 蓝色点 的答案为 \(1\)。
当第一轮删点时,将蓝色点可以到的点 的答案 都加上 蓝色点的 答案(即加 \(1\))。
即:拓扑排序 需要删除的点的答案 都累加到 它可以到达的点 上面去
这样我们就将边的累加 转换到了 点之间的累加。
最后累加所有 红色点(最佳消费者) 的答案,输出即可。
以第 i 号点结束的 类食物链 数量 = 以 可到达 i 号点 的点 结尾的 类食物链 数量的和
以下是模拟操作过程:
加载时间较慢,请稍等
第一轮:删除 \(1\) 号蓝色点,\(1\) 号蓝色点可以到的点(\(2\) 号点、\(3\) 号点)都加 \(1\)
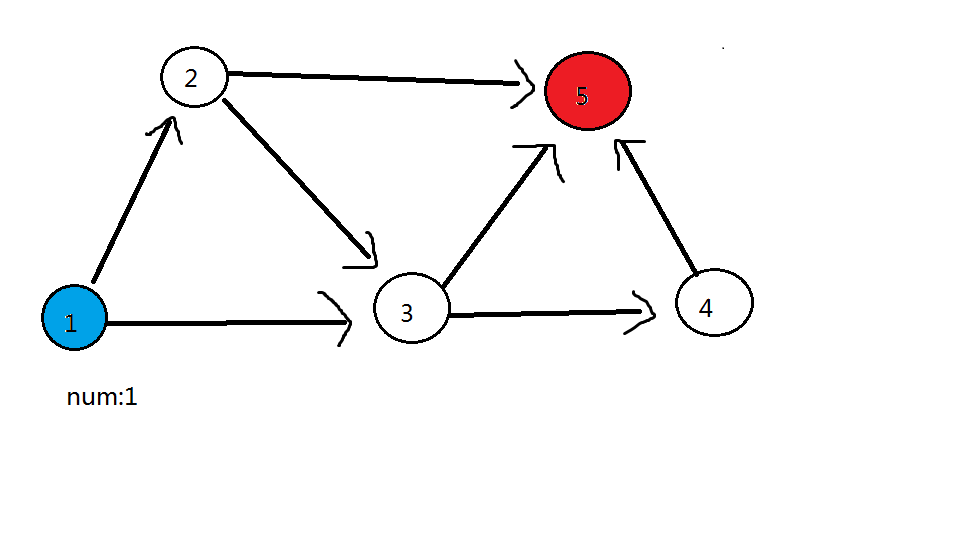
第二轮:删除 \(2\) 号点,\(2\) 号点可以到的点(\(3\) 号点、\(5\) 号红色点)都加 \(1\)。此时 \(3\) 号点答案为 \(2\),\(5\) 号点答案为 \(1\)
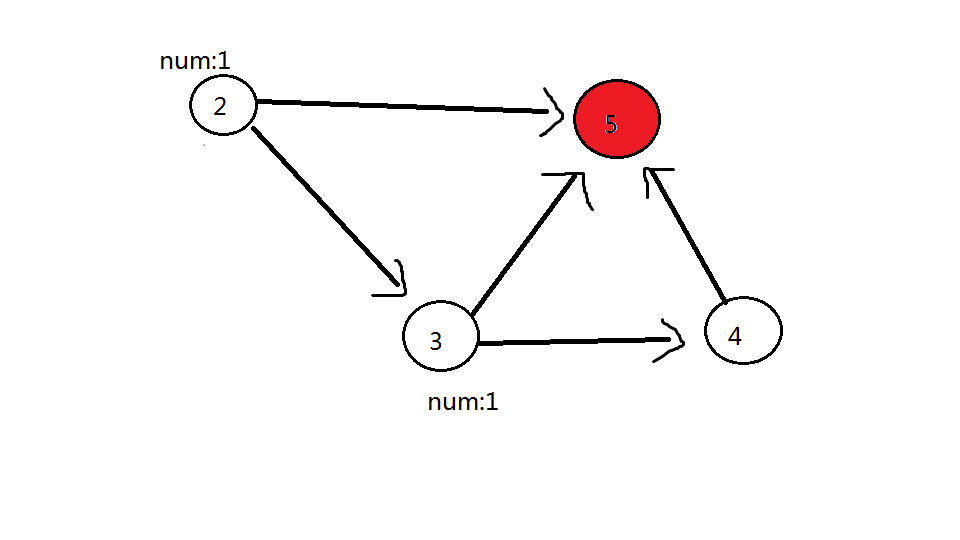
第三轮:删除 \(3\) 号点,\(3\) 号点可以到的点(\(4\) 号点、\(5\) 号红色点)都加 \(2\)。此时 \(5\) 号点答案为 \(3\),\(4\) 号点答案为 \(2\)
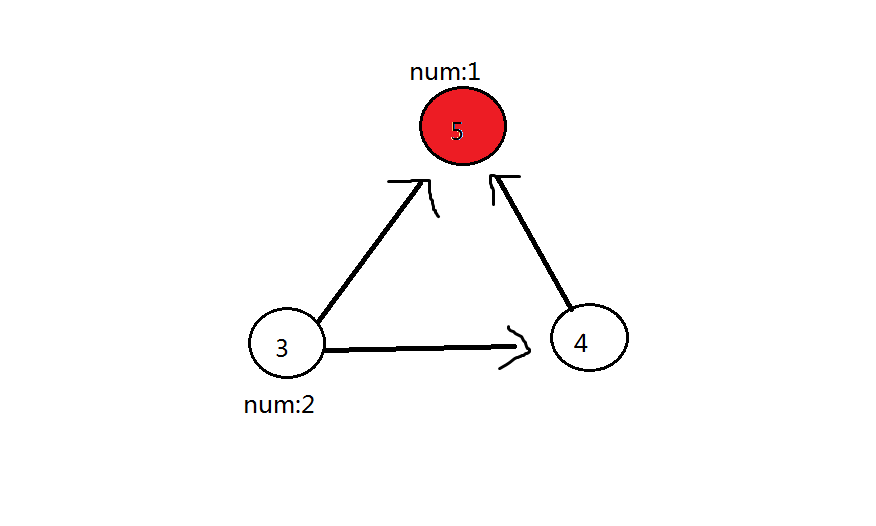
第四轮:最后删除 \(4\) 号点,\(4\) 号点可以到的点(\(5\) 号红色点)加 \(2\),此时 \(5\) 号点答案为 \(5\)
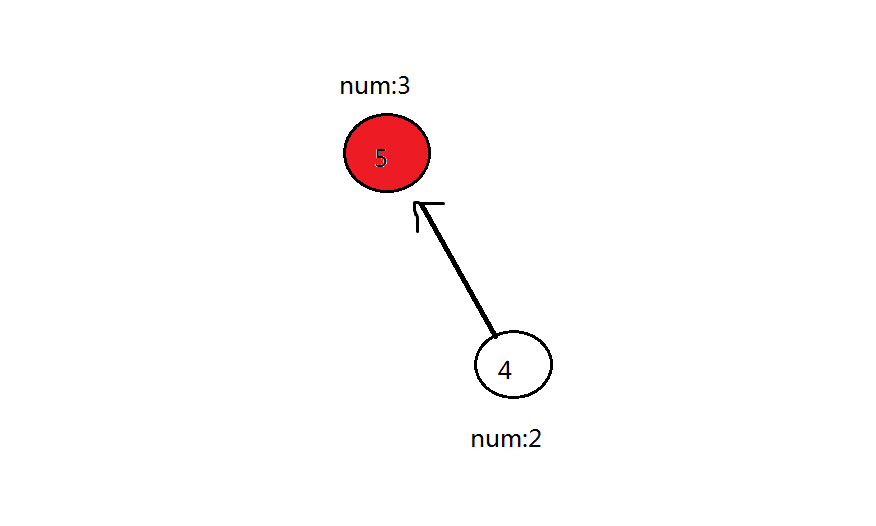
可见全图只有 \(5\) 号一个红色点,那么答案就是 \(5\) 号点的答案—— \(5\) 了
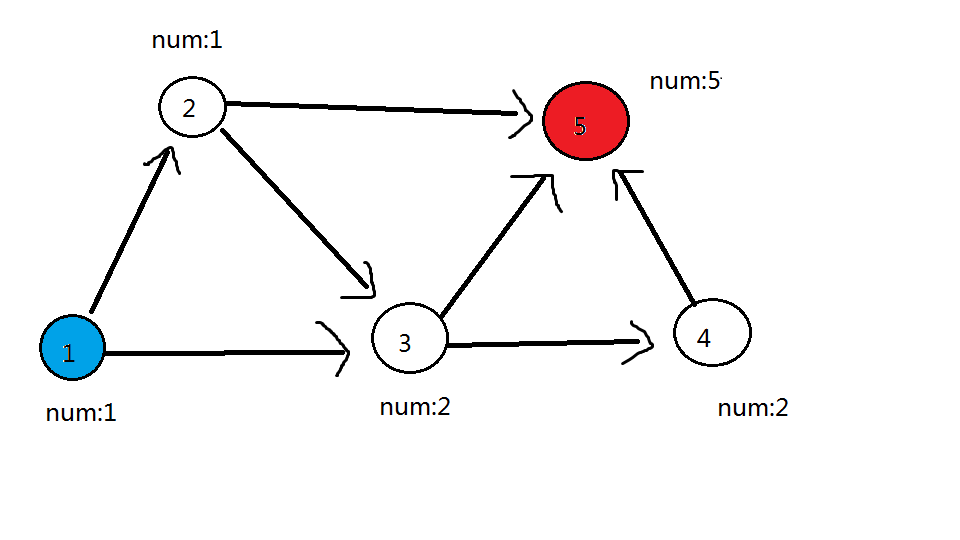
那么代码实现就很简单了!
上代码:
#include<bits/stdc++.h>
#include<cctype>
#pragma GCC optimize(2)
#define ll long long
#define rg register
#define New int
//上面这些花里胡哨的东西请忽略
using namespace std;
inline New read()//快速读入
{
New X = 0,w = 0;
char ch = 0;
while(!isdigit(ch))
{
w |= ch == '-';
ch=getchar();
}
while(isdigit(ch))
{
X = (X << 3) + (X << 1) + (ch ^ 48);
ch = getchar();
}
return w ? -X : X;
}
char F[200] ;
inline void write(New x) //快速输出
{
if(x == 0)
{
putchar('0');
return;
}
New tmp = x > 0 ? x : -x;
int cnt = 0;
if(x < 0)
putchar( '-' );
while(tmp > 0)
{
F[cnt++] = tmp % 10 + '0';
tmp /= 10;
}
while(cnt > 0)
putchar(F[--cnt]) ;
}
const int N = 5e3 + 2; //定义常量大小
const int mod = 80112002; //定义最终答案mod的值
int n, m; //n个点 m条边
int in[N], out[N]; //每个点的入度和出度
vector<int>nei[N]; //存图,即每个点相邻的点
queue<int>q; //拓扑排序模板所需队列
int ans; //答案
int num[N]; //记录到这个点的类食物连的数量,可参考图
signed main()
{
n = read(), m = read();
for(rg int i = 1; i <= m; ++i)
{ //输入边
int x = read(), y = read();
++in[y], ++out[x]; //右节点入度+1,左节点出度+1
nei[x].push_back(y); //建立一条单向边
}
for(rg int i = 1; i <= n; ++i) //初次寻找入度为0的点(最佳生产者)
if(!in[i])
{ //是最佳生产者
num[i] = 1; //初始化
q.push(i); //压入队列
}
while(!q.empty())
{ //只要还可以继续Topo排序
int tot = q.front();//取出队首
q.pop();//弹出
int len = nei[tot].size();
for(rg int i = 0;i < len; ++i)
{ //枚举这个点相邻的所有点
int next = nei[tot][i]; //取出目前枚举到的点
--in[next];//将这个点的入度-1(因为目前要删除第tot个点)
num[next] = (num[next] + num[tot]) % mod;//更新到下一个点的路径数量
if(in[next] == 0)q.push(nei[tot][i]);//如果这个点的入度为0了,那么压入队列
}
}
for(rg int i = 1; i <= n; ++i) //寻找出度为0的点(最佳消费者)
if(!out[i]) //符合要求
ans = (ans + num[i]) % mod;//累加答案
write(ans);//输出
return 0;//end
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号