Fisher线性判别分析
Fisher线性判别分析
1、概述
在使用统计方法处理模式识别问题时,往往是在低维空间展开研究,然而实际中数据往往是高维的,基于统计的方法往往很难求解,因此降维成了解决问题的突破口。
假设数据存在于d维空间中,在数学上,通过投影使数据映射到一条直线上,即维度从d维变为1维,这是容易实现的,但是即使数据在d维空间按集群形式紧凑分布,在某些1维空间上也会难以区分,为了使得数据在1维空间也变得容易区分,需要找到适当的直线方向,使数据映射在该直线上,各类样本集群交互较少。如何找到这条直线,或者说如何找到该直线方向,这是Fisher线性判别需要解决的问题。
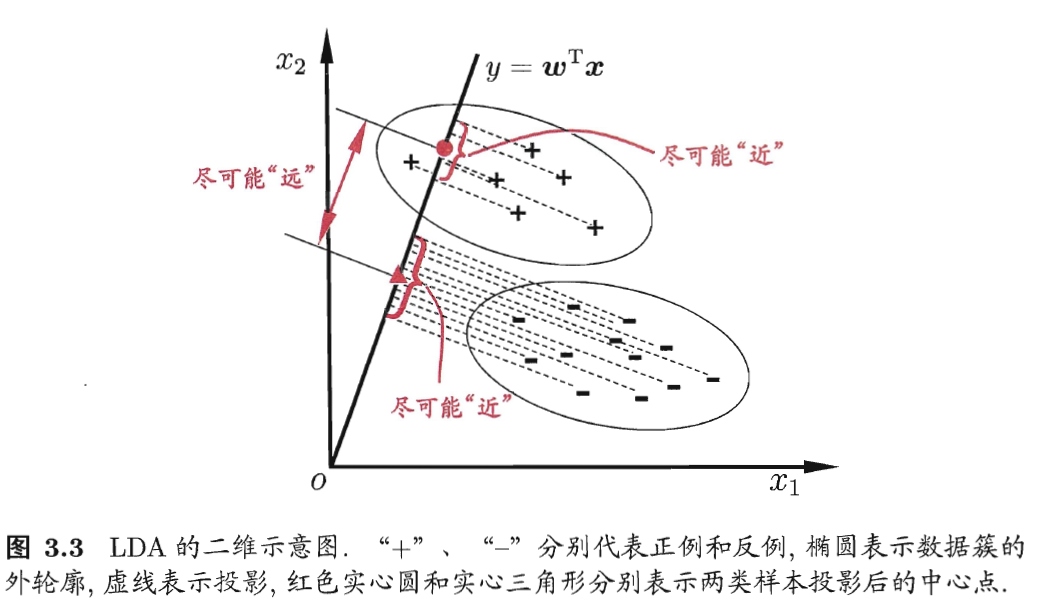
2、从d维空间变换到1维空间

3、介绍几个基本的参量
A. 在d维原始空间

B. 在1维映射空间

4、Fisher准则函数

5、学习算法推导




6、决策分类






