二分与三分与二分快速幂
二分是一种常用而且非常精妙的算法,常常是我们解决问题的突破口。二分的基本用途是在单调序列或单调函数中做查找操作。因此,当问题的答案具有单调性时,就可以通过二分把求解转化为判定(根据复杂度理论,判定的难度小于求解)。进一步的,我们还可以通过三分(适用于求解凸性函数)解决单峰函数的极值以及相关问题。
- 二分
思想:分而治之。将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立且与原问题相同,(如果子问题的规模仍然不够小,,再划分为k个子问题),然后递归的求解这些子问题,最后用适当的方法将各个子问题的解合并成原问题的解。
方法:a)二分查找:在一个单调有序的集合或函数中查找一个解,每次分为左右两部分,判断解在哪个区间(并调节上下界),并直到找到目标元素。
int binary_search(int x) {
int l = 0, r = n;
while (l < r) {
int mid = (l + r) >> 1;
if (a[mid] == x) {
return mid;
}
if (a[mid] < x) {
l = mid + 1;
} else {
r = mid;
}
}
return - 1;
}
b)二分答案:(最大值最小或最小值最大这类问题)这类双最值问题常常选用二分法求解(二分之后,先假装自己确定答案),配合贪心,DP等算法,检验这个答案是否合理,将最优化问题转化为判定性问题。
c)代替三分:(对于单峰函数)二分导函数求函数极值。
例题:Bzoj1734 Poj2018 ... ...
借书(2018沈阳集训Day4 - 二分答案)
题目描述
输入
5
7
1
17
13
10
输出
如果Dilhao给出其他任何三本书,其中的两本书难度差的最小值都小于7,所以ldxxx出题的最大复杂程度为7。
数据说明
对于 30%的数据: 2<=n<=20;
对于 60%的数据: 2<=n<=1000;
对于 100%的数据: 2<=n<=100000, 2<=m<=n, 0<=ai<=1000000000。
// 二分答案
#include <iostream> #include <algorithm> using namespace std; long long diff[100010]; long long n, m, tmp, num_book; bool check (long long x) { num_book = 1; long long tmp = diff[1]; long long flag_one = 1; while (num_book < m) { long long next = tmp + x; long long flag = lower_bound(diff + flag_one, diff + n + 2, next) - diff; if (flag == n + 1) { return false; } num_book += 1; flag_one = flag; tmp = diff[flag]; } return true; } int main() { freopen("margin.in", "r", stdin); freopen("margin.out", "w", stdout); cin >> n >> m; for (int i = 1; i <= n; i++) { cin >> diff[i]; } sort(diff + 1, diff + n + 1); long long l = 0; long long r = diff[n]; long long ans; diff[n + 1] = 2 * diff[n]; while (l <= r) { long long mid = (l + r) / 2; if (check(mid) == true) { ans = mid; l = mid + 1; } else if (check(mid) == false) { r = mid - 1; } } cout << ans << endl; return 0; }
- 三分
适用于凸性函数的极值问题(二次函数就是一个典型的单峰函数)。与二分法强调函数的单调性不同,三分法强调函数的单峰性。
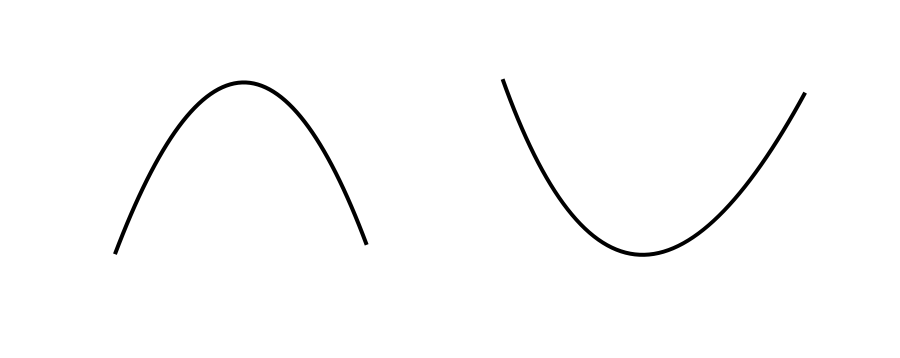
在区间 [L,R] [L,R] 中找两个三分点,也就是 mid 和 mmid,然后比较这两个点的 y 值大小。如果是计算最大值的情况,那么 y (mid) ≤ y (mmid),说明最大值肯定在 mid 右边,这时把区间变成 [mid , R],反之变成 [L , mmid] ,直到 LL 和 RR 很接近为止。如果是求最小值的情况就反过来。
double cal() {
double l = 0, r = pi / 2;
while (r - l > eps) {
double mid = (l + r) / 2;
double mmid = (mid + r) / 2;
if (f(mid) < f(mmid)) {
l = mid;
}
else {
r = mmid;
}
}
return l;
}
- 二分快速幂
c/c++ 的 <math> 库中有 pow 函数(pow(double a, double b)),但一般都是用来计算浮点数的,函数的时间复杂度是 O(b) 。有些时候,a,b 都是整数,且 b 比较大(1e8),我们肯定需要一些优化方法,那就是快速幂。
快速幂有很多种写法,但是结合二分的思想,无疑比递归要快很多。
(递归写法)
// 递归
int pw1(int x, int y, int p) { if (!y) { return 1; } int res = pw1(x, y / 2, p); res = res * res % p; if (y & 1) { res = res * x % p; } return res; }
(二分写法)
// 二分
int pw2(int x, int y, int p) { int res = 1; while (y) { if (y & 1) { res = res * x % p; } y >>= 1; x = x * x % p; } return res; }



