实验三 查找与排序
实验三 查找与排序
实验1
题目
完成教材P302 Searching.Java ,P305 Sorting.java中方法的测试
不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位
提交运行结果图(可多张)
代码与问题
对于这个实验来说我们在之前的课上就已经完成了基本上所有的代码,就只是添加了一部分的测试用例,所以就没有在代码方面遇到太多的问题,对于测试来说也是比较的顺利。
截图
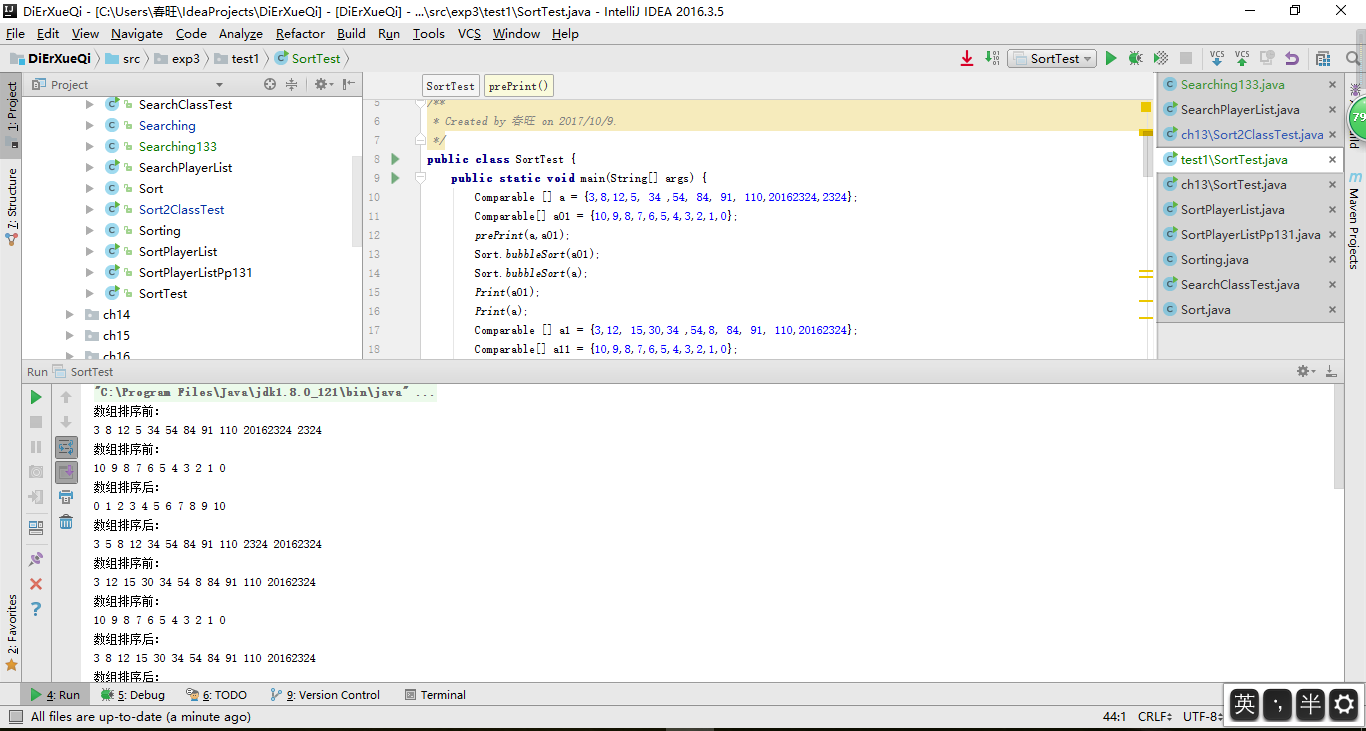
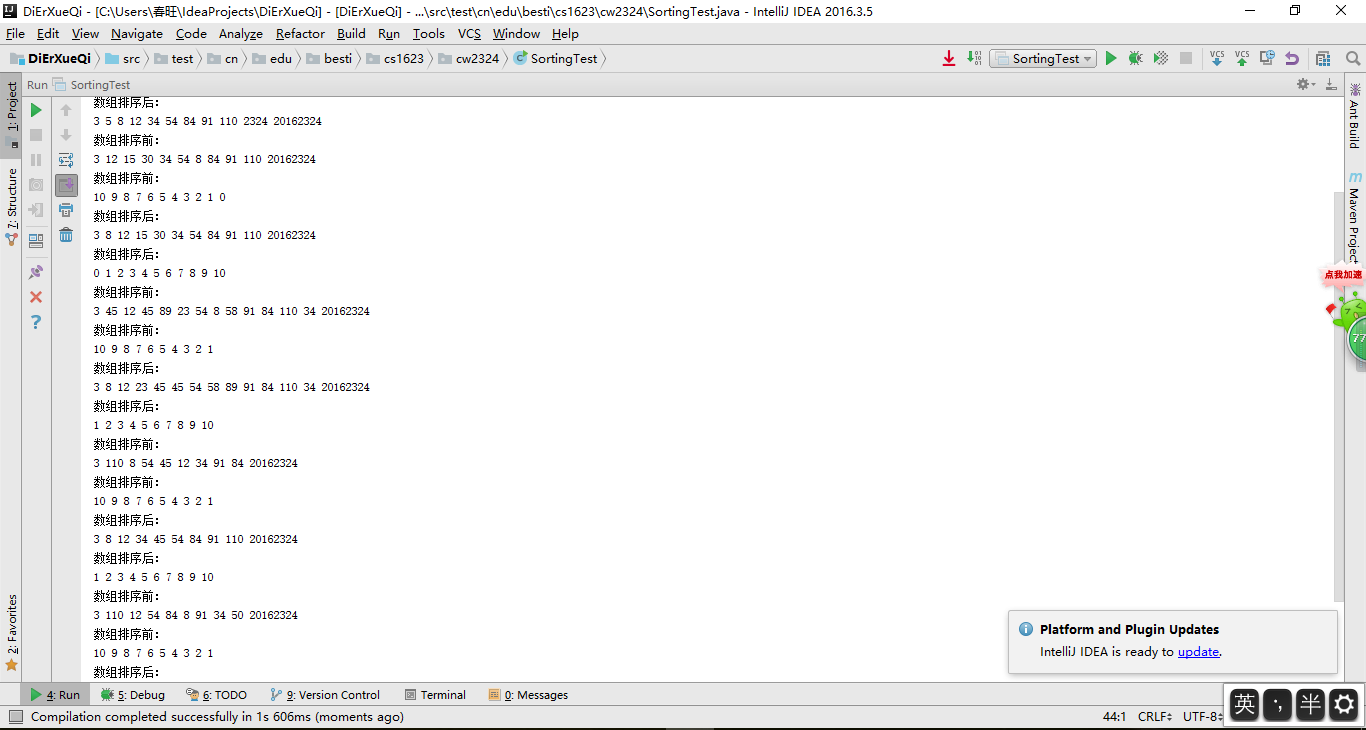
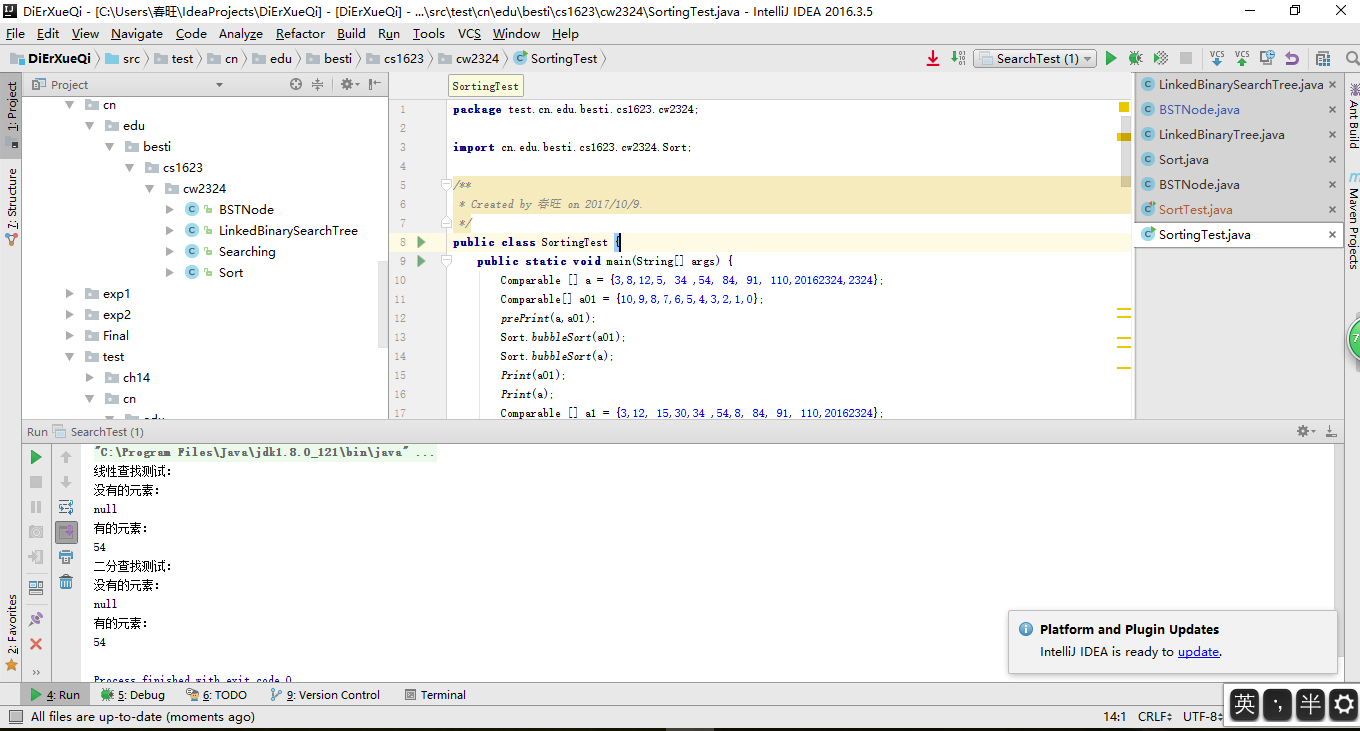
收获
在前个学期的学习过程中我们都在写产品代码,很少写测试代码,但是在这个学期的学习过程中我才渐渐的理解了测试代码的用处,没有测试代码,你的产品代码在你写下来的时候可能你觉得是对的,但是你一测试才会知道自己想的太简单,很多时候我们的产品代码都很难一次性写好,所以写好测试代码就可保证产品代码的正确性。
实验2
题目
重构你的代码
把Sorting.java Searching.java放入 cn.edu.besti.cs1623.(姓名首字母+四位学号) 包中
把测试代码放test包中
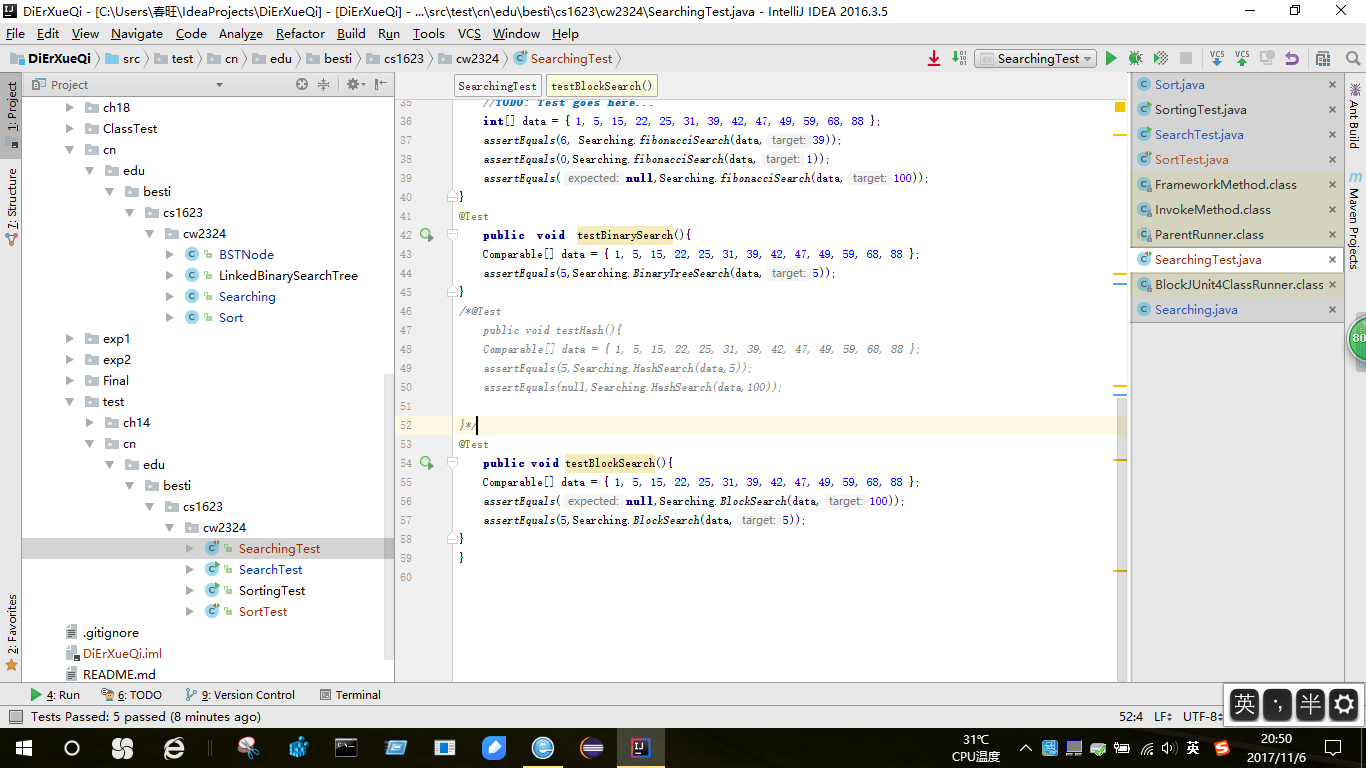
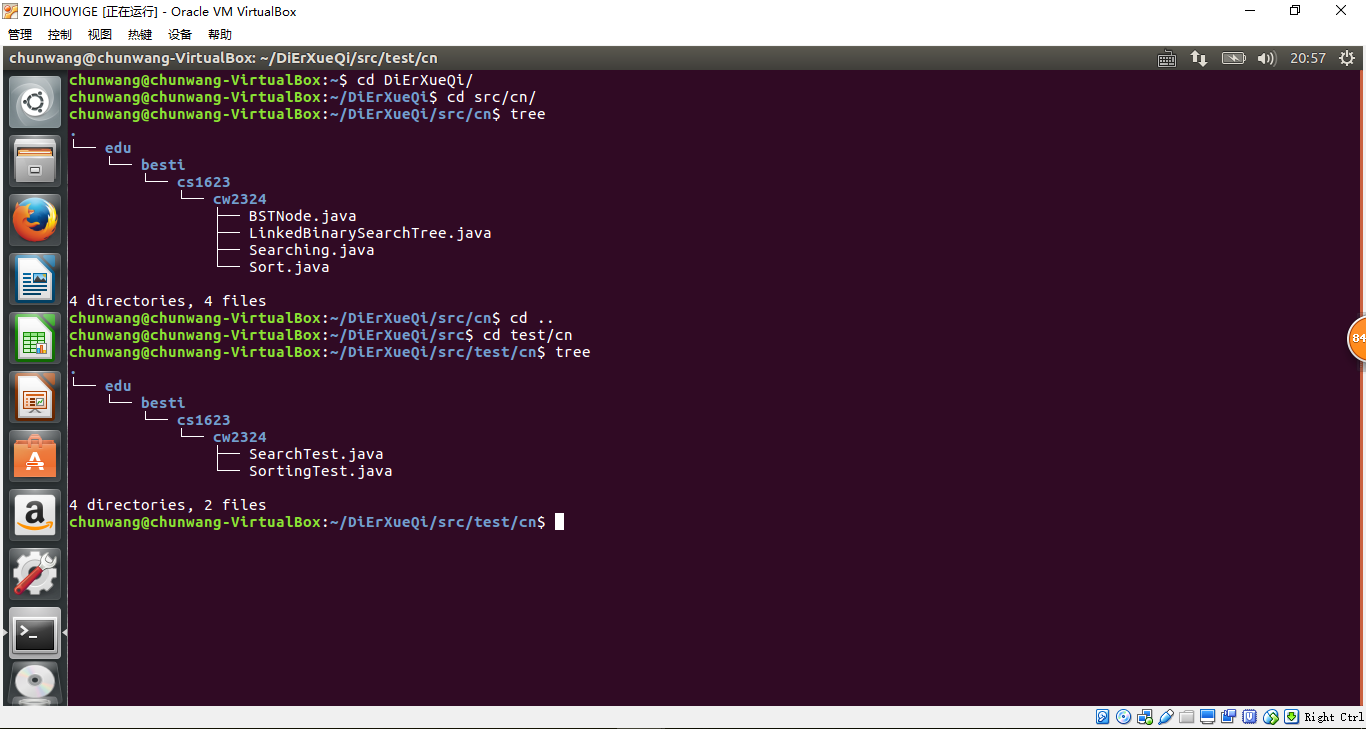
重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种)
代码与问题
重构就可让代码更加的简洁与直观,在IDEA中重构代码是比较简单的只需要用他自己带有的重构的菜单就可以了。在命令行下我就nachu了好久没有使用生物Linux系统的虚拟机来做实验,首先你要先建立一个文件夹,就要用到mkdir的命令,建好文件夹之后就是要将代码移入文件夹中就需要用到mv的命令但是要注意一点就是在mv命令运行的时候你要在原文件的目录和目的文件夹的共同的母文件夹底下运行才会成功,这一点需要注意,没注意就会很浪费时间去找原因。
在移动完文件之后,还没有完,因为不像在IDEA这样的集成开发文件他在移动的时候不会重构,所以移动之后就需要你去编辑代码里面的包名,才可以成功的重构,这一点就体现了集成开发环境的优点。
截图
实验3
题目
[参考笔记](http://www.cnblogs.com/maybe2030/p/4715035.html) 在Searching中补充查找算法并测试
提交运行结果截图
代码与问题
线性查找与二分查找
这个在以前的作业中已经实现就不再做介绍,问题之类也就不存在了
插值查找
这个算法是二分查找的进化的版本,二分查找在查找比较居中的元素的时候的确很快,但是比如在1-100的数字中找2或者99等比较靠近最值的元素时就比较的耗费时间,所以就有了插值插值,根据不同的元素来进行不同的划分,可能是三分四分甚至是更多。
类比二分查找将原先的二分的方法类比替换就可以:
mid = (first + last) / 2; // determine midpoint
mid =first + (first -last) * (target - data[first]) / (data[first] - data[last])//替换后的代码
斐波那契查找
首先我们先了解斐波那契数列{1,1,2,3,5,8,13,21,34}这个数列从第三个元素其每一个元素是前两个元素之和,在下面的时间过程就用到了这个性质,并且随着元素个数的增多S(n-1)/S(n)的值越来越接近0.618这个黄金比例,但是这一点在下面的实现过程中并不重要,重要的是之前提到的那个性质
public static Comparable fibonacciSearch(int[] data, int target) {
Comparable result = null;
int first = 0;
int last = data.length - 1;
int mid = 0;
int k = 0;// 斐波那契分割数值的下标
int i = 0; // 数组的元素个数
int[] f = fibonacci();// 构造斐波那契数列
///获取斐波那契分割数值下标
while (data.length > f[k] - 1) {
k++;
}
// 创建临时数组
int[] temp = new int[f[k] - 1];
//将所有的元素赋给临时数组
for (int j = 0; j < data.length;j++){
temp[j] = data[j];
}
// 因为在一个数组的元素的个数n = F[k]-1是才能用斐波那契查找所以要补全。
// 临时数组补充至f[k]个元素补充的元素值为临时数组的最后一个元素的值。
for (i = data.length; i < f[k] - 1; i++) {
temp[i] = temp[last];
}
while (first <= last) {
// 前半部分有f[k-1]个元素,由于下标从0开始
mid = first + f[k - 1] - 1;
if (temp[mid] > target) {
// 目标元素比参考元素小,向左查找,last的值变小
last = mid - 1;
//根据斐波那契数列特性 f[k] = f[k-1] + f[k-2]
// 因为右半部分排除所以就去掉了f[k - 2],所以 k = k-1
k = k - 1;
} else if (temp[mid] < target) {
// 目标元素比参考元素大,向右查找,first的值变大
first = mid + 1;
//根据斐波那契数列特性 f[k] = f[k-1] + f[k-2]
// 因为右半部分排除所以就去掉了f[k - 1],所以 k = k-2
k = k - 2;
} else {
// 如果为真则找到相应的位置
if (mid <= last) {
return mid;
} else {
// 出现这种情况是查找到补充的元素
// 而补充的元素与high位置的元素一样
return last;
}
}
}
return result;
}
// 构造斐波那契数列
public static int[] fibonacci() {
int[] finbonacci = new int[30];
int i = 0;
finbonacci[0] = 1;
finbonacci[1] = 1;
for (i = 2; i < 30; i++) {
// 后一个元素为前两个元素之和
finbonacci[i] = finbonacci[i - 1] + finbonacci[i - 2];
}
return finbonacci;
}
在上面的代码上我添加了详细的注释应该可看懂。
在实现时有一个要求就是要求元素个数是斐波那契数减一即使不够也要补齐之后才开始查找,我并不理解为什么要减一,而不是直接就是斐波那契数个元素呢?
后来我在一篇博客中找到了一个解释:
是为了格式上的统一,以方便递归或者循环程序的编写。表中的数据是F(k)-1个,使用mid值进行分割又用掉一个,那么剩下F(k)-2个。正好分给两个子序列,每个子序列的个数分别是F(k-1)-1与F(k-2)-1个,格式上与之前是统一的。不然的话,每个子序列的元素个数有可能是F(k-1),F(k-1)-1,F(k-2),F(k-2)-1个,写程序会非常麻烦。
二叉树树查找
二叉查找树我们在前一个实验中就已经实现过了,但是没有实现find方法,所以需要我们自己给查找树添加一个find方法来查找元素;
public T find(T target){
T re = null;
if (root.find(target).getElement() == target){
re = target;
}
return re;
}
这是添加的方法,随着这个方法的实现二叉树查找也就很容易实现了也就不再赘述了;
分块查找
分块查找算法是线性查找进一步的算法,最简便就是用来查找有序数列建序列划分为n份,之后用最大的元素作为索引来找元素,就大大降低了查找的次数。
public static Comparable BlockSearch(Comparable[] data ,Comparable target,int n){
int a = data.length / n;//每一部分包含的元素
Comparable result = null;
Comparable [] b = new Comparable [a];// 创建临时数组
for (int i = 0;i< data.length; i = i+ a){// 以每个组最小的元素为索引
if (data[i].compareTo(target) > 0){
int d = 0;
for (int j =i -a;j < i;j++){// 将目标组赋给临时数组
b[d] = data[j];
d++;
}
result = linearSearch(b,target);// 用线性查找来查找临时数组
break;
}
else if (data[i].compareTo(target) == 0){
result = data[i];
break;
}
}
return result;
}
在上面代码完成是出现最多的问题是循环的值边界问题很难出来一因为双重循环存在所以需要单步追踪是十分注意才能找到问题。
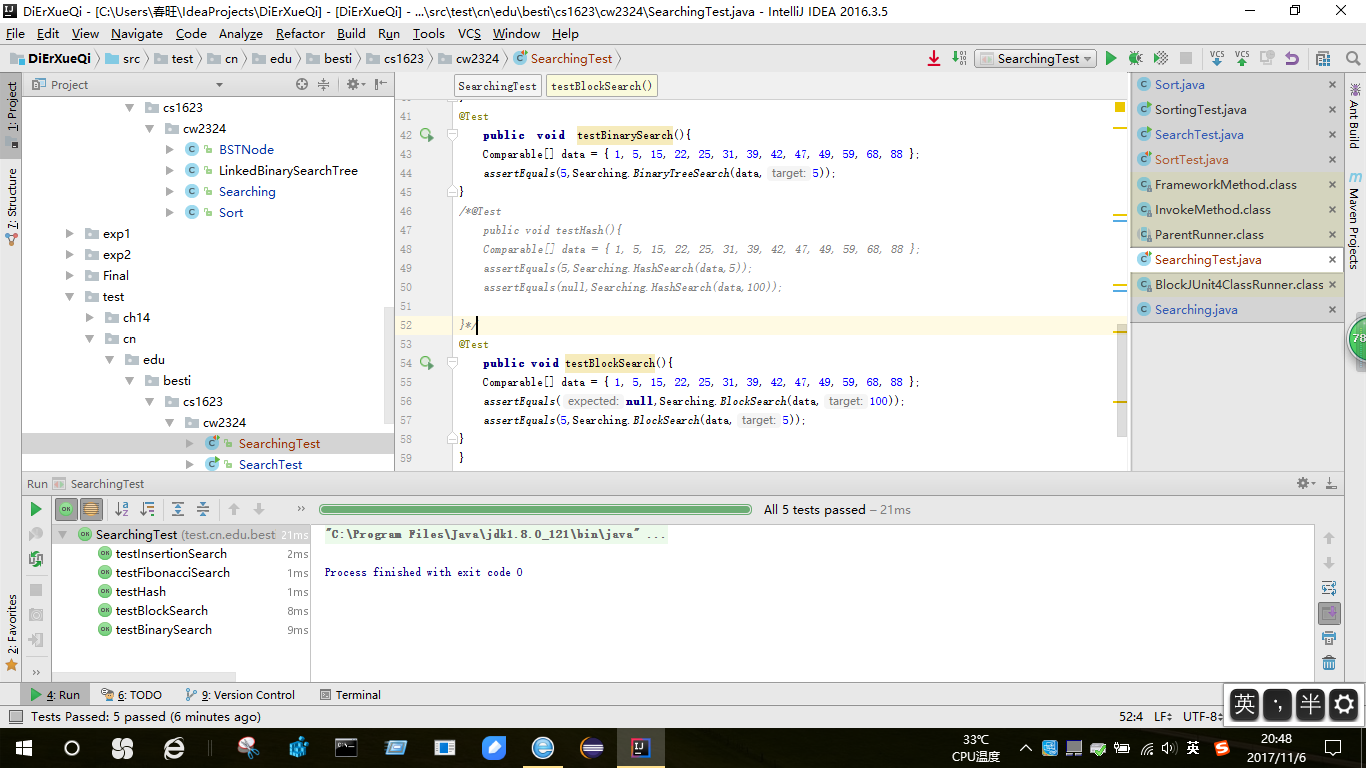
代码链接以上所有的代码都在Searching类中测试在test文件夹下的相同的路径下的测试类中。
截图
实验4
题目
补充实现课上讲过的排序方法:希尔排序,堆排序,桶排序,二叉树排序等
测试实现的算法(正常,异常,边界)
提交运行结果截图
推送相关代码到码云上
代码与问题
希尔排序
对于希尔排序我们先来看一个例子:
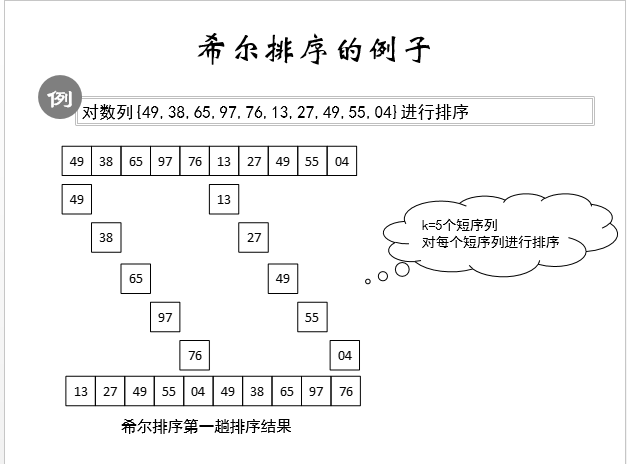
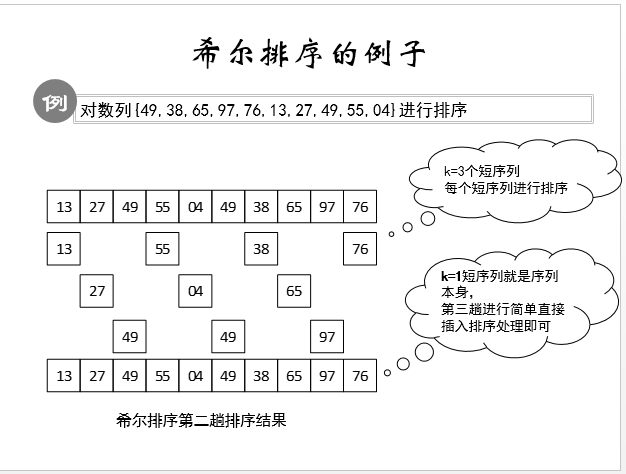
这个算法是插入排序的一个进一步的算法,大化小是算法简化的一个很重点的方法,这个算法就很好的利用了这一点。
二叉树排序
在我们原先创建的排序二叉树的性质中就有一条是排序二叉树的中序遍历就是二叉树的排序结果,所以在原先的基础上我们只需要将序列中的所有的数都添加到二叉树中之后,再获取他的中序遍历的形式就可以了。
对于代码我在代码上已经添加了比较详细的注释,在这里就不展示了。
堆排序与桶排序
这两个排序老师都在PPT中给出了代码并且附有详细的注释也就没有太大的问题。
代码链接以上所有的代码都在Sort类中测试在test文件夹下的相同的路径下的测试类中。
截图
实验5
题目
编写Android程序对各种查找与排序算法进行测试
提交运行结果截图
推送代码到码云
代码与问题
在这个实验中有比较多的界面课按键要去完善,同时不同的按键要打开不同的界面,在这一点上设计就会比较的麻烦,特别是按键的设立比较的花费时间。
截图
1.总的界面图
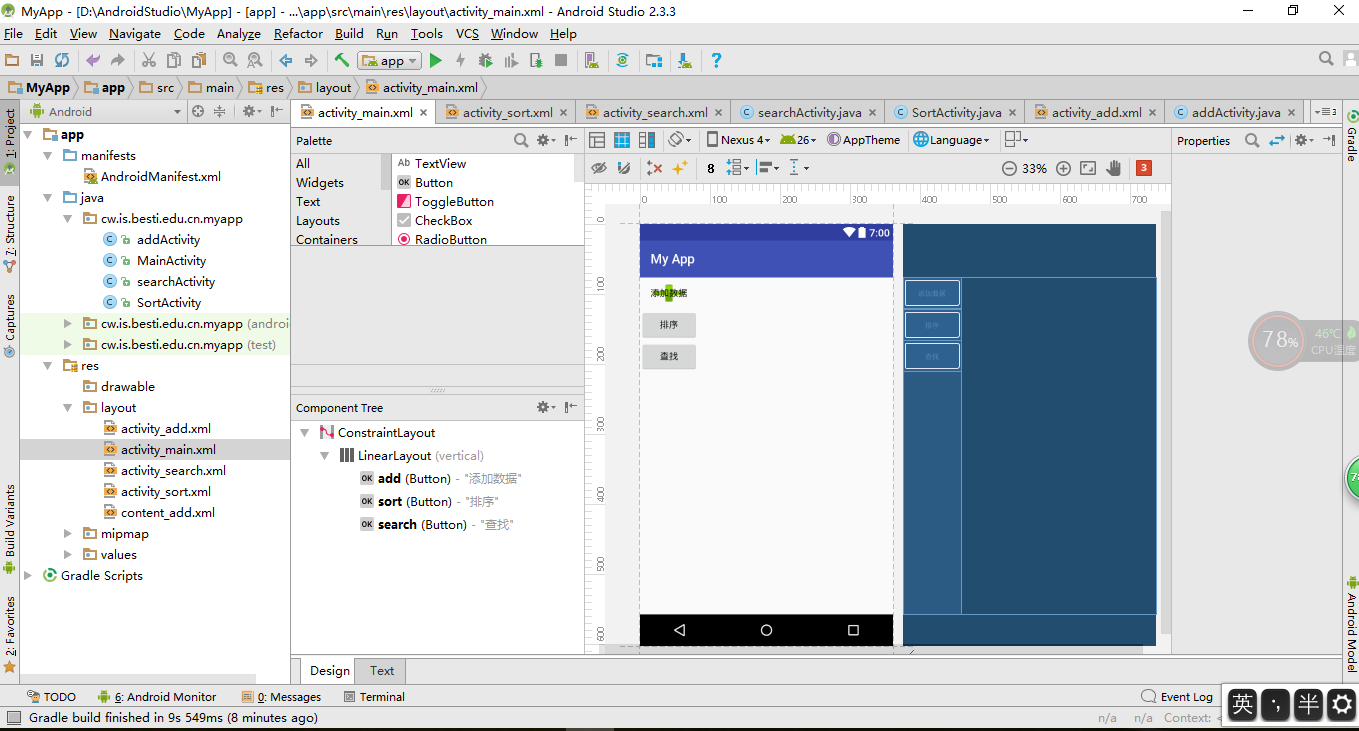
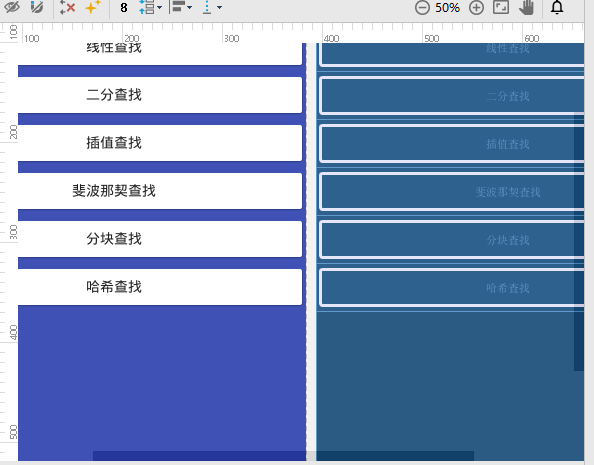
2.其他的各个小界面:



posted on 2017-11-11 13:05 20162324-春旺 阅读(526) 评论(2) 编辑 收藏 举报



