关于随机数的前世今生

首发于：洛谷日报#224

提起随机数，大家一定都不陌生。无论是在计算机科学领域，还是现实生活中，随机数的作用都不可小觑。

但随机数究竟是怎么一会事？它的作用是什么？它有事如何产生的？

本文会着重谈计算机的随机数以及产生算法，偏理论的只是会放到另一篇博客上随机数那些事

随机数定义及其性质

想要讨论随机数，首先应该明确一下随机数的定义。毕竟这个东西比较虚，并不像算法那样明确。在各大网上也没有给出很好的定义。

那...就不死抠定义了。

随机数一般来说符合下面这几个性质。

1. 它产生时后面那个数与前面的毫无关系

1. 给定样本的一部分和随机算法，无法推出样本的剩余部分

1. 其随机样本不可重现

另外还要说一下统计学伪随机数概念，划重点

统计学伪随机性。统计学伪随机性指的是在给定的随机比特流样本中，1的数量大致等于0的数量，同理，“10”“01”“00”“11”四者数量大致相等。类似的标准被称为统计学随机性。满足这类要求的数字在人类“一眼看上去”是随机的。（摘自百度词条）

实际上这也是在计算机中对伪随机数优劣的概念。

continue->

伪随机数

伪随机数，也就是我们c++中常用的随机数。为什么说它是“伪”随机呢？其实只要稍微详细的了解过c++ rand函数的人应该都能懂得这一点。

因为计算机本身并不能够产生和随机数，只能通过产生一组循环节很长的数来“伪造”随机。

c++的rand函数实际上只是根据你提供的种子计算出来的一组循环节很长的数。只要两次提供的种子是一样的，那么rand函数提供的随机数也是一样的。

可能有好奇的小伙伴就要问了，你说循环节很长，那到底长到什么程度呢？

经过不懈的努力，笔者成功弄到了rand()函数在LINUX系统下的实现：

static unsigned long next = 1;

/* RAND_MAX assumed to be 32767 */
int myrand(void) {
    next = next * 1103515245 + 12345;
    return((unsigned)(next/65536) % 32768);
}

void mysrand(unsigned seed) {
    next = seed;
}

（ 该代码摘自CSDN 原文链接）

通过这个算法我们可以推知，rand函数的循环节应该是在32768（2的15次方）以内。

（ 所以我白测试了是吗 ）

做这些测试实际上就是想说，在计算机方面。目前来说，如果不借助外部帮助，是无法达到真随机的。

计算机的随机数

计算机随机数的产生，我在讲伪随机时已经水过做过介绍了，也就不多说。

你以为我会帮忙把前面的代码拷过来吗？想太多了，自己翻页去。

（ 本来想放点图可能可以增加可读性，但好像放不了什么... ）

这里我主要想讲的是关于计算机在没有外界帮助下为什么不能产生真随机数。

真随机数的产生应该是与之前的数是没有任何关联的（ 论证过 ），那么在计算机中想对应的就是产生随机数的函数应该不需要调用任何参数（ 因为一旦调用了的参数，那么这个随机数的产生就会与参数相关 ）那么对于计算机来说，如何不调用任何参数并且产生不同的数呢？

这个...好像做不到。

这个换一个思维来解释好一点。因为计算机是一个绝对理智的存在，也就是说，计算机的一切行为都是可预测可推导的。而这恰恰违背了我们随机数标准中的第二条，即不可推断。对于计算机的任何程序，如果使用完全相同的参数来调用，它所输出的结果一定是完全一样的

农夫山泉不生产水，他们只是大自然的搬运工

计算机不生产数据，它只是数据的加工厂。

真随机数生成

不是重点，知道了就好。

真随机数生成器是一种通过物理过程而不是计算机程序来生成随机数字的设备。

这样的设备通常是基于一些能生成低等级、统计学随机的“噪声”信号的微观现象，如热力学噪声、光电效应和量子现象。这些物理过程在理论上是完全不可预测的，并且已经得到了实验的证实。硬件随机数生成器通常由换能器、放大器和模拟数字转换器组成。其中换能器用来将物理过程中的某些效果转换为电信号，放大器及其电路用来将随机扰动的振幅放大到宏观级别，而模拟数字转换器则用来将输出变成数字，通常是二进制的零和一。通过重复采样这些随机的信号，一系列的随机数得以生成。

（摘自百度词条原文链接）

随机数在OI中的常见应用

首先是用于检验程序。

估计这是大部分OIer的用法，拿一个随机数生成器去验证程序的速度,以及是否会RE（ 正确率是测不了的，毕竟自己手推答案比较慢 ）。

然后的话是某些算法的需要

这里因为算法太多，笔者也就大概介绍一下：

1. 大家熟悉的平衡树treap，它是通过生成随机权值引导进行旋转操作来使树接近平衡。

2. 相对常见的模拟退火就是随机算法的一个极致实现。它通过完全随机的操作变换解，使其不断接近正解。也是大家在OI中最多的用法。

3. 可能大家相对陌生的遗传算法中也有随机数的体现。主要表现在交叉和变异两方面上。

4. 可能大家听都没通说过的Pollard_Rho算法，就是超大数的分解质因数。因为数字过大无法用O（N）的算法。此时我们就通过随机数去“猜”质因数：不断生成随机值，判断是否出现两者之差为因子。（因为两者差为指定值的出现概率会比一个个猜大一倍），然后不断递归随机到的那个因子和那个数初一因子的另一半，直到找到质因子。具体算法比较复杂。有机会单独写一篇讲。模板题传送门

5. 然后与遗传算法类似的粒子群算法，随机主要出现在单个粒子的更新上。

6. 蚁群算法有用到，但因为过于冷门，就不多做介绍了。

（ 感觉随机数好像也就这么点用，在密码学统计学中用的比较多 ）

随机数优劣判定

在讲随机数算法之前，应该先讲讲随机数优劣的判定。

毕竟只有清除了随机数的优劣，我们才能说如何生成优质随机数。

在这里我们就要用到前面说的统计学伪随机性：

统计学伪随机性。统计学伪随机性指的是在给定的随机比特流样本中，1的数量大致等于0的数量，同理，“10”“01”“00”“11”四者数量大致相等。类似的标准被称为统计学随机性。满足这类要求的数字在人类“一眼看上去”是随机的。（我帮忙搬下来了）

结合计算机随机数的特性，我们能够得出以下三项判断随机数优劣的性质：

1. 随机程度，即随机算法是否足够复杂，随机数之间会不会存在明显联系。

2. 分布范围，即是否存在随机数在分布区域内大量出现偏大偏小的现象。分布是否足够平均。

3. 循环长度，即是否会在大量调用时很快地出现循环的情况。

有了这些评判规则，我们就比较好学习优质随机数的生成。

如何生成优质随机数

终于到了塞实货时间。

水不动了

这里前三个我讲一下在rand函数调用基础上自己做一点小操作来产生三种不同特性的随机数。

第四个专题讲MT19337算法（重点，绝对的重点），也就是目前优质随机数生成的普遍算法。

来回摆动式

这种随机数主要是针对退火算法之类的需要用随机数来修正答案的。

既然是修正答案，那么我们希望最好是来回摆动，一正一负的。

这种随机数的特点便是通过一部分人工处理，将原本的rand函数产生的随机数变成正负交替的。

int f  = 3000 ;
int change = 0.999 ; // f和change是用来控制随机数幅度不断变小的 
int con = -1 ;
int g = 1 ; // 控制正负交替 
int newrand ( ) {
	f *= change ;
	g *= con ;
	int tmp =  f * g * rand ( ) ;
	return tmp ;
}

这种随机数的产生引入了退火的思路，当然，你也可以直接使用算法中现成的温度来控制。

平均式

这种主要是用于平衡树treap的，特点就是在保证单个数随机的情况下在整体上保证分布比较平均。

实现原理也没什么好讲的，上代码就完事了。

int p ; // 希望的分布位置 
int newrand ( ) {
	int tmp =  ( p + rand ( ) ) / 2 ; // 通过取于分布位置的平均数，是产生的数更加靠近希望分布 
	return tmp ;
}

多次调用不重复式

当然，如果有人真的需要非常接近真随机的数。也就是多次运行程序也不会出现相同的情况。那就需要用到一定的外部干扰了。

首先是clock函数，上文已经说过，一个程序在不断调用期间。每一次的运行时间都会有细小的变化。我们就可以利用好这个变化。每次调用完后都重置一次随机数种子。

还有一个可能大家都会忽视的方法。计算机本身的误差。众所周知，计算机在做浮点运算时是会产生精度损失的，那么我们也可以利用这个特点辅助clock调整种子（毕竟程序调用时间相同其实可能性也不小，毕竟clock只精确到s/1000）。

int count ;
int realrand ( ) {
	count ++ ;
	int t = clock ( ) + 1 ; // 使用当前时间 
	for ( int i = 1 ; i < 12121307 ; i ++ ) { // 降速（如果放到具体代码里面使用可以将此参数调低） 
		t += rand ( ) ;
	}
	t += clock ( ) ; // 降速后扩大时间变化 
	t *= -1234 ;
	srand ( t * count + rand ( ) ) ; // 重置随机数种子 
	return rand ( ) ;
}

笔者经过大量实验，发现该函数前三个数出现重复几率相对会比较大（7~9%）建议从第四个开始使用。

上面的代码我并没用用精度损失来随机化，因为我发现同一个式子的进度损失值太小，以至于几乎不会发生什么改变，所以并没有使用。

随机数优劣度分析：

因为三个函数实际上都是在调用rand()函数，所以实际上他们的优质程度是与rand()函数相同的。记得我之前题的判断随机数优劣的标准吗？

1. 随机程度，即随机算法是否足够复杂，随机数之间会不会存在明显联系。

2. 分布范围，即是否存在随机数在分布区域内大量出现偏大偏小的现象。分布是否足够平均。

3. 循环长度，即是否会在大量调用时很快地出现循环的情况。

就是这个

我们来逐条分析。

首先，随机程度方面，虽然你们之前看过rand()函数代码，可能清楚数字之间的关联
。但在实际运用中，这个数字之间的关联还是基本可以忽略的。所以在随机程度方面，rand()函数还是能够勉强通过的。

在平均分布方面，单看代码可能感觉不出来。

那么，笔者就做一个测试：

#include<iostream>
#include<stdlib.h>
using namespace std ;
int data[1000] ;
int main ( ) {
	for ( long long i = 1 ; i <= 100000000 ; i ++ ){
		int tmp = rand ( ) % 100000 ; //生成一个100000以内的随机数 
		data[ tmp / 10 ] ++ ; //统计出现次数 
	}
	for ( int i = 1 ; i <= 100 ; i ++ ) {
		cout << data[i] << endl ;
	}
	cout << " ok " << endl ;
	return 0 ;
}

最后结果：

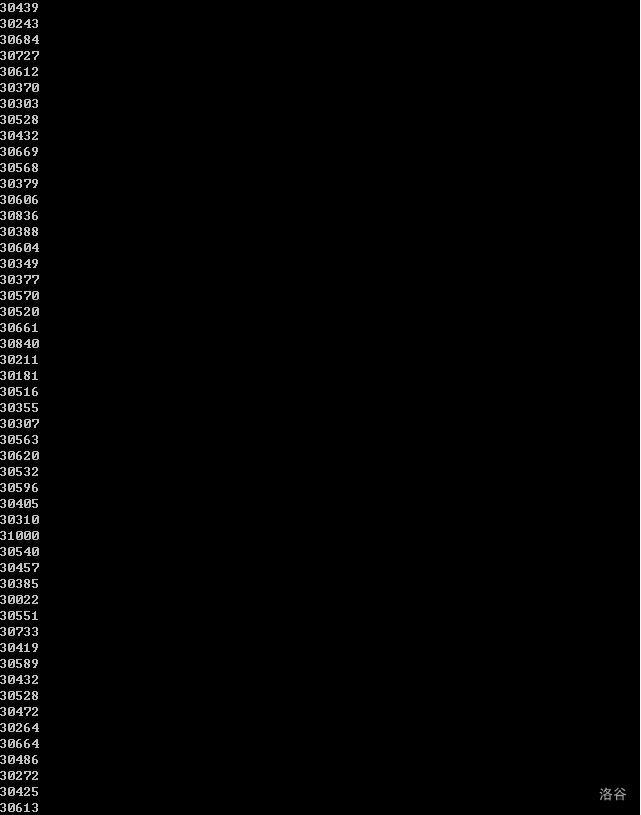
从中我们可以看到，这个分布还是非常平均的。

循环长度...

这个主要就是rand()函数的硬伤了，32768这个长度真的挺不够用的。在需要大量调用rand()函数的算法中（比如退火），基本都会把rand()卡出循环。

那有没有既优质又循环节长的算法呢？

梅森旋转算法（MT19337）

这个很重要，所以标题升了一级

这个是目前产生优质伪随机数的普遍算法

在C++11，python等多种语言中都有使用# 旋转算法简介

梅森旋转算法，也可以写作MT19937。是有由松本真和西村拓士在1997年开发的一种能快速产生优质随机数的算法。

其实这个算法跟梅森没有什么关系，它之所以叫做是梅森旋转算法是因为它的循环节是2^19937-1，这个叫做梅森素数。

这个算法之所以说是产生优质随机数，是因为它在循环节特别长的情况下（2^19337-1）还能保证平均分布。

可能有的同学对这个循环节有点质疑。可能觉得2^19937-1有点短？

我在这里大概给一个概念：

银河系中的恒星数量级10^11

撒哈拉沙漠中的沙子数数量级是10^26

宇宙中目前可观察的粒子数量级是10^87

2^{19937数量级是10}6001

这个比较大概心里有数了吧

相差的已经不止是一个数量级了

同时他在623维中的分布都十分的均匀（这个不用理解）

知道分布平均就好了

（梅森镇楼）

->continue

前置知识

分析这个算法的原理需要的前置知识在网上讲的都比较绕，我在这里就通俗的科普一下，主要是认识这几个名词。

（用词不准确轻喷）

线性反馈移位寄存器（LFSR）

这个，就当它是随机数发生器就完事了，不要太去纠结定义。后面会讲。

本原多项式

简单的说来就是没法化简的多项式

比如 $y=x^4+x2$ 就可以化简为$( x^2 + 1) x ^ 2$

也是知道就好，不用过于追求定义

级

计算机的一个二进制单位（0或1）就是一级

这个应该比较好理解

反馈函数

这个应该是网上看别的博客最绕的知识点

简单地理解成你要对这个寄存器干什么的一个函数就好了

（看到这里应该还没懵吧）

异或

这个...

还要我科普吗？

就是两个数，如果都是0或都是1就输出0，一个1一个0输出1.

->continue

原理分析

这个旋转算法实际上是对一个19937级的二进制序列作变换。

首先我们达成一个共识：

一个长度为n的二进制序列，它的排列长度最长为2^n。

当然这个也是理论上的，实际上可能因为某些操作不当，没挺到2^n个就开始循环了。

那么如何将这个序列的排列撑满2^n个，就是这个旋转算法的精髓。

如果反馈函数的本身+1是一个本原多项式，那么它的循环节达到最长，即2^n-1

这个数学证明本文不作过多论述，有兴趣者可以自己查阅资料

个人感觉单讲知识点挺难懂的（笔者就是这么被坑的）

我们就拿一个4级的寄存器模拟一下：

我们这里使用的反馈函数是 y=x^4+x2+x+1（这个不是本原多项式，只是拿来好理解）

这个式子中x^4,x2,x的意思就是我们每次对这个二进制序列的从后往前数第4位和第2位做异或运算 ，然后x的意思是我们再拿结果和最后一位做异或运算。把最后的结果放到序列的开头，整个序列后移一位，最后一位舍弃。

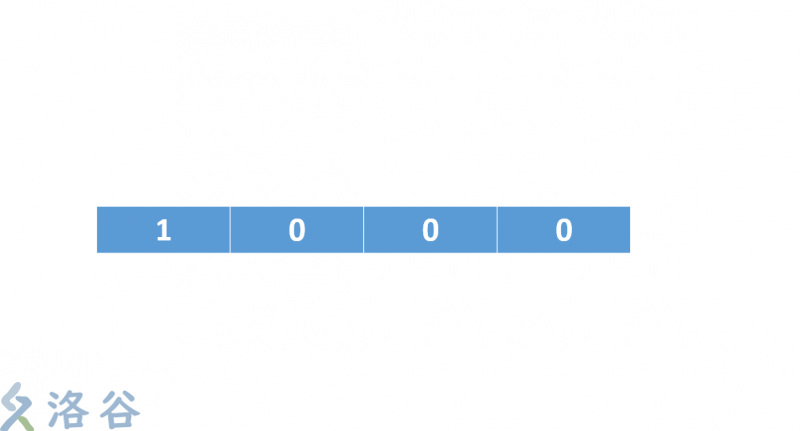
1. 初始数组 { 1 ， 0 ， 0 ， 0 } （为什么不是 0，0，0，0 你们可以自己想想，文章末尾揭晓）

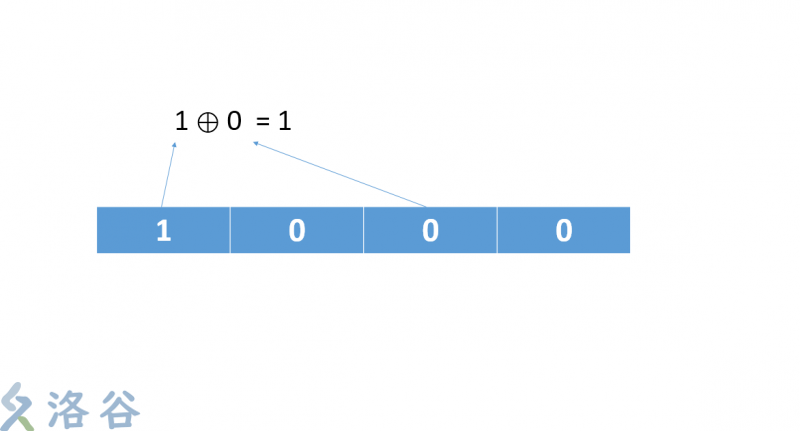
2. 将它的第四位和第二位抓出来做异或运算

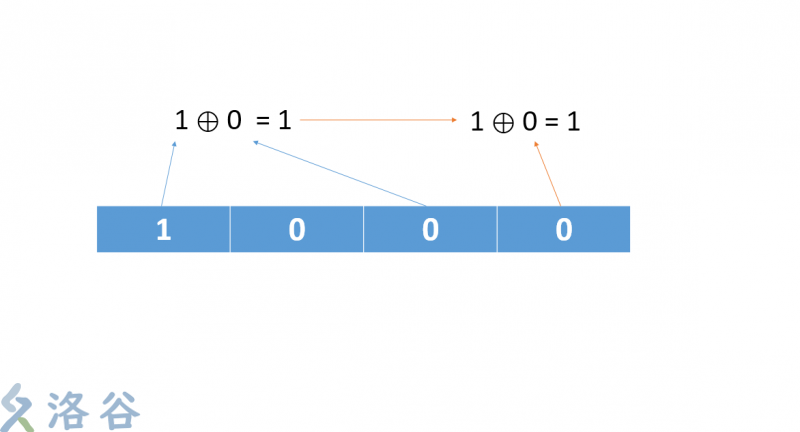
3. 把刚刚的运算结果和最后一位再做一次运算

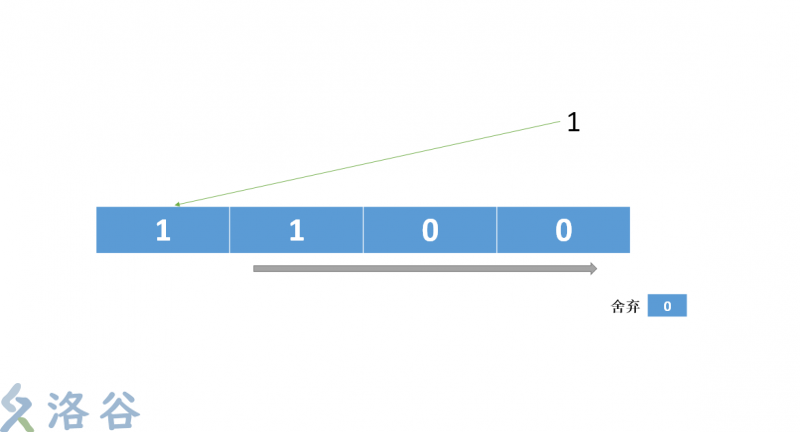
4. 把最后的运算结果放到第一位，序列后移。最后一位被无情的抛弃

这就是一次运算，然后这个算法就是不断循环这几步，从而不断伪随机改变这个序列。

上图是一个网上找的一个4级寄存器的模拟过程

大家可以推一下，它所使用的反馈函数（y=x^4+x+1）

因为这个是本原多项式

所以他最后的循环节是2^4-1=15

运算结果如下：

（图片摘自原文链接）

大家可以看到这个运算结果包含到了2^4-1~1中的所有数字，并且没有循环。

同时拥有很好的随机性。

可能又有人有疑问了：

这个运算结果明明能看出规律啊，我不是看到了很多1的平行四边形吗？

醒醒

这是二进制数。

如果你把它转化成数字。

8 12 14 15 7 11 ...

能看出规律？

关于旋转

可能有人到这里还没看出“旋转”在哪里。

因为我们每次计算出来的结果会放在开头，序列后移一位。看起来就像数组在向后旋转...

（本来想做gif的，后来不知道怎么做出旋转）

大家自行脑补

->continue

算法评价

1.随机程度：

这个应该不用说了，认真看这个原理的都应该清楚它的随机程度比rand（）不知道高到哪里去了。如果说rand（）还能够用公式表达的话，这个19337已经无法通过算式表达了。

2.分布范围：

这里笔者比较懒就不做证明了。有兴趣的可以拿上面的代码自行检测。

3.循环长度：

其实这点我可以直接跳过的。19337算法最不慌的就是循环长度。2^19337的循环长度根本不需任何算法。毕竟人家这个算法的循环长度是与空间大小成指数级关系的……

代码实现

（笔者很懒，直接搬原代码出处的代码）

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <time.h>

using namespace std;

bool isInit;
int index;
int MT[624];  //624 * 32 - 31 = 19937


随机种子
void srand(int seed)
{
    index = 0;
    isInit = 1;
    MT[0] = seed;
    for(int i=1; i<624; i++)
    {
        int t = 1812433253 * (MT[i-1] ^ (MT[i-1] >> 30)) + i;
        MT[i] = t & 0xffffffff;   //取最后的32位
    }
}


梅森旋转
void generate()
{
    for(int i=0; i<624; i++)
    {
        // 2^31 = 0x80000000
        // 2^31-1 = 0x7fffffff
        int y = (MT[i] & 0x80000000) + (MT[(i+1) % 624] & 0x7fffffff);
        MT[i] = MT[(i + 397) % 624] ^ (y >> 1);
        if (y & 1)
            MT[i] ^= 2567483615;
    }
}

输出函数
int rand()
{
    if(!isInit)
        srand((int)time(NULL));
    if(index == 0)
        generate();
    int y = MT[index];
    y = y ^ (y >> 11);
    y = y ^ ((y << 7) & 2636928640);
    y = y ^ ((y << 15) & 4022730752);
    y = y ^ (y >> 18);
    index = (index + 1) % 624;
	return y;  //笔者注：y即为产生的随机数 
}

int main()
{
    srand(0);  //设置随机种子
    int cnt = 0;
    for(int i=0; i<1000000; i++)  //下面的循环是用来判断随机数的奇偶概率的 
    {
        if(rand() & 1)
            cnt++;
    }
    cout<<cnt / 10000.0<<"%"<<endl;
    return 0;
}

->continue

填一下前面的坑

这里回答一下前面的那个问题：

为什么循环节是2^{n-1而不是2}n

这个问题的答案和为什么初始序列不能是 { 0 , 0 , 0 , 0 }是一样的，因为如果全是0的话，无论怎么异或运算都不能产生循环。那么还怎么伪随机啊。

因为不能是全0，所以循环节要-1

最后非常感谢你能有耐心读到这里。

本文到这里应该就 水完 结束了，当然，既然你好不容易看到了这里，我就给一个彩蛋吧（ 有点勉强 ）。

关于rand函数为什么是用1103515245和12345这两个数...你可以理解为玄学。 不过真是原因是用这两个数推算出来的的随机数分布相对平均。更符合伪随机数的特性。（ 这个我尽力用实验来论证，目前还在构思，也可能正在实验 ）

感谢@qbu666666和@dgklr大佬对本文文字错误以及论述缺陷的指出。

然后特别感谢一下@MZW_BG对本文真随机部分的提醒以及帮助。

大家都很强，可与之共勉。