HL20220815T4

题解

题意

思路

首先建立一棵最短路树，提取出从s到t的最短路

假设她删的不是最短路上的边，那答案就是原来的最短路

接下来考虑删的边在最短路上的贡献

我们首先对最短路上的点编号

加入删除的是这条边

我们需要越过这条边，即从边左边的点到边右边的点

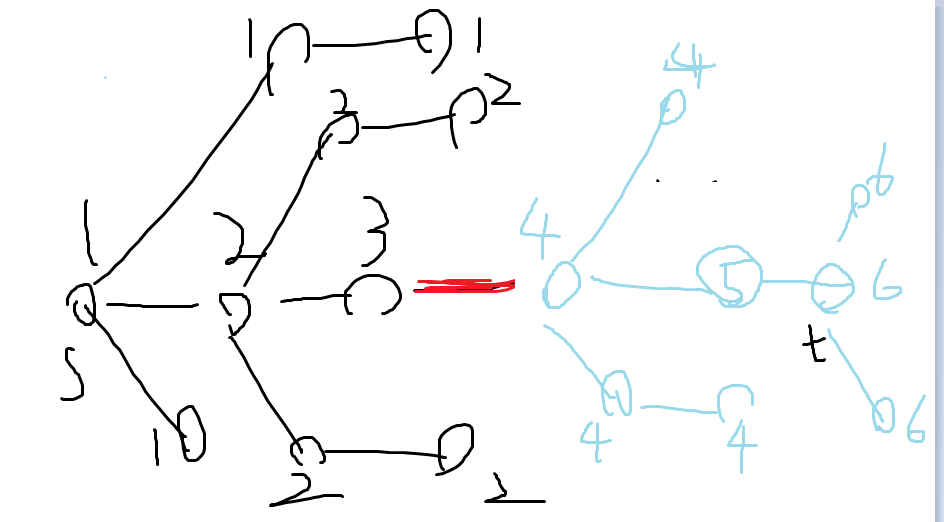
即从黑色点不经过红色边到蓝色点

考虑对黑色点求出从s到它的最短路，对于蓝色点求出从t到它的最短路

如果存在(u(黑色点),v(白色点),w)这条边，则它会对答案贡献\(dis_s[u]+dis_t[v]+w\)

接下来考虑怎么快捷的维护它

为了方便维护答案，我们对边进行新的编号

现在我们已经有一条满足条件的橙色边

考虑它会在哪些边删除时贡献

在2号边、3号边被删除时它会贡献答案

也就是对一个连续的区间产生贡献

为了方便的统计答案，我们对点进行了编号

仔细观察一下点的编号，我们可以方便得出区间的范围

用线段树区间修改，单点查询就好

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mkp make_pair
#define x first
#define y second
const int N=2e5+5;
const ll inf=1e18;
ll dis[2][N],c[N<<2],tag[N<<2],rec;
pair<int,int>pre[2][N];
int vis[N],n,m,head[N],edgenum,s,t,use[2][N],bel1[N],bel2[N],in[N],q,a[N];
struct edge{int v,next,w,id;}e[N<<1];
void add(int u,int v,int w,int id){
	e[++edgenum]=edge{v,head[u],w,id};
	head[u]=edgenum;
}
#define pli pair<ll,int>
priority_queue<pli,vector<pli>,greater<pli> >que;
void dij(int s,int id){
	for(int i=1;i<=n;i++)dis[id][i]=inf,vis[i]=0;
	dis[id][s]=0;que.push(mkp(0,s));
	while(!que.empty()){
		int u=que.top().y;que.pop();
		if(vis[u])continue;vis[u]=1;
		for(int i=head[u],v;i;i=e[i].next)
			if(dis[id][v=e[i].v]>dis[id][u]+e[i].w){
				pre[id][v]=mkp(e[i].id,u);
				dis[id][v]=dis[id][u]+e[i].w;
				que.push(mkp(dis[id][v],v));
			}
	}
	int u=t;
	while(u!=s){
		use[id][pre[id][u].x]=1;
		u=pre[id][u].y;
	}
}
void dfs1(int u,int tp){
	bel1[u]=tp;
	for(int i=head[u],v;i;i=e[i].next)
		if(dis[0][v=e[i].v]==dis[0][u]+e[i].w&&!in[v]&&!bel1[v])
			dfs1(v,tp);
}
void dfs2(int u,int tp){
	bel2[u]=tp;
	for(int i=head[u],v;i;i=e[i].next)
		if(dis[1][v=e[i].v]==dis[1][u]+e[i].w&&!in[v]&&!bel2[v])
			dfs2(v,tp);
}
void pudo(int x){
	if(tag[x]!=inf){
		c[x<<1]=min(c[x<<1],tag[x]);
		c[x<<1|1]=min(c[x<<1|1],tag[x]);
		tag[x<<1]=min(tag[x<<1],tag[x]);
		tag[x<<1|1]=min(tag[x<<1|1],tag[x]);
		tag[x]=inf;
	}
}
void puup(int x){c[x]=min(c[x<<1],c[x<<1|1]);}
void build(int x,int l,int r){
	c[x]=tag[x]=inf;
	if(l==r)return;
	int mid=(l+r)>>1;
	build(x<<1,l,mid);
	build(x<<1|1,mid+1,r);
}
map<pair<int,int>,int>mp;
void change(int x,int l,int r,int L,int R,ll w){
	if(l>=L&&r<=R){
		c[x]=min(c[x],w);
		tag[x]=min(tag[x],w);
		return;
	}
	int mid=(l+r)>>1;pudo(x);
	if(mid>=L)change(x<<1,l,mid,L,R,w);
	if(mid+1<=R)change(x<<1|1,mid+1,r,L,R,w);
	puup(x);
}
ll ask(int x,int l,int r,int p){
	if(l==r)return c[x];
	int mid=(l+r)>>1;pudo(x);
	if(mid>=p)return ask(x<<1,l,mid,p);
	return ask(x<<1|1,mid+1,r,p);
}
int main(){
	freopen("graph.in","r",stdin);
	freopen("graph.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1,u,v,w;i<=m;i++){
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w,i);add(v,u,w,i);
		mp[mkp(u,v)]=i;mp[mkp(v,u)]=i;
	}
	scanf("%d%d%d",&s,&t,&q);
	dij(s,0);dij(t,1);int u=t;m=0;
	while(u!=s){a[++m]=u;in[u]=1;u=pre[0][u].y;}
	a[++m]=s;in[s]=1;
	for(int i=1;i<=m/2;i++)swap(a[i],a[m-i+1]);
	for(int i=1;i<=m;i++)dfs1(a[i],i);
	for(int i=m;i>=1;i--)dfs2(a[i],i);
	build(1,1,m);
	for(int i=1;i<=n;i++)
		for(int j=head[i],v;j;j=e[j].next){
			v=e[j].v;
			if(bel1[i]<=bel2[v]-1&&(bel1[i]+1!=bel2[v]||e[j].id!=pre[0][v].x))change(1,1,m,bel1[i],bel2[v]-1,dis[0][i]+dis[1][v]+e[j].w);
		}
	for(int u,v;q--;){
		scanf("%d%d",&u,&v);rec=inf;
		if(bel1[u]>bel1[v])swap(u,v);
		if(!use[0][mp[mkp(u,v)]])rec=dis[0][t];
		else rec=ask(1,1,m,bel1[u]);
		if(rec==inf)puts("Infinity");
		else printf("%lld\n",rec);
	}
}