并查集算法

这几天博主在看并查集算法，整理了一下：

我自己花了几个图，不好看大家将就一下，欢迎大家评论留言探讨学习。

这个班级有1,2,4三位同学，开始他们谁都不认识谁，但是毕竟都是同学总是要混个脸熟不是？

 

    public void union(int n,int m) {
        n=find(n);
        m=find(m);
        if(n!=m) 
            friend[n]=friend[m];
    }
    public int find(int n) {
        if(friend[n]==0) 
            friend[n]=n;
        return friend[n];
    }    

开始啊，1他谁都不认识，但是他可以推销自己，也就是friend[1]他就是1，2也是这个样子，两个人成为朋友总要有个人先开口，这不就2先开口了，那么friend[2]=friend[1]，也就是2认识1了。

变成了这样：

 

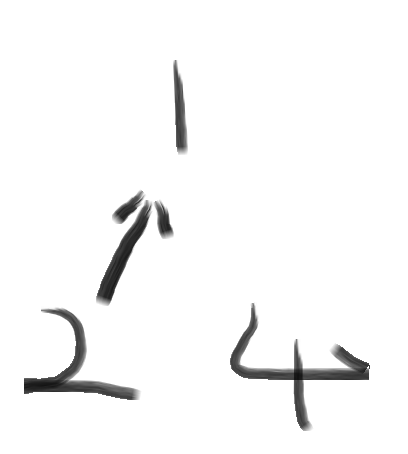
后来啊这个班里的同学都认识了，成为了一个小圈子，但是年级里还有别的班级，这个时候出现了班级B：

 

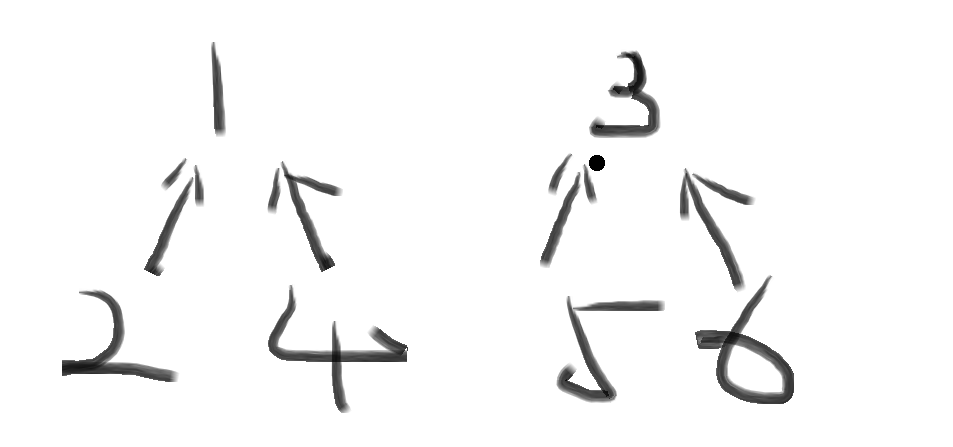
班级A的代表是1，班级B的代表是3。这一天4和5这两个小同学吧眉来眼去他们呢好上了，他们就想着让自己的朋友也都彼此认识一下，这个时候出现了状况，friend[4]本来是1了，friend[5]是3了，怎么可以让他们都成为同一个代表呢？5是男孩子他就去找了他的联系人3，而3恰好就是班级B的老大，3觉得既然以后是朋友了，我让你1当老大也没什么。于是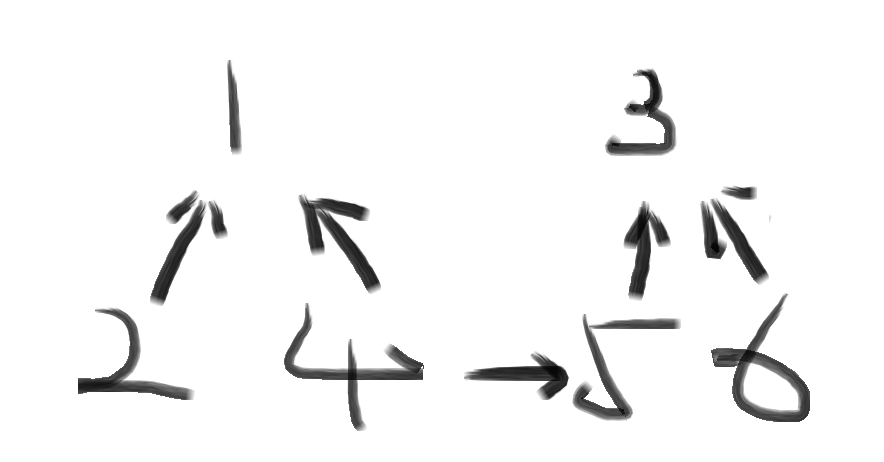

本来应该是这个关系的顺序，因为4不想新认老大变成了这样！

    public void union(int n,int m) {
        n=find(n);
        m=find(m);
        if(n!=m) 
            friend[n]=friend[m];
    }
    public int find(int n) {
        if(friend[n]==0) 
            friend[n]=n;
        else {
            int x=friend[n];
            if(friend[n]!=n)
                friend[n]=find(x);
        }
        return friend[n];
    }

这个时候他们就处在同一个圈子里了。

但是吧，5和3说这件事的时候呢，6不在场，所以6的标记还是3。

也就是6->3->1这条路并没有遍历过，反观5->3->1已经遍历过了，所以5的编号已经是1，6却只能等有人需要从他这里认识他的联系人的时候，他才能变成1，也就是直接汇报。