hdu2089——不要62（数位DP模板题）c++
前言
——题目链接——
hdu2089
感觉其他人的题解里有很多东西并没有解释清楚，搞得我到处都是问题，做出来后打算自己写一个非常清晰的题解。
所有的东西都是我自己的理解，可能会有不太正确的地方。
如有雷同，算你抄我的
思路解析
非常经典的一道数位DP水题，
首先讲一下数位DP思路：
DP我们一般都是在数组上做推算，
而数位DP就是在数的每一位数字上进行DP。也就是从第一位数字推第二位数字，再从第二位数字推第三位数字，以此类推。
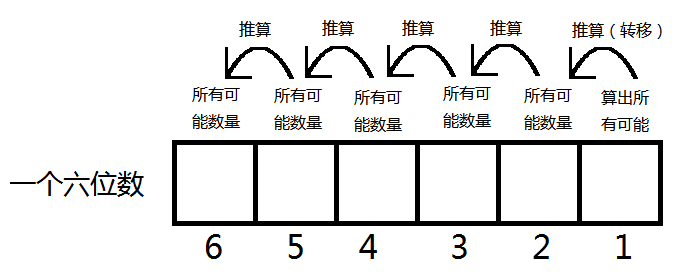
数位DP的题比较明显，一般都是在数上有些要求。
我们规定dp[i][j]表示：数的第i位为j时一共有多少种情况符合题目要求。（注意这里的dp[i][j]不包含第i位往上的情况）
DP转移方程
显然，我们可以得出转移方程为dp[i][j]+=dp[i-1][k]（0≤k≤9）。
因为它当前第i位的可能数量就是所有它上一位的可能数量之和。
比如3XXX的所有可能就是30XX、31XX、......、39XX这些数量的和。简化了就是0XX、1XX、......、9XX这些的和。（可以简化是因为当前位对上一位没有影响）
当然转移是有条件的。这道题要求数上的数字不能是4和连续的62，4可以理解为第i位不能是4，而62可以理解为数的当前第i位和第i-1位不能是6和2。（i-1比i位单位小，而且是i位的上一位）
所以只要特判第i位为4或者第i位为6时且上一位2时continue就行了。
我们可以先将dp数组初始化。
整个dp数组初始化如下：
void init()//因为不会因输入的数而被影响，所以可以提前进行初始化 { dp[0][0]=1;//初始值 for(int i=1;i<=7;i++)//看数据范围，从1位数到7位数 { for(int j=0;j<=9;j++) { if(j==4) continue; for(int k=0;k<=9;k++)//枚举上一位的所有可能的值 { if(j==6&&k==2) continue; dp[i][j]+=dp[i-1][k]; } } } }
结果输出
（其实我觉得这部分才是最难的。。。）
数位DP的输出需要进行特殊操作。
由于题目要求一个准确的区间，而我们的dp数组存的是1~n的值，所以要进行分位取值。
具体过程如下：
一个六位数362415，
首先看第一位3：它是第6位，我们可以把它拆分成许多个数相加：000000~099999+100000~199999+200000~299999+300000~362415。
所以它就等于dp[6][0]+dp[6][1]+dp[6][2]+300000~362415
所以对于第i位为j时，我们就要计算sum+=dp[i][0]+dp[i][1]+......+dp[i][j-1]。
那后面的300000~362415呢？
因为它的第六位只会为3，不会对后面造成影响。
我们可以把它再看成一个五位数62415，并继续按照上面的操作累加sum。
以此类推。。。
但算最后一位的时候，我们会把sum加上1、2、3、4的dp值而不包括5，所以这个方法它求的是1~(n-1)中的情况数量。
因为dp数组中都是存的1~n的值而输出的是区间，所以对于区间[l,r]来说，只需求出1~r的情况数量再减去1~(l-1)的情况数量就可以了。
又因为返回值是1~(n-1)的答案，所以应该输出r+1的情况值减去l的情况值。（说的有点绕，不过用下面的结论就好了。）
printf("%d\n",answer(m+1)-answer(n));
但要注意：
1.如果当前位为4，则需要算完dp[i][0]+......+dp[i][j-1]后再判断退出。（因为含有4的话后面都是不合理的，不用计算）
2.如果下一位(i+1)是6且当前位是2，则跟上面一样判断完退出。（同上）
3.注意62需要在计算dp[i][0]+......+dp[i][j-1]中特殊判断一下。如果数的上一位是6时，则当前第i位时不可以是2的。
int answer(int x) { int l=0; while(x) { a[++l]=x%10;//将x的每一位存下来 x/=10; } a[l+1]=-1;//由于有多个数据，所以要将第i+1位赋值-1以避免错误判断。 int sum=0; for(int i=l;i>=1;i--) { for(int j=0;j<a[i];j++)//枚举当前位的所有可能的值 { if(a[i+1]==6&&j==2) continue; sum+=dp[i][j];//总和 } if(a[i]==4) break; if(a[i+1]==6&&a[i]==2) break; } return sum; }
最后
只需要注意一下输入都是0的时候退出。（其实我感觉这句是废话）
if(!n&&!m) return 0;
我总结一下那些我觉得可能会WA的点，主要就是求结果的那里（前面都提到过）：
1.求结果时j不能取a[i]。
2.求结果时判定4和62一定要放到求和后面。
3.求结果时第l+1位要赋-1。
最终代码就不放了，能看懂的自然会写。（其实就是个输入输出加调用函数）
感谢你能看到这里，谢谢。
