Hough变换原理
Hough变换
-
基于点-线的对偶思想
-
\(y=px+p\Rightarrow p=-px+y\)
-
对于一个图像坐标系下的点，我们可以把它变成参数坐标中的线
-
对于一个图像坐标系下的在同一直线上的一组点，我们把它变成参数坐标系下经过同一点的多条直线
-
对于图像坐标系下的一条直线，我们把它变成参数坐标系下的一个点
-
图像坐标系下多个点在一条直线上\(\Rightarrow\) 参数坐标系下多条直线交于同一个点
-
-
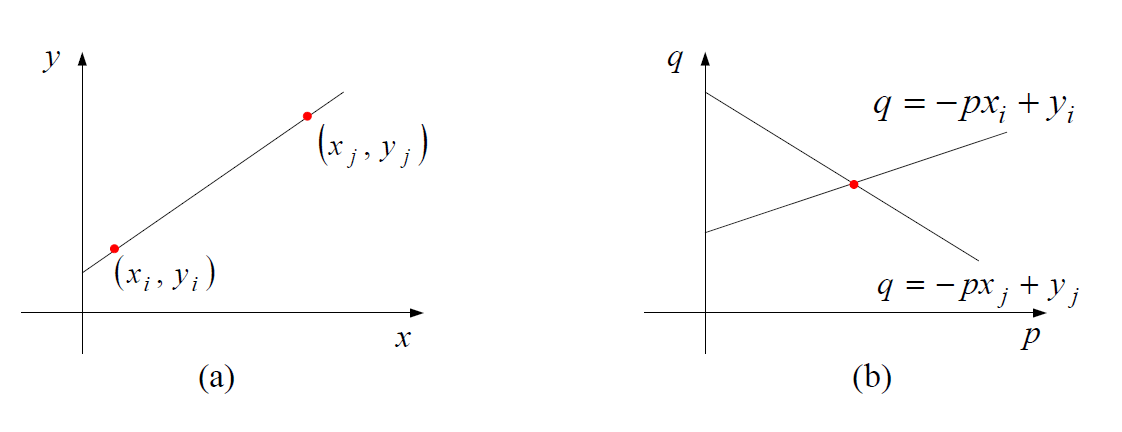
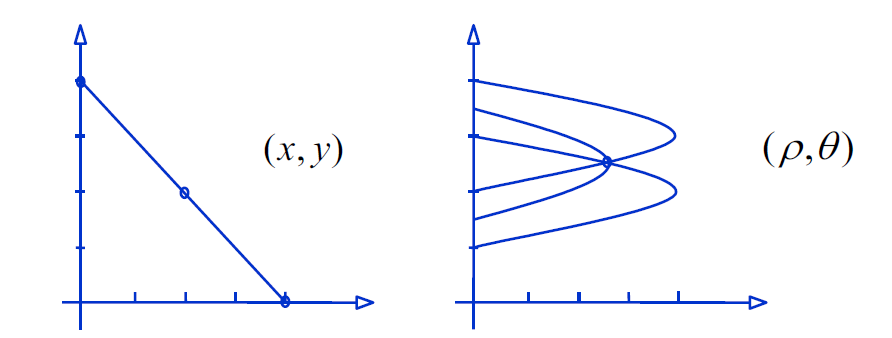
现在把之前的参数方程变成极坐标的参数方程
-
这样做的好处是让原本无界的直线变得有界
-
图像空间中的点\(\Rightarrow\) 参数空间上的曲线
-
那么图像空间下多个点共线的问题就变成了参数空间下多个曲线有交点
-
-
算投票
-
就是如何算几条曲线的交点
-
方法
-
曲线上的每个点都能投一票
-
交点自然是得票数最大的
-
-
-
hough实现具体步骤（直线）
-
建立一个参数（λ，θ） 空间的二维的数组，该数组相当于一个累加器
-
顺序搜索图像中所有目标(黑色)像素，对于每一个目标像素，在参数空间中根据式(3)找到对应位置，然后在累加器的对应位置加 1
-
求出参数空间(累加器)中最大值，其位置为（λ'，θ'）
-
通过参数空间位置（λ'，θ'） ，根据式(3)找到图像空间中相对应的直线参数。
-
-
圆弧检测
-
给定一个圆弧，它会有三个参数：两个参数确定圆心，一个参数确定半径
-
具体实现步骤
-
建立参数空间
-
初始化累加器
-
计算图像空间中边缘点的梯度幅度\(G_{mag}(x,y)\)和角度\(\theta (x,y)\)
-
若边缘点参数坐标满足\(b=atan\theta -xtan\theta +y\)，则该参数坐标对应的累加器加1
-
拥有最大值的累加器所在的坐标即为图像空间中的圆心位置
-
得到圆心坐标后，易得\(r\)
-
-
参考资料
https://blog.csdn.net/h532600610/article/details/52983490
老师的PPT
