2025.1.5 闲话 (2)

歌：プラネットヒーロー - 打打だいず + irucaice feat. 初音ミク .

Hack Hash

问题：给两个长度为 \(n\) 的序列 \(a,b\) . \(q\) 次询问，每次给两个区间 \([l_1,r_1],\,[l_2,r_2]\)，问 \(a_{l_1,\dots,r_1},\,b_{l_2,\dots,r_2}\) 组成的可重集是否相等 .

算法：\(p=998244353\)，取随机映射 \(f:\mathbb Z_n\to\mathbb Z_p\)，判断 \(\mathbb F_p\) 下透过 \(f\) 的区间乘积是否相等 .

想要 Hack 掉这个算法！\(q\) 组询问只要一组爆炸就算对，要求正确率超过 \(80\%\) . 数据范围：\(n+q\le 10^6\) .

感觉也想了一些类似的东西，但是就是没有到达对的地步 . 以下是复读官方题解 .

首先用原根变成 \(m=\varphi(p)\)，取随机映射 \(f:\mathbb Z_n\to \mathbb Z_m\)，在 \(\mathbb F_m\) 下判断区间和是否相等 .

假如用两个长度为 \(k\) 的序列 \(A=\langle a,a,\cdots,a\rangle,\,B=\langle b,b,\cdots,b\rangle\)，那么：

\[\operatorname{Hash}(A)-\operatorname{Hash}(B)=k(f(a)-f(b))\pmod m \]

取 \(k\mid m\)，那么 \(k\mid(\operatorname{Hash}(A)-\operatorname{Hash}(B))\)，这里总共只有 \(\frac km\) 种数，所以随便选 \(a,b\) 的碰撞概率就是 \(\frac km\) .

这么构造：

\[\begin{aligned}&A=\langle1,1,\cdots,1,2,2,\cdots,2,\cdots,c,c,\cdots,c\rangle\\&A=\langle c+1,c+1,\cdots,c+1,c+2,c+2,\cdots,c+2,\cdots,2c,2c,\cdots,2c\rangle\end{aligned} \]

其中每个都重复 \(k\) 遍 . 这样总共可以拼出 \(\frac{c^2(c+1)^2}4\) 组询问，每组询问可以看成独立的一次试验，则正确率：

\[\operatorname{prob}(c)=1-\left(1-\dfrac km\right)^{\frac{c^2(c+1)^2}4} \]

然后要求 \(ck+\frac{c^2(c+1)^2}4\le10^6\) 且 \(k\mid m\) . 可以绘制一下图像（\(c-\operatorname{prob}(c)\)）：

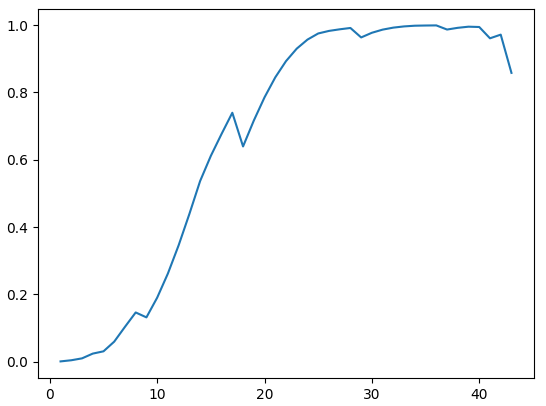
算出来是取 \(k=15232,\,c=36\) 最优，此时正确率 \(\operatorname{prob}(c)>0.9988\) . 可以通过！