小题狂练 (E)

目录

目录

• [省选联考 2020 B 卷] 丁香之路
• [JSOI2019] 精准预测
• [AGC026D] Histogram Coloring
• [AGC049D] Convex Sequence
• [AGC058D] Yet Another ABC String
• [CEOI2014] The Wall
• [ABC217H] Snuketoon
• [POI2010] MOS-Bridges
• [SDOI2016] 墙上的句子
• [ARC175F] Append Same Characters

[省选联考 2020 B 卷] 丁香之路

对于固定起点、终点 \(s,t\)，相当于给一个边集 \(E_0\)，找一个尽可能小的边集 \(E\supseteq E_0\) 使得 \(E\) 对应的子图中存在一条 \(s-t\) 的欧拉路 .

考虑先加一条 \((s,t)\) 转为欧拉回路，然后首先把 \(E\) 的每个点度数补成偶数且连通尽量多的点：考虑每个 \(2\nmid\deg(u)\) 的 \(u\)，然后按顺序两两匹配，对于一组 \((u,v)\)，依次连 \((u,u+1),\cdots,(v-1,v)\) 来使得它们的度数奇偶性翻转 .

操作完之后只需要再连一些边使得每个度数不为 0 的点都连通，这个可以使用最小生成树简单解决 .

时间复杂度 \(\tilde\Theta(n^2+m)\) .

[JSOI2019] 精准预测

类似 2-SAT 地，对每个时刻 \(t\) 上的居民 \(x\) 建立结点 \(\operatorname{alive}(t,x),\operatorname{dead}(t,x)\)，然后刻画出 0 操作和 1 操作还有不能复活的限制之后就是问对于每个 \(\operatorname{alive}(T+1,x)\) 有多少个 \(y\) 使得 \(\operatorname{alive}(T+1,x),\operatorname{alive}(T+1,y)\) 都不能到 \(\operatorname{dead}(T+1,y)\) . 显然只有 \(O(n+m)\) 个点是关键的，那么大力建图后直接 bitset 跑 DAG 可达性就可以了 .

由于这个题比较毒瘤所以需要一系列卡常：

• 时间上：需要使用 DFS 进行 DP，不要写 BFS 的拓扑排序；注意到只有限制中作为 \(x\) 的位置才可能有用，\(y\) 的位置并没有什么用，于是可以把每个 \(y\) 的限制对应的时间改成离它最近的作为 \(x\) 操作数的时间，这个操作大概可以让点数除以二 .
• 空间上：由于开不下全的 bitset 所以需要分段做，令块长为 \(B\) 则每次只记录 \(B\) 个点的可达性，做 \(\frac nB\) 次 .

[AGC026D] Histogram Coloring

先考虑如果矩形是整的那么就考虑每行相当于必须填下一行的 flip，如果下一行全同色则也可以和下一行填一样的 .

那么对于任意棋盘也可以考虑每次填最下面一行，但是此处删掉一行之后序列可能会分裂成若干部分，此处可以递归进入子问题 . 大概是一个笛卡尔树的结构 .

[AGC049D] Convex Sequence

如果 \(a\) 单调增的话就是要求 \(a\) 的差分数组单调增并且它的二阶前缀和等于 \(m\)，那么 Abel 变换拆一下贡献可以得到方案数为 \(\displaystyle p(m)=[x^m]\prod_{k\ge1}\dfrac{1}{1-x^{k(k+1)/2}}\) .

对于原题来说考虑枚举最小值就变成了两个单调增的问题卷起来，相当于要算 \(O(n)\) 个：

\[[x^m]\prod_{k=1}^a\dfrac{1}{1-x^{k(k+1)/2}}\prod_{k=1}^b\dfrac{1}{1-x^{k(k+1)/2}} \]

然而发现本质不同的 \((a,b)\) 对只有 \(O(\sqrt m)\) 种，于是直接动态维护每个位置的系数，只需要每次乘或除一个 \(\frac1{1-x^c}\) .

总时间复杂度 \(O(m\sqrt m)\) 可以通过 . 我们 GF 批是这样的

[AGC058D] Yet Another ABC String

符号化容斥初探， specify 部分贺的讲题课件的，似乎和目前能看见的题解的处理方法都不太一样 .

[CEOI2014] The Wall

首先注意到城墙一定包含到每个村庄的左上角的最短路，可以调整证明：

那么求出最短路树之后就是要求包含所有最短路的最小城墙，把每个点拆成四个方向的接头之后做最短路就可以了：

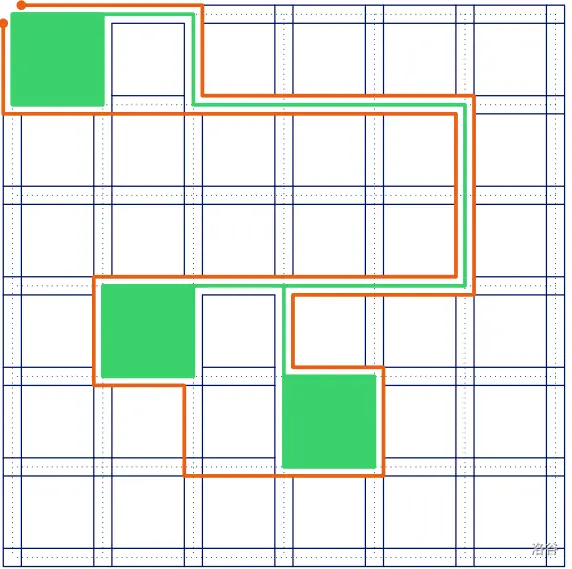
时间复杂度 \(\Theta(\operatorname{SSSP}(nm,nm))\)，可以通过 .

[ABC217H] Snuketoon

Slope Trick 模板 . 后称连续的凸分段线性函数为折线函数 .

首先朴素 DP，\(dp_{i,j}\) 表示时刻 \(t_i\) 位于 \(j\) 的最小代价，则：

\[dp_{i,j}=\min_{|k-j|\le t_i-t_{i-1}}\{dp_{i-1,k}\}+f_{d_i}(x_i,j) \]

由于 \(f\) 是折线函数，转移相当于平移取 min，所以 \(dp\) 也是折线函数 . 然后开两个堆分别维护左右凸壳就行了 .

[POI2010] MOS-Bridges

二分答案后变成求混合图欧拉回路，也就相当于给每条无向边定向后图是欧拉图 .

有向图是欧拉图当且仅当入度和出度相等，首先特判存在 \(u\) 使得 \(2\nmid\deg(u)\) 时无解 .

对于其余情况，先随便定向，然后算出每个点 \(u\) 的入度 \(\operatorname{in}(u)\) 和出度 \(\operatorname{out}(u)\) .

令源点为 \(s\)、汇点为 \(t\)，那么考虑这样建立最大流模型：

• 对于 \(\operatorname{in}(u)>\operatorname{out}(u)\) 的点 \(u\)，连一条 \(s\to u\) 容量为 \(\frac{\operatorname{in}(u)-\operatorname{out}(u)}2\) 的边，表示需要流入这么多流量平衡度数 .
• 对于 \(\operatorname{in}(u)<\operatorname{out}(u)\) 的点 \(u\)，连一条 \(u\to t\) 容量为 \(\frac{\operatorname{out}(u)-\operatorname{in}(u)}2\) 的边，表示需要流出这么多流量平衡度数 .
• 对于原先的一条定向为 \(u\to v\) 的双向边 \(u,v\)，连一条 \(v\to u\) 容量为 \(1\) 的边，表示可以流 \(1\) 翻转这条边的方向 .

然后计算 \(s\to t\) 的最大流即可 . 如果满流说明存在欧拉回路，接下来只需要看每条 \(v\to u\) 的边是否流即可得到每条边的方向，接下来跑有向图欧拉回路即可得到方案 . 时间复杂度 \(O(\operatorname{maxflow}(n,n+m)\log V)\)，可以通过 .

[SDOI2016] 墙上的句子

大概一个二选一模型的套路吧 .

首先把回文的丢掉，然后相当于 \(n+m\) 组字符串上的问题 . 如果 \(x>x^{\sf R}\) 那么令 \(x\gets x^{\sf R}\) 这样每个位置的字典序都小于翻转后的字典序 .

建立最小割模型：源汇点为 \(s,t\)，首先对于每个串都连 \(x\to x^{\sf R}\)，容量为 \(2\) .

对于阅读顺序确定的串，若正串一定出现则连 \(s\to x\)，若反串一定出现则连 \(x^{\sf R}\to t\)，容量均为 \(+\infty\) .

关于阅读顺序不确定的串，考虑到所有串的阅读方向肯定都是一样的，对于每个字符串簇 \(u\) 和其上的字符串 \(x\) 连容量为 \(+\infty\) 的边 \(u\to x\) 和 \(x^{\sf R}\to u\) 来绑定每个字符串即可 .

[ARC175F] Append Same Characters

由于某些原因我先不写证明，直接给出以下结论：

• \(\operatorname{comp}(X,YX)=\operatorname{comp}(X,Y^{\infty})\) .
• \(\operatorname{comp}(XY,YX)=\operatorname{comp}(X^{\infty},Y^{\infty})\) .
• 对于 \(XY\neq YX\)，\(\operatorname{LCP}(XY,YX)=\operatorname{LCP}(X^{\infty},Y^{\infty})\) .

首先相当于给每个字符串后面加一个字符串 \(X\) 并最小化逆序对个数加 \(|X|\) .

考虑什么时候在字符串 \(A<B\) 后面加字符串 \(X\) 会翻转其大小关系 \(AX>BX\)，首先显然有 \(A\) 是 \(B\) 的前缀，那么计算 \(B\) 去掉 \(A\) 之后得到的字符串 \(Y\) 后就相当于 \(X>YX\)，根据结论可以知道相当于 \(X>Y^{\infty}\) .

那么在 Trie 树上找到所有的 \(Y\)，这是 \(O(\sum|s_i|)\) 级别的，然后利用结论 \(\operatorname{comp}(XY,YX)=\operatorname{comp}(X^{\infty},Y^{\infty})\) 给所有 \(Y^{\infty}\) 排序，这样只需要枚举一段前缀被影响，然后计算逆序对和最小的合法 \(|X|\) 即可 .

首先对于逆序对可以直接在 Trie 树上计算有多少对逆序对涉及到某个 \(Y\)，这是简单的 . 对于最小的合法 \(|X|\) 就相当于要计算两个相邻的 \(Y^{\infty}\) 的 LCP，直接用结论就可以了（\(X\) 比所有 \(Y^{\infty}\) 大的情况要单独算一下）.

时间复杂度 \(O(n+\sum|s_i|\log^2n)\)，瓶颈在对 \(Y^{\infty}\) 排序上 . 如果使用 SA 比较就可以去掉一个 log，虽然跑得也没 Hash 快吧 .