2024.11.7 闲话

xrlong 的瑞士军刀 .

歌：素直になれたなら - えいぐふと feat. 歌愛ユキ .

T

目录

• 理论
  • 树的簇分解
  • Top Tree
• 应用
  • 动态 DP
  • 范围修改查询
  • 树分治

理论

树的簇分解

定义树 \(T\) 上的簇 (cluster) 是满足以下条件的三元组 \(C=(V,E,B)\)：

• \(B\subseteq V\) 且 \(|B|\le 2\) .
• \(G(V,E)\) 是 \(T\) 的连通子图 .
• 对于每个 \(u\in V\)，若存在 \(v\notin V\) 且 \((u,v)\in E(T)\)，那么 \(v\in B\)（也就是说 \(V\) 中只有 \(B\) 与外界相邻）.

称 \(B\) 是 \(C\) 的界点 (boundary node)，后记 \(V(C),E(C),B(C)\) 为簇 \(C\) 中的 \(V,E,B\) .

簇有两种运算，compress 和 rake：

• 对于簇 \(C,D\) 满足 \(B(C)\cap B(D)=\{v\}\)，则它们的 compress：
  \[\operatorname{compress}(C,D)=(V(C)\cup V(D),E(C)\cup E(D),(B(C)-\{v\})\cup(B(D)-\{v\})) \]
  只有当结果还是簇时才能运算 .
• 对于簇 \(C,D\) 满足 \(B(C)\cap B(D)=\{x\}\)，则它们的 rake：
  \[\operatorname{rake}(C,D)=(V(C)\cup V(D),E(C)\cup E(D),B(C)) \]
  只有当结果还是簇时才能运算 .

如图：

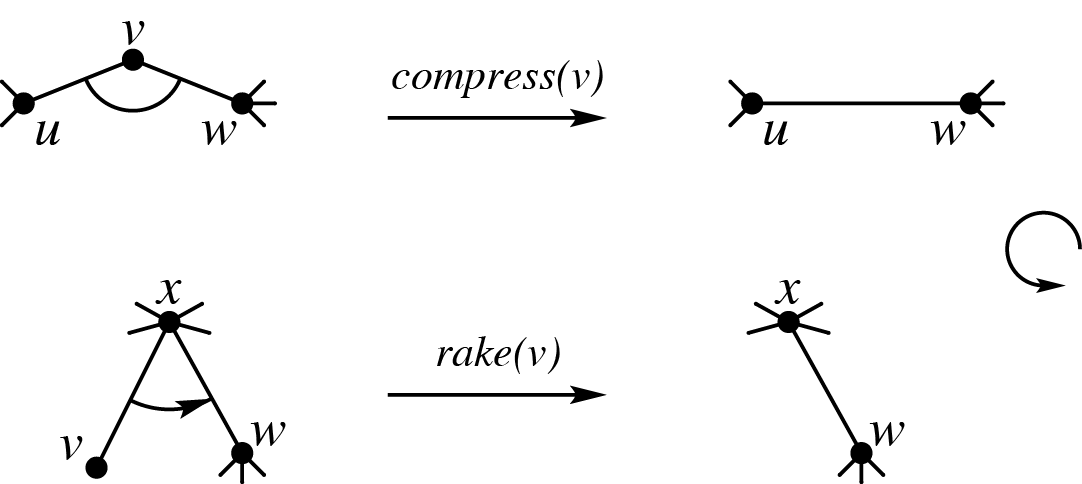
关于 compress 和 rake 如何描述树上信息合并，可以参考 compress, rake, twist 对于广义串并联图上信息合并的描述：广义串并联图方法（这里三种操作分别对应缩 2 度点、删 1 度点、叠合重边）.

Top Tree

容易发现可以从初始每条边孤立每次 compress 或 rake 两个簇得到整棵树构成的簇 .

具体只需要每次选择树上的一个叶子 \(x\)，如果它有兄弟则 rake 过去否则 compress 到父边上即可 .

如图为每个时刻的树及运算过程：

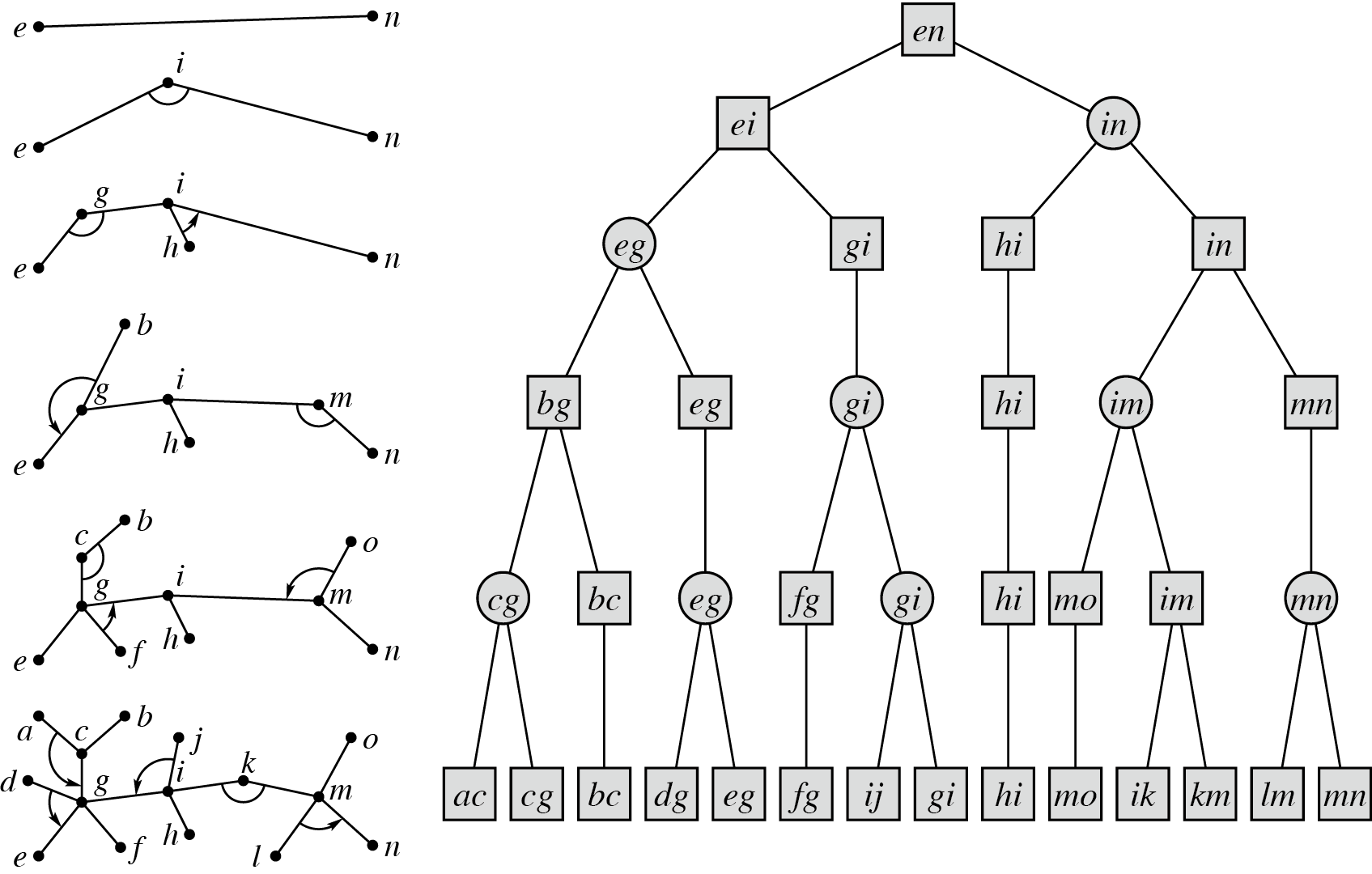
上图方点表示 compress，圆点表示 rake .

称这样的运算过程构成的表达式树为 Top Tree，容易发现 Top Tree 一定是二叉的 .

考虑对于一棵树建立一棵深度浅一点的 Top Tree . 首先轻重链剖分，合并子树的时候先把所有轻儿子 rake 到重儿子上，然后重儿子向上 compress . 关于计算轻儿子 rake 起来的值可以考虑每次按重量（子树大小）均匀分为两部分，然后分别处理后 rake 起来 . 对于重链上每个簇 compress 也用类似的分治做 . 对于分治建出的二叉树，compress 部分建出的树被称作 compress 树，rake 部分建出的树被称作 rake 树 .

可以证明这样建出的 Top Tree 的深度为 \(\Theta(\log n)\) . 具体可以考虑在同一棵树上走两步子树大小至少除以二 .

这个大概就是全局平衡二叉树了 .

一个建树的实现，注意簇上的信息不能算界点要不然不好单点修改：

静态 Top Tree

放一个带修最大权独立集的实现，因为经过一些残忍的事情所以可能并不是那么可读 .

void dfs(int u)
{
	siz[u] = 1;
	for (int v : g[u])
	{
		if (v == fa[u]) continue;
		fa[v] = u; dfs(v); siz[u] += siz[v];
		if (siz[son[u]] < siz[v]) son[u] = v;
	}
}
struct cluster{int u, v, info00, info01, info10, info11;};
cluster rake(cluster a, cluster b)
{
	assert(a.u == b.u);
	return {a.u, b.v, max(a.info00 + b.info00, a.info01 + b.info00 + r[a.v]), max(a.info00 + b.info01, a.info01 + b.info01 + r[a.v]), max(a.info10 + b.info10, a.info11 + b.info10 + r[a.v]), max(a.info10 + b.info11, a.info11 + b.info11 + r[a.v])};
}
cluster compress(cluster a, cluster b)
{
	assert(a.v == b.u);
	return {a.u, b.v, max(a.info00 + b.info00, a.info01 + b.info10 + r[a.v]), max(a.info00 + b.info01, a.info01 + b.info11 + r[a.v]), max(a.info10 + b.info00, a.info11 + b.info10 + r[a.v]), max(a.info10 + b.info01, a.info11 + b.info11 + r[a.v])};
}
struct TopTree
{
	int tfa[N], id[N], top[N], cc;
	struct Node{int ls, rs; cluster v; char type;}tr[N << 1];
	void composite(int& u, vector<pii> v, char T)
	{
		if (v.size() == 1){u = v.front().first; return ;}
		if (!u){u = ++cc; tr[u].type = T;}
		int tot = 0, sum = 0;
		for (pii x : v) tot += x.second;
		vector<pii> side;
		bool c = true;
		for (int i=0; i<v.size(); i++)
		{
			auto [x, s] = v[i]; sum += s; side.emplace_back(x, s);
			if (c && ((sum * 2 > tot) || (i == v.size() - 2))){composite(tr[u].ls, side, T); side.clear(); c = false;}
		}
		composite(tr[u].rs, side, T);
		if (T == 'R') tr[u].v = rake(tr[tr[u].ls].v, tr[tr[u].rs].v);
		if (T == 'C') tr[u].v = compress(tr[tr[u].ls].v, tr[tr[u].rs].v);
		tfa[tr[u].ls] = tfa[tr[u].rs] = u;
	}
	void dfs(int x)
	{
		if (!id[x]) top[x] = id[x] = ++cc;
		int u = id[x];
		if (fa[x] && (g[x].size() == 1)){tr[u].type = 'P'; tr[u].v = {fa[x], x, 0, 0, 0, -INF}; return ;} // leaf
		for (int v : g[x])
			if (v != fa[x]) dfs(v);
		vector<pii> lson;
		for (int v : g[x])
			if ((v != fa[x]) && (v != son[x])) lson.emplace_back(top[v], siz[v]);
		if (lson.empty()) tr[u].v = {x, son[x], 0, 0, 0, -INF};
		else
		{
			tr[u].type = 'R'; tr[u].rs = ++cc; tr[tr[u].rs].v = {x, son[x], 0, 0, 0, -INF};
			composite(tr[u].ls, lson, 'R'); tr[u].v = rake(tr[tr[u].ls].v, tr[tr[u].rs].v);
			tfa[tr[u].ls] = tfa[tr[u].rs] = u;
		}
		if ((x == 1) || (son[fa[x]] != x))
		{
			vector<pii> chain; int t = x;
			if (fa[x]){chain.emplace_back(++cc, 0); tr[cc].type = 'P'; tr[cc].v = {fa[x], x, 0, 0, 0, -INF}; }
			while (son[t]){chain.emplace_back(top[t], siz[t] - siz[son[t]]); t = son[t];}
			int R = 0; composite(R, chain, 'C'); tfa[top[t]] = top[x] = u = R;
		}
	}
	void build(){dfs(1);}
	inline void change(int x, int c)
	{
		int u = id[x]; r[x] = c;
		while (u)
		{
			if (tr[u].type == 'R') tr[u].v = rake(tr[tr[u].ls].v, tr[tr[u].rs].v);
			if (tr[u].type == 'C') tr[u].v = compress(tr[tr[u].ls].v, tr[tr[u].rs].v);
			u = tfa[u];
		}
	}
	int query(){auto x = tr[top[1]].v; return max({x.info00, x.info10 + r[x.u], x.info01 + r[x.v], x.info11 + r[x.u] + r[x.v]});}
}T;

应用

动态 DP

NOIP2018 保卫王国

直接看成单点修改最大权独立集 . 每个簇上维护 \(f_{0/1,0/1}\) 记录钦定两界点的状态的最大独立集，两种信息合并都可以平凡维护 . 一般是界点的贡献都不算，这里也可以写成贡献算下界点不算上界点 .

单点修改的时候只需要找到 Top Tree 上对应的结点然后把它的根链重新 pushup 一遍即可 .

Dynamic Diameter

维护直径就是合并的时候类似最大子段和那样讨论是否经过两个簇的交点就可以了 .

范围修改查询

这里分别讨论三种树上的范围：子树、链、邻域 . 问题本质上是要找出若干簇使得它们的并是某种范围 .

子树：由于子树本身就是一个簇所以只需要在 Top Tree 上 DFS 找出所有子树内的极大簇然后合并即可 .

链：首先找出 \(u,v\) 对应 Top Tree 上结点的 LCA \(l\)，容易发现 \(l\) 是极小的包含 \(u,v\) 的簇 . 取 \(l\) 两个儿子的交点 \(x\)，然后可以将问题划分为 \((u,x),(x,v)\) 两条链 . 这样的两条链都是形如某个结点到某个界点的，那么可以每次讨论路径在簇上哪边的儿子递归下去做 .

邻域：树上邻域数点 . 以后再看吧魔怔了吧 . 等着 gtm 写

树分治

其实好像就是直接做 . 摆烂不写了

图