小题狂练 (D)

目录

目录

• CF461E Appleman and a Game
• CF925C Big Secret
• CF444E DZY Loves Planting
• CF446E DZY Loves Bridges
• CF763D Timofey and a flat tree
• CF1181E2 A Story of One Country (Hard)
• CF788D Finding lines
• CF1392H ZS Shuffles Cards
• ARC126E Infinite Operations
• CF708E Student's Camp
• SPOJ MUZIDA - Muzidabutur
• P8151 彼岸 | To See the Next Part of the Dream
• UOJ#810 比特迷宫
• CF1685C Bring Balance
• CF1667C Half Queen Cover
• ARC172D Distance Ranking
• CF883D Packmen Strike Back
• CodeFestival2017qualC Three Gluttons
• CF1179E Alesya and Discrete Math
• ARC130E Increasing Minimum
• BJOI2014 想法
• S8PC5F Lunch Menu
• ARC128F Game against Robot
• CF1842D Tenzing and His Animal Friends

CF461E Appleman and a Game

首先如果 \(s\) 给定判断能否匹配就是在后缀树上贪心，因为有单调性所以可以考虑处理出操作若干次能得到的最长的 \(s\) 的长度 . 只需要对于每个 \((c_1,c_2)\) 处理出 \(c_1\) 开头且后面加一个 \(c_2\) 就不是子串的最短子串长度 \(w_{c_1,c_2}\)，然后求答案时合并若干个这样的结构，转移是 \((\min,+)\) 矩阵乘法 . 此处可以倍增进行这个过程 .

这里并不需要真的建出完整的后缀树，注意到每个子串的长度大于 \(\log_{|\Sigma|}|t|\) 时一定不优，所以可以在 Trie 上依次插入每个后缀并在 \(\log_{|\Sigma|}|t|\) 深度处截断 .

CF925C Big Secret

注意到一个位置合法当且仅当它的最高位在前面为 1 的个数是偶数个，那么按最高位从小到大排序贪心插入即可 .

时间复杂度 \(\tilde O(n)\) .

CF444E DZY Loves Planting

考虑一下怎么判断 \(f(P)\ge x\)，把边权 \(\ge x\) 的边删掉形成若干连通块，每个点只能和与自己不在同一个连通块内的点匹配 . 那么只需要判断每个连通块内的 \(x_i\) 之和是否小于其它连通块的 \(x_i\) 之和即可 .

这里注意到 \(f(P)\) 肯定是某个边权，所以只需要按顺序加入每条边然后并查集维护连通块即可维护 .

时间复杂度 \(O(n\alpha(n))\) .

CF446E DZY Loves Bridges

相当于矩阵 \(B_{i,j}=\operatorname{lowbit}(i-j)=\operatorname{lowbit}(i\oplus j)\) 其中 \(\operatorname{lowbit}(0)= 0\)，给列向量 \(\bm v\) 求 \(B^t\bm v\) .

注意到令大小为 \(2^m\) 的 lowbit 矩阵为 \(B_m\) 则有：

\[B_m=\begin{bmatrix}B_m&B_m+(2^m-1)I\\B_m+(2^m-1)I&B_m\end{bmatrix} \]

二阶矩阵的幂对角化一下就能求了（此处矩阵对称一定可以对角化），那么回代到矩阵乘法的式子里每次可以让问题规模减小一半，这样分治即可在 \(O(2^m+m\log t)\) 的时间复杂度内完成问题 .

CF763D Timofey and a flat tree

直接维护树 Hash，每次根移动一步只会改 2 个结点的 Hash 值 .

CF1181E2 A Story of One Country (Hard)

矩形划分过程是一个分治的模式：每次找到任意一条水平或垂直的不过任何关键矩形的直线然后分割 .

考虑直接模拟分治流程，此处划分的时候用一下启发式：从四个方向同时往对面扫，这样一个分割点一定是由离它最近的那个边界扫到，这样就可以保证每次只需要处理分割点两侧较小的那一部分 .

时间复杂度 \(O(n\log n)\) 或 \(O(n\log^2n)\)，取决于实现方式 .

CF788D Finding lines

每条直线都和 \(y=x\) 相交，考虑在 \(y=x\) 上分治：对于区间 \([l,r]\) 中点 \(x\) 查询 \((x,x)\) 的答案 \(k\)，并分治进入 \([l,x-\min\{k,1\}],[x+\max\{k,1\},r]\) .

查询之后取一个不在任何线段上的点 \((p,p)\)，对于每个线段上的点 \((x,x)\)，只需要查询 \((x,p),(p,x)\) 即可知道 \((x,x)\) 上有没有垂直或者水平的直线 .

可以简单分析到交互次数不大于 \(7(n+m)\) 次，实际上界较松 .

CF1392H ZS Shuffles Cards

对于每张牌 \(x\) 记 \(P(x)\) 表示它后面第一张 JOKER 的是第几张抽出的 JOKER . 那么设抽出一次 JOKER 的期望步数是 \(T\)，答案就是 \(T\cdot\mathbb E(\max P(x))\) .

使用 min-max 容斥转为对于每个子集算 \(\mathbb E(\min P(x))\)，此处对一轮以 JOKER 结尾的抽牌做 SEQ 构造就可以了 .

ARC126E Infinite Operations

注意到答案为 \(\frac12\sum|a_i-a_j|\)，具体可以设势能函数为 \(\sum|a_i-a_j|\) 考虑每次操作对势能的影响来证明 .

从而值域线段树维护即可，时间复杂度 \(O(n\log V)\) .

CF708E Student's Camp

直接做 .

SPOJ MUZIDA - Muzidabutur

令 \(C\) 是字符集大小，字符编号从 \(0\) 开始 .

根据经典 DP 可知令 \(M_i\) 是满足 \(M_{s_i,s_i}=0,\,M_{s_i,C}=-1,\,M_{C,s_i}=1,\,M_{C,C}=2\)，其它位置的 \(M_{i,j}=[i=j]\) 的矩阵，\(\bm v=[0,0,\cdots,1]\)，则答案就是 \((\bm v\prod_{i\in[l,r]}M_i)_C\) . \(M\) 和 \(M^{-1}\) 大概是个下面这种样子：

\[M=\begin{bmatrix}1&&&&&&\\&1&&&&&\\&&\ddots&&&&\\&&&0&&&1\\&&&&\ddots\\&&&&&1\\&&&-1&&&2\end{bmatrix}\qquad\qquad M^{-1}=\begin{bmatrix}1&&&&&&\\&1&&&&&\\&&\ddots&&&&\\&&&2&&&-1\\&&&&\ddots\\&&&&&1\\&&&1&&&2\end{bmatrix} \]

可以改成算 \((\bm v\overset{\leftarrow}\prod_{i<l}M_i^{-1}\overset{\rightarrow}\prod_{i\le r}M_i)_C\)，其中箭头标识乘法方向 . 考虑预处理每个 \(A_n=\overset{\leftarrow}\prod_{i\le n}M_i^{-1}\) 和 \(B_n=\overset{\rightarrow}\prod_{i\le n}M_i\)，注意到一个矩阵乘 \(M\) 或 \(M^{-1}\) 只会带来 \(O(C)\) 项的修改，那么直接做就是 \(O(nC)\) 预处理 .

此处 \((\bm vA_{l-1}B_r)_C=\sum_iA_{l-1,C,i}B_{r,i,C}\)，那么每个 \(A_i\) 只需要存第 \(C\) 行的、\(B_i\) 只需要存第 \(C\) 列的值，这样就是 \(O(nC)\) 的空间了 . 查询的时候 \(O(C)\) 计算上一行的式子就可以了 .

时间复杂度 \(O((n+q)C)\) . 回顾一下，\(C\) 是字符集大小 .

P8151 彼岸 | To See the Next Part of the Dream

首先这个变换就是把下标乘 2，那么可以导出答案的表达式：

\[\begin{aligned}f(n)&=\sum_{i=0}^{n-1}\sum_{t=1}^{2^n}[2^it\equiv t\pmod{2^n+1}]\\&=\sum_{i=0}^{n-1}\sum_{t=1}^{2^n}\left[\dfrac{2^n+1}{\gcd(2^n+1,2^i-1)}\mathop{\Big\vert}t\right]\end{aligned} \]

注意到：

\[\gcd(2^n+1,2^k-1)=\gcd\left(\dfrac{2^{2n}-1}{2^n-1},2^k-1\right)=\dfrac{\gcd(2^{2n-1},2^k-1)}{\gcd(2^n-1,2^k-1)}=\dfrac{2^{\gcd(2n,k)}-1}{{2^{\gcd(n,k)}-1}} \]

通过讨论可得长度为 \(l\) 的因数的置换环的个数 \(t_l=\left[2\mid\frac{l}{\gcd(n,l)}\right]2^{\gcd(n,l)}\) .

然而发现此时走 \(n\) 步一定是恰好走一半，那么令 \(g(n)\) 是走完的答案则 \(f(n)=\frac{g(n)+2^n}2\)，于是可以考虑计算 \(\sum g(i)\) 然后简单修正到 \(\sum f(i)\) . 对 \(t_l\) 用莫反后进行一些简单的推导可以得到：

\[\sum_{i=1}^ng(i)=\sum_{i=1}^n2^iS^{{\star}}\left(\left\lfloor\dfrac nd\right\rfloor\right)\text{ where }S^{\star}(n)=\sum_{i=1}^n(i\bmod 2)\varphi(i) \]

如果令 \(\displaystyle S(n)=\sum_{i=1}^n\varphi(i)\) 则可以归纳证明 \(\displaystyle S^\star(n)=S(n)-\sum_{i\ge1}S\left(\left\lfloor\dfrac n{2^i}\right\rfloor\right)\) .

杜教筛求出 \(S\) 的块筛之后就可以 \(O(\log n)\) 求 \(S^\star\) 了，总时间复杂度 \(O(n^{2/3})\) .

UOJ#810 比特迷宫

还是乱搞吧 . 首先随机操作让多项式变随机，然后每次选择操作后 1 最多的位置操作 .

CF1685C Bring Balance

首先转成格路，那么相当于每次可以把一段 Dyck 路沿中点中心对称，要求操作后路径没有任何一部分在 \(x\) 轴下方 .

首先 2 步之内必有解，因为可以找到最高的位置 \(p\) 然后操作 \([1,p],(p,2n]\)，合法性显然 . 那么只需要判断能否 1 步完成，首先找到最左边和最右边的在 \(x\) 轴下方的位置 \(l,r\)，那么操作的区间 \([L,R]\supseteq[l,r]\)，显然只需要考虑高的位置会不会被翻下来那么需要中点尽可能高，于是找到 \(l\) 左边和 \(r\) 右边最大的位置当做 \(L,R\) 检验即可 .

时间复杂度单次 \(\Theta(n)\) .

CF1667C Half Queen Cover

首先 \(3\nmid n\) 大概就是在 UOJ 图标的颜色边界上放棋子，这里两边的棋子数分别取 \(\lfloor\frac n3\rfloor,\lfloor\frac{n+2}3\rfloor\) .

对于 \(3\mid n\) 首先构造出 \((n-1)\times(n-1)\) 的答案然后在右下角放一个子即可 .

容易证明上述构造取到理论下界 .

ARC172D Distance Ranking

首先如果所有距离全部相等可以构造 \((1,0,\cdots,0),(0,1,\cdots,0),\cdots,(0,0,\cdots,1)\)，考虑在其上调整得到答案 .

考虑如果给某个 \(p_{i,j}\) 加一个扰动 \(\varepsilon\)，则 \(d(p_i,p_j)^2\) 减小 \(2\varepsilon-\varepsilon^2\)，其它到 \(p_i,p_j\) 的距离的平方减小 \(\varepsilon^2\) 级别 . 这样就让 \(d(p_i,p_j)\) 成为最小值了 .

那么可以取一列同阶无穷小 \(\varepsilon_1<\varepsilon_2<\cdots\) 按排名依次扰动每个距离，由于此处 \(\varepsilon^2\) 低阶于 \(\varepsilon\) 所以可以忽略其影响 .

实现上可以先取 \(p_{i,i}=10^8\) 然后其它位置的 \((i,j)\) 取递减排序后它的排名，可以通过计算得到此处 \(\varepsilon^2\) 的误差并不会影响排名 .

CF883D Packmen Strike Back

首先如果只有 1 个 P 那么平凡，否则一定可以覆盖所有的 * .

二分答案后令 \(dp_i\) 表示前 \(i\) 个 * 能覆盖的最长的一个 * 前缀有多长，转移的时候讨论三种情况：

• 第 \(i\) 个 P 朝左 .
• 第 \(i\) 个 P 朝右 .
• 第 \(i\) 个 P 朝左，第 \(i-1\) 个 P 朝右 .

时间复杂度 \(O(n\log n)\) .

CodeFestival2017qualC Three Gluttons

首先倒着考虑每一位三个人都选的什么，对于最后一位可以发现如果 A, B, C 分别选 \(x,y,z\) 那么对于 C 序列必须有 \(z\) 在 \(x,y\) 前面 . 再走一步的话需要限制这一次选的要在下一次选的前面，别的就不用做限制了 . 总之可以对于一种选择的方案共有 \(\prod(3i-1)(3i-2)\) 种满足条件的序列 .

那么就转为计数选择方案，这里令 \(dp_{t,i,j}\) 表示考虑到第 \(t\) 次选择，A, B 分别选了 \(i,j\) 的方案数即可简单转移 .

这里需要前缀和优化一下，时间复杂度 \(\Theta(n^3)\) .

CF1179E Alesya and Discrete Math

分治：每次找到一排位置 \(\{x\}\) 使得 \(f_i(x_i)=\frac L2\)，把 \(x\) 排序后前面一半和后面一半可以划分为子问题 .

关于如何找到这样的位置：根据单调性分到前面的 \(f\) 肯定满足 \(f(x_{n/2})\ge\frac L2\)，后面的 \(f\) 肯定满足 \(f(x_{n/2})\le\frac L2\) . 那么相当于要找到一个中位函数 \(f^{\star}\) 和它上面值等于 \(\frac L2\) 的位置 \(x^{\star}\)，然后按 \(f_i(x^{\star})\) 和 \(f^{\star}(x^{\star})\) 的大小关系划分左右 .

可以考虑这样一个算法（类似 nth_element 的快速选择）：每次随机一个函数 \(f\) 作为 \(f^{\star}\) 然后按上面的方法划分，这样中位函数一定在多的一边，可以单侧递归进去 .

复杂度分析：令 \(b=\log_2n\) 则时间复杂度为 \(O(\log V\sum_{i=1}^n(n-i)2^i)=O(n\log V)\) . 总时间复杂度为 \(O(n(\log n+\log V))\) .

ARC130E Increasing Minimum

考虑按 \(A_{I_i}\) 的值划分序列 \(I_i\)，那么每一段的每个数都不相同且每一段都是后一段的子集 .

容易发现此时直接贪心选就可以了，最后一段需要特殊处理 . 时间复杂度 \(\Theta(n+k)\) .

BJOI2014 想法

2024.10.24 闲话，不多解释（

S8PC5F Lunch Menu

从小到大考虑 \(a\) 去掉 max 的限制，DP 记当前区间左右端点、考虑到的 \(a\) 的位置和当前操作次数即可 .

时间复杂度 \(\Theta(n^5)\) .

ARC128F Game against Robot

首先把 \(n\) 除以 2 . 按 \(p\) 排序后考虑一种选择方案中 Robot 选择的位置只需要满足前 \(2i\) 个选择至少 \(i\) 个，那么 Snuke 选择的方案就是后 \(2i\) 个选至少 \(i\) 个 . 从而如果 \(p\) 固定计算权值就是从后往前每次加入两个数然后取出最大值，权值即为取出的数之和 .

首先由对称性可以翻转到从前往后，根据上述推导可知选择顺序之与 \(a\) 的大小关系相关，所以只需要计算 \(f_i\) 表示第 \(i\) 大的数被选的次数，这里可以先容斥到前 \(i\) 大的数的次数和 .

考虑把前 \(i\) 大的数记为 1、其它位置记 0，每次加两个数考虑队列里 1 的个数可以双射双色 Motzkin 路：

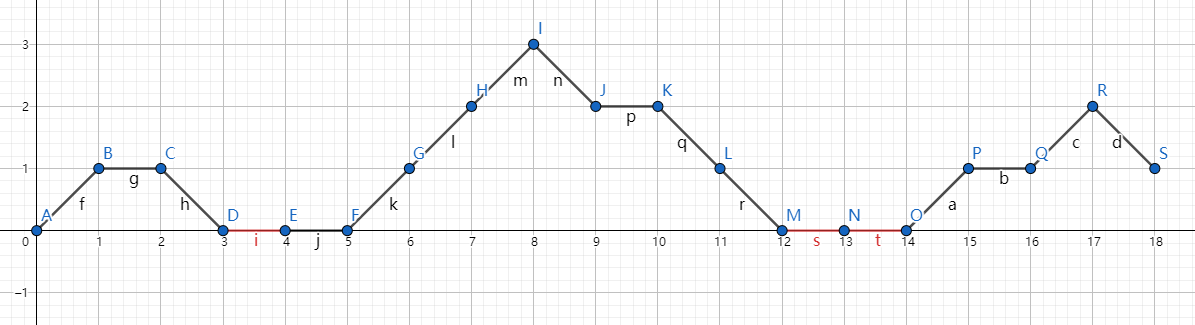
问题就是计数所有路中红边个数之和 . 可以直接去掉这个限制然后把终点平移下去：

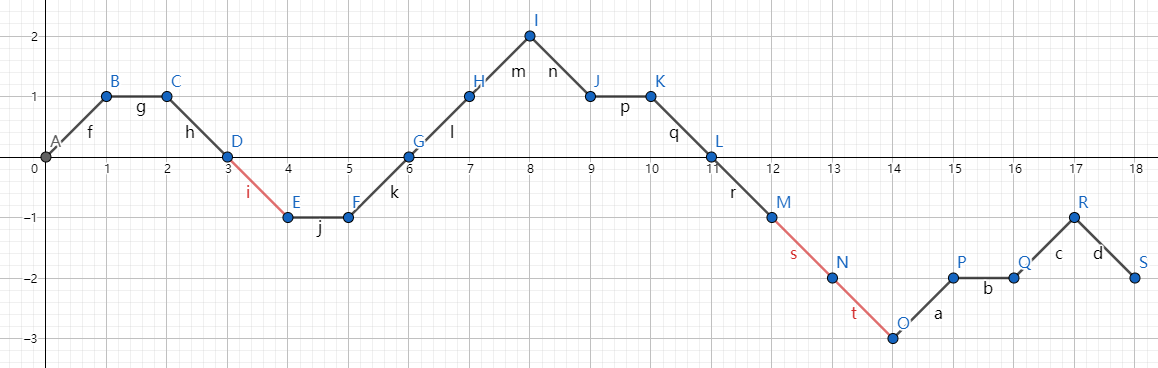
然后这里红线个数就相当于最小值的位置 . 那么枚举最小值就是要数不经过某个横线下方的双色 Motzkin 路数量 . 后面就比较经典了：限制路径位置就是 Catalan 数的反射容斥，双色 Motzkin 路计数可以双射 Dyck 路算（这个 Catalan Addendum 有）.

总之最后化简出来就是除排序外 \(\Theta(n)\) 的，可以通过 .

CF1842D Tenzing and His Animal Friends

Solution 1

显然可以最短路，然后就 1log 了。

具体懒得写，相信大家都会。

Solution 2

Floyd 用脚维护，不需要任何脑子。

我写了。

Solution 3

邓老师调整法脚做了。

会不会t我不知道，我没写