2024.2.2 闲话

才发现失去闲话之后很多想要说的没有地方说了，不过闲话最好还是有一点学术内容的吧。

怎么能让学术限制我的思维？不行，我要破壁！快用 PIA！（？

Yesterday Once More.

歌：こころちゃん - 一二三 feat. 音街ウナ .

似乎年前集训结束了啊。也真的是要过年了。

STAOI 的比赛顺利结束了，有了 UU 确实靠谱多了。

听说最近的月赛审核队列非常长啊。

重拾以前水闲话的技巧，放个题解吧：

保险丝

给一棵 $n$ 个点的有根树，根是 $1$ 号结点。

定义两个点集 $S_1,S_2$ 的距离为从两个集合分别选出一个点，能得到两点间距离的最小值，即 $\displaystyle\operatorname{dist}(S_1,S_2)=\min_{\substack{u\in S_1\\v\in S_2}}\operatorname{dist}(u,v)$，其中 $\operatorname{dist}(u,v)$ 是点 $u,v$ 间的距离。

定义 $\operatorname{path}(u,v)$ 是 $u$ 到 $v$ 的简单路径上的所有点组成的集合，$\mathcal L$ 是所有叶子组成的集合。

对于固定正整数 $u$，定义满足如下条件的结点 $v$ 构成 $u$ 的半邻域 $\mathring U(u)$：

• $v$ 在 $u$ 子树内；
• $\operatorname{dist}(u,v)\le\operatorname{dist}(\operatorname{path}(1,v),\mathcal L)$。

进而定义：

$$f(x)=\sum_{u\in\mathring U(x)}\prod_{\substack{v\in\operatorname{subtree}(u)\\v\in\mathring U(x)}}F_{\deg v}$$

其中 $\operatorname{subtree}(u)$ 是 $u$ 子树中所有点组成的集合，$\deg u$ 是 $u$ 的度数，$F$ 是 Fibonacci 数列：

$$F_n=\begin{cases}1&n\le 2\\F_{n-1}+F_{n-2}&n\ge 3\end{cases}$$

你需要求出 $f(1),f(2),\cdots,f(n)$ 的值，为减少输出量，你只需要输出它们模 $994007158$ 后的异或和，即 $\bigoplus_{x=1}^n(f(x)\bmod 994007158)$ 即可。
$2\le n,q\le 10^6$。

虽然被各种各样的奇怪方法过了，不过有很多正面评价还是很开心的（

（题目名字是 APJ 起的，和我没关系）

这个提示应该比较明显了，考虑到 $F_2=1$ 所以把树 leafy 化处理，也就是只在 $\deg>2$ 的位置计算贡献。

具体地，对于每个点 $u$，若 $\deg u>2$ 则称其为枢纽点，否则为普通点。

在计算 $f(u)$ 时，令点 $v$ 的贡献是 $\displaystyle \prod_{w\in\operatorname{subtree}(v)\land w\in\mathring U(u)}F_{\deg w}$ 即可将问题转为计算半邻域内所有点的贡献和。

考虑找到 $u$ 半邻域内的所有枢纽点，然后分别计算贡献。结构大体如下：

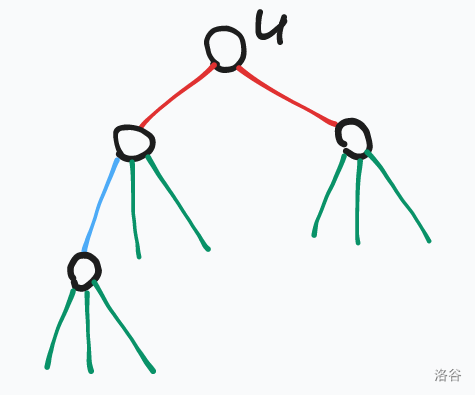
这里只显式画出枢纽点和 $u$，其它普通点省略不画。贡献分为三种：

• 红色边：最上层枢纽点到 $u$ 之间点的贡献。
• 蓝色边：中层枢纽点到上层枢纽点之间点的贡献。
• 绿色边：最下层枢纽点下方普通点的贡献。

红色和蓝色边的贡献可以直接对枢纽点建虚树，然后 DFS 一遍求出每个枢纽点的贡献，这样就可以简单统计所有贡献了。

对于绿色边，因为 $F_2=1$ 所以所有绿色边部分的贡献都是 $1$，即相当于数有多少绿色边位置的点。考虑差分转为数半邻域点数和数半邻域删掉绿色边部分的点数，后者可以用和上面类似的方法求解，对于前者，考察半邻域的结构：记 $k_u=\operatorname{dist}(\operatorname{path}(1,u),\mathcal L)$（容易线性处理），那么 $v\in\mathring U(u)$ 当且仅当 $\operatorname{dist}(u,v)\le k_v$ 也就是 $\operatorname{dep}(v)-\operatorname{dep(u)}\le k_v$。整理可得 $\operatorname{dep}(v)-k_v\le\operatorname{dep}(u)$。加上子树的限制即为二维数点，扫描线即可。

时间复杂度分析：

扫描线部分是单 log 的没有问题，关键在于分析枚举枢纽点的复杂度。

断言：如果 $v$ 是 $u$ 半邻域内的枢纽点，则点对 $(u,v)$ 只有 $O(n\log n)$ 对。

证明：考虑肯定是满二叉树的结构点对数最多，假设树高为 $d$。枚举 $v$ 算有多少个 $u$ 满足条件，这里因为 $u$ 必须是 $v$ 的祖先所以至多有 $d$ 个，从而点对数有上界 $d\cdot 2^d$。

因为 $n=2^d$ 所以可以导出点对的数量是 $O(n\log n)$ 级别的。

（进而可以发现这里实现的一个小细节是找 $u$ 半邻域内的所有枢纽点 $v$ 时，要枚举 $v$ 然后爬树找 $u$，这样可以保证每一步都产生贡献，不会有冗余的枚举）

那么总时间复杂度就是 $O(n\log n)$ 的（实际实现的时候如果建虚树带 log 那么就是双 log 复杂度），可以通过。

Code

const int N = 1e6 + 233, P = 994007158;
int n, deg[N], f[N];
inline void initF(int n)
{
	f[1] = 1;
	for (int i=2; i<=n; i++) f[i] = (f[i-1] + f[i-2]) % P;
}
vector<int> g[N];
inline void addedge(int u, int v){g[u].emplace_back(v); ++deg[u];}
inline void ade(int u, int v){addedge(u, v); addedge(v, u);}
int fa[N], siz[N], dep[N], son[N], top[N], minl[N], rnk[N], dfn[N], cc;
void dfs1(int u)
{
	rnk[u] = ++cc; dfn[cc] = u; siz[u] = 1;
	minl[u] = INT_MAX;
	for (int v : g[u])
	{
		if (v == fa[u]) continue;
		dep[v] = dep[u] + 1; fa[v] = u;
		dfs1(v);
		chkmin(minl[u], minl[v] + 1); siz[u] += siz[v];
		if (!son[u] || (siz[v] > siz[son[u]])) son[u] = v;
	}
	if (minl[u] == INT_MAX) minl[u] = 0;
}
void dfs2(int u, int t)
{
	top[u] = t;
	if (!son[u]) return ;
	dfs2(son[u], t);
	for (auto v : g[u])
		if ((v != son[u]) && (v != fa[u])) dfs2(v, v);
}
int lca(int u, int v)
{
	while (top[u] != top[v])
	{
		if (dep[top[u]] > dep[top[v]]) u = fa[top[u]];
		else v = fa[top[v]];
	}
	return dep[u] > dep[v] ? v : u;
}
vector<int> domi[N];
inline void findu(int v)
{
	int u = v;
	while (u > 0)
	{
		if (dep[v] - dep[u] > minl[v]) break;
		domi[u].emplace_back(v); u = fa[u];
	}
}
struct SimpleGraph
{
	vector<int> g[N];
	inline void addedge(int u, int v){g[u].emplace_back(v);}
	vector<int> operator[](const int& id) const {return g[id];}
	vector<int>& operator[](const int& id){return g[id];}
}G;
int ans1[N], ans2[N], val[N], faG[N];
void dfs3(int u)
{
	val[u] = f[deg[u]];
	for (int v : G[u]) dfs3(v), val[u] = 1ll * val[u] * val[v] % P;
}
inline void solve(int u)
{
	if (deg[u] <= 2) domi[u].emplace_back(u);
	stable_sort(domi[u].begin(), domi[u].end(), [&](int u, int v){return rnk[u] < rnk[v];});
	int len = domi[u].size();
	unordered_set<int> S;
	for (int i=1; i<len; i++){int l = lca(domi[u][i-1], domi[u][i]); S.insert(l); G.addedge(l, domi[u][i]); faG[domi[u][i]] = l;}
	faG[u] = u;	dfs3(u);
	for (int i=0; i<len; i++) (ans1[u] += 1ll * val[domi[u][i]] * (dep[domi[u][i]] - dep[faG[domi[u][i]]]) % P) %= P;
	for (int i=0; i<len; i++) (ans2[u] += (dep[domi[u][i]] - dep[faG[domi[u][i]]]) % P) %= P;
	(ans1[u] += val[u]) %= P; (ans2[u] += 1) %= P;
	for (int x : S) G[x].clear();
}
struct FenwickTree
{
	int a[N];
	inline void add(int x, int v){for (; x<=n; x+=x&-x) (a[x] += v) %= P;}
	inline int query(int x){int ans = 0; for (; x; x&=x-1) (ans += a[x]) %= P; return ans;}
	inline int query(int l, int r){return (query(r) - query(l-1)) % P;}
}T;
vector<int> pnt[N], qry[N];
int main()
{
	scanf("%d", &n); initF(n);
	for (int i=2, u; i<=n; i++){scanf("%d", &u); ade(u, i);}
	dfs1(1); dfs2(1, 1);
	for (int i=2; i<=n; i++) chkmin(minl[dfn[i]], minl[fa[dfn[i]]]);
	for (int i=1; i<=n; i++)
		if (deg[i] > 2) findu(i);
	for (int i=1; i<=n; i++) solve(i);
	for (int i=1; i<=n; i++) qry[dep[i]].emplace_back(i);
	for (int i=1; i<=n; i++)
		if (dep[i]-minl[i] < 0) T.add(rnk[i], 1);
		else pnt[dep[i]-minl[i]].emplace_back(i);
	int res = 0;
	for (int i=0; i<n; i++)
	{
		for (int u : pnt[i]) T.add(rnk[u], 1);
		for (int u : qry[i]) res ^= (((ans1[u] - ans2[u]) % P + T.query(rnk[u], rnk[u]+siz[u]-1)) % P + P) % P;
	}
	cout << res << endl;
	return 0;
}

分割线一号。
分割线二号。
分割线三号。

图片