2024.1.9 闲话

歌：plusar - satie .

好像 HS_xh 那个结论比较平凡啊 .

点击即送

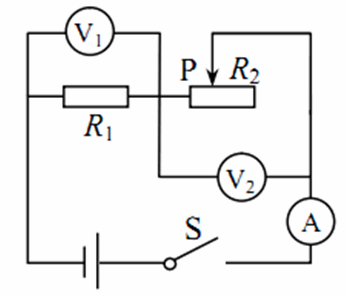
如图（标记不一样），电源电压 $U$ 恒定，定值电阻 $R_0$ 和滑动变阻器并联，证明：

1. 滑动变阻器电功率最大值 $P_{\max}=\dfrac U{4R_0}$ .
2. 滑动划片，得到滑动变阻器阻值为 $R_1,R_2$，其功率分别为 $P_1,P_2$，则 $P_1=P_2\iff R_1R_2=R_0^2$ .

证明：

第一问就直接做，设滑动变阻器阻值为 $R$：

$$\begin{aligned}P_{\max}&=I^2R\\&=\left(U\cdot\dfrac{R}{R_0+R}\cdot\dfrac1R\right)^2\cdot R\\&=\dfrac{U^2R}{(R_0+R)^2}\\&=\dfrac{U^2}{R+\frac{R_0^2}R+2R_0}\\&\le\dfrac{U^2}{2R_0+2R_0}&\text{(AM-GM 不等式)}\\&=\dfrac{U^2}{4R_0}\end{aligned}$$

最后验证一下 $R=R_0$ 取到等号就可以了 .

第二问直接继承上一问的结论可知 $P_1=P_2$ 就相当于：

$$R_1+\dfrac{R_0^2}{R_1}=R_2+\dfrac{R_0^2}{R_2}$$

化简即得 .

偶然间看到 Wikipedia 的页面，终于知道怎么 OGF 和 DGF 转了（

Wikipedia 说：

$$\sum_{n\ge0}\dfrac{f_n}{(n+1)^s}z^n=\dfrac{(-1)^{s-1}}{(s-1)!}\int_0^1\log^{s-1}(t)F(tz)\mathrm dt$$

这也算一种 DGF 转 OGF 了吧，其中 $F(z)$ 是 $\{f\}$ 的 OGF .

但是有一种更正常的转法，经过查阅若干资料之后整合如下 .

（听说已经 well-known 了：

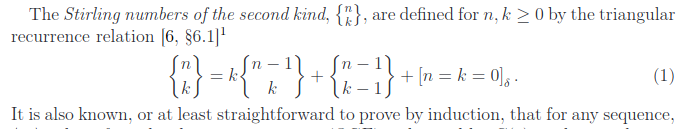
upd. 好像挂错图了，算了不理了 .
）

第二类 Stirling 数：

$${n\brace m}=\dfrac1{m!}\sum_{k=1}^m\dbinom mk(-1)^{m-k}k^n$$

gnilritS 类二第数

$${n+2\brace m}_*=\dfrac1{m!}\sum_{k=1}^m\dbinom mk\dfrac{(-1)^{m-k}}{k^n}$$

可以得到递推：

$${n\brace m}_*=-\dfrac1m{n\brace m-1}_*+\dfrac1m{n-1\brace m}_*+[k=j=1]$$

（注：考察

$${n\brace m}_*=m{n+1\brace m}_*+{n+1\brace m-1}_*$$

）

从而可以通过归纳得到对于任意序列 $g$：

$$\sum_{n\ge1}\dfrac{g_n}{n^k}z^n=\sum_{j\ge1}{k+2\brace j}_{*}z^jG^{(j)}(z)$$

其中 $G(z)$ 是 $\{g\}$ 的 OGF .

Zeta Series Transformations

对于正整数 $k$、序列 $\{f(n)\}$ 和序列 $\{g_n\}$，有：

$$\sum_{n\ge1}\dfrac{g_n}{f(n)^k}z^n=\sum_{j\ge1}{k+2\brace j}_{f^*}z^jG^{(j)}(z)$$

其中 $G(z)$ 是 $\{g\}$ 的 OGF，且

$${n+2\brace m}_{f^*}=\dfrac1{m!}\sum_{k=1}^m\dbinom mk\dfrac{(-1)^{m-k}}{f(m)^n}$$

当 $f$ 是多项式时直觉上可以得到 ${n\brace m}_{f^*}$ 是 ${n+1\brace m-t}$ 其中 $t=0\dots\deg f$ 的组合，进而可以推导出最终结论 .

不过具体展开过于繁琐，这里先放一放 . 如果有人能够得出简洁的证明望不吝赐教 .

（[2] 给出了 $g_n=1$ 和 $g_n=\frac{r^n}{n!}$ 情况的证明）

（这里还有一个疑点：如何把这个变换倒过来做）

Reference:

[0] Wikipedia, Generating function transformation
[1] Maxie D. Schmidt, Generating Function Transformations Related to Polylogarithm Functions and the $k$-Order Harmonic Numbers
[2] Maxie D. Schmidt, Zeta Series Generating Function Transformations Related to Generalized Stirling Numbers and Partial Sums of the Hurwitz Zeta Function
[3] Private conversation with APJifengc

（怎么全是这个 Maxie D. Schmidt）

感觉好多纷繁的知识啊，原来我是一只，酒醉的蝴蝶~