2024.1.1 闲话

元旦激光炮，发射！！！！！！

洛谷上 Master 了（？

把《游戏人生zero》补了，有点震撼的 . 不多评了，推个歌吧：

歌：THERE IS A REASON - 鈴木このみ .

今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 . 今年是闰年 .

furry

图 1：Neuro 建立 furry 政权 .

图 2：APJifengc 积极宣传 furry 思想 .

有什么流程比较短的 galgame 吗？

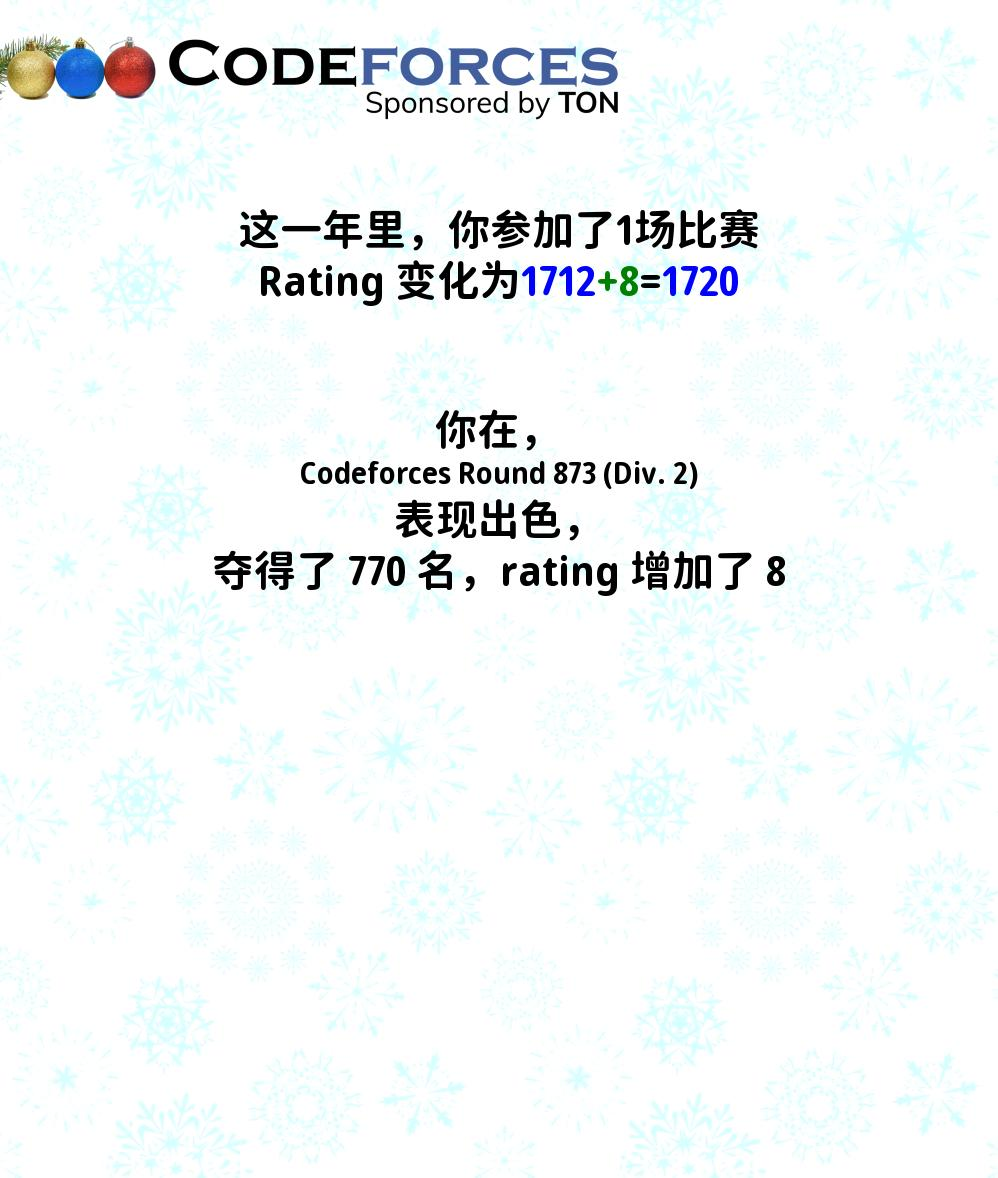
CF 年度报告

这啥玩意？

感觉那个闲话有些东西可能写得太不明显了，可能到后面我也会忘掉了，就像 Azune FFT 那个的人名含义一样 .

---

根据 EI 的某篇远古文章的教导某些素数（幂）处的统计内容也可以使用非积分的做法估计上界（通常是松的）：

问题：估计 \(\le n\) 的素数幂数量的上界 .

\[\begin{aligned}\mathrm{ans}&=\sum_{i=1}^{\log_2 n}\pi(\lfloor\sqrt[i]n\rfloor)\\&\sim\dfrac1{\ln n}\sum_{i=1}^{\log n}i\sqrt[i]n\end{aligned} \]

根据凸性可以得到后式的最大值为 \(n\)，从而有 \(\mathrm{ans}=O(n)\)（然而准确的界是 \(\mathrm{ans}=\Theta(\frac n{\ln n})\)）.

看起来对于任意正的增函数 \(f\) 都可以由此计算：

\[\sum_{i=1}^{\log n}f(i)\cdot\pi(\lfloor\sqrt[i]n\rfloor)=O(n) \]

直接积分算可能比较麻烦，这里如果界已经足够了的话用这种方法也是比较方便的 .

一个应用是暴力线性筛计算积性函数 Dirichlet 卷积的复杂度 .

因为 crimson000 有一个恋心的贺图那么我也放个恋心图，虽然和贺没关系 .

image