2023.12.22 闲话

突然发现好像我是信仰这种模拟赛模式的：

（此处应有一些问号或者同义短语）

哈哈哈我要学 lyndon word。。？？。？

觉

歌：クチナシの木が朽ちる前に - ox feat. 琴葉茜・葵 .

你们海鲜曲花活这么多的吗 .

---

抱歉放了一个这种文本在闲话里，觉得这种东西新开一个博也不好，放日记里也不好，就放闲话了（难道闲话就是你的垃圾桶吗？可能吧。所以为什么闲话要不显示在主页呢？）.

突然想放个目录（

目录

• Border Series
  • border 和 period
  • border 的结构
  • border 树链剖分
• Palindrome Series
  • 回文串的回文后缀
  • PAM 链剖分

Border Series

这不是一段 Border Theory 介绍文本，这里只会介绍一部分 Border 论的知识 .

border 和 period

定义一个字符串 \(S\) 的子串 \(T\subseteq S\) 是 \(S\) 的 border 当且仅当 \(T\neq S\) 且 \(T\) 既是 \(S\) 的前缀也是后缀 .

定义一个字符串 \(T\) 是 \(S\) 的周期 (period) 当且仅当存在正整数 \(k\) 使得 \(S\subseteq T^k\) .

由于某些深刻的原因，一个字符串 \(S\) 的最长 border \(b\) 和最小周期 \(p\) 有关系 \(b+p=|S|\) .

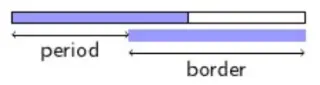
也可以了解一下 WPL，毕竟后面有用：若 \(p,q\) 都为字符串 \(S\) 的周期，且 \(p+q\le|S|\)，则 \(\gcd(p,q)\) 也是 \(S\) 的周期 .

border 的结构

定理：\(S\) 的所有长度不小于 \(\frac{|S|}2\) 的 border 长度构成等差数列 .

简要证明：假设两个 border 的长度分别为 \(b_1,b_2\)，其中 \(b_1\) 是最长 border .

考察对应的 period \(p_1,p_2\) 使得 \(p_1+b_1=p_2+b_2=|S|\)，则由 WPL 得 \(\gcd(p,q)\) 也是 period，从而存在长度为 \(n-\gcd(p_1,p_2)\) 的 border .

又 \(b_1\) 是最长 border，从而 \(\gcd(p_1,p_2)\ge p_1\)，也就是 \(p_1\mid p_2\)，从而可以导出等差数列 .

第二个定理：\(S\) 的所有 border 长度构成 \(O(\log|S|)\) 个等差数列 .

Cage：证明考虑切换 period 时，串长减半（？？？

简要证明：先把不小于长度一半的 border 分出来，然后取出最小 border \(T\subseteq S\)，可以通过讨论最小 period 和 \(\frac{|S|}4\) 的大小来导出 \(|T|\le\frac34|S|\)，从而每次问题缩小 \(\frac34\)，证明完毕 .

其实能证到 \(\lceil\log|S|\rceil\) .

border 树链剖分

在 border 树上考察 border 等差数列的结构，可以将其划分为若干个等差数列链，一个结点不断向上跳只会引发 \(O(\log n)\) 次切换，这就导出一种链剖分 .

例题：HNOI2019 JOJO .

Palindrome Series

回文串的回文后缀

注意到一个回文串的回文后缀也是它的 border，从而也可以构成 log 个等差数列 .

因为一节只有一句话不好，所以加个例题：

给一个字符串，每次查一个子串有多少种被分为两个回文子串的方法 .

建前缀后缀 PAM，枚举一侧等差数列的等价类 exgcd 解方程即可 .

时间复杂度带两个 log .

PAM 链剖分

注意 PAM 实际上是树而不是 DAG，所以链剖分是自然的 .

类似 border 树链剖分，对每个等差数列等价类划分为一条链，这样就得到了一种链剖分 .

一种常见应用是优化 DP，比如问划分为若干个回文串然后统计贡献什么的 .

例如我们现在要求字符串的回文划分数量，那么转移就是：

\[dp_i=\sum_{j\le i\land S[j:i]\in\mathbb P}dp_{j-1} \]

其中 \(\mathbb P\) 是回文串的集合 .

维护每个点到链顶的 \(dp\) 和，那么就可以和谐地转移所有信息了 .

详细说明及例题见 APJifengc 的博客 .